| Практическая работа № 1 (2-й семестр) «Векторы на плоскости и в пространстве» Решите задачу Треугольник АВС задан в прямоугольной системе координат пространства. Найдите:
| |||||||||
| № варианта | Координаты точки А | Координаты точки В | Координаты точки С | ||||||
| х | у | z | х | у | z | х | у | z | |
| | -1 | -3 | 1 | 2 | 4 | 4 | 6 | -1 | 4 |
| | 1 | -2 | 3 | 7 | 2 | -2 | 2 | 3 | 2 |
| | -3 | -3 | -1 | -2 | 3 | -1 | 3 | -2 | 3 |
| | 1 | 3 | 0 | 6 | -1 | -1 | -3 | 1 | -1 |
| | -4 | -2 | 2 | -3 | 3 | -3 | 5 | -3 | 3 |
| | 3 | -2 | -2 | -3 | -4 | 4 | 1 | 3 | -4 |
| | 3 | -1 | 2 | 2 | 1 | -2 | -2 | 7 | 1 |
| | -2 | -2 | -3 | 1 | -3 | -2 | -1 | 3 | -3 |
| | -2 | -3 | 1 | -3 | 2 | 3 | 2 | 4 | 2 |
| | 4 | 1 | -4 | 2 | -2 | 3 | 1 | 3 | -2 |
| | -2 | 1 | 4 | 0 | 2 | -4 | 3 | 1 | -1 |
| | -1 | 2 | -2 | 3 | 1 | 1 | -1 | 0 | 1 |
| | -1 | 3 | -1 | 1 | -2 | 3 | 0 | 3 | -3 |
| | -3 | -1 | -1 | 0 | -1 | -1 | 2 | 1 | 1 |
| | 4 | 1 | -3 | -3 | 2 | 0 | -2 | 0 | -4 |
| | -2 | -3 | 4 | 1 | -3 | 2 | 2 | 0 | 3 |
| | -2 | -2 | -2 | 1 | 1 | -2 | -3 | 0 | 3 |
| | 3 | -1 | -2 | 1 | 2 | 2 | 1 | 1 | -2 |
| | 3 | 2 | 3 | -1 | 3 | -3 | -4 | 0 | -2 |
| | -4 | -2 | 3 | 0 | -3 | 1 | 3 | -1 | 4 |
| | 1 | 4 | -4 | 1 | -1 | -1 | 4 | -1 | -1 |
| | 3 | 2 | 1 | 3 | -2 | 1 | 2 | 1 | -2 |
| | -1 | 3 | 3 | -1 | -3 | -3 | 3 | -3 | -3 |
| | 0 | -1 | -1 | 0 | 1 | 1 | -1 | 1 | 1 |
| | 2 | 3 | 0 | 2 | 1 | -4 | 3 | -4 | 1 |
| | -2 | -4 | 2 | -2 | 2 | 3 | -4 | 3 | 2 |
| | 2 | 1 | -2 | 2 | 3 | 3 | 1 | 3 | 3 |
| | -3 | -3 | 2 | -3 | -1 | -2 | -3 | -2 | -1 |
| | 1 | 2 | -3 | 1 | 1 | -2 | 2 | -2 | 1 |
| | -4 | -2 | 1 | -4 | -3 | 4 | -2 | 4 | -3 |
| | 3 | 2 | 8 | -3 | 2 | 3 | -1 | -2 | 1 |
| | 4 | -3 | 5 | 2 | -3 | -2 | -2 | -2 | 3 |
| | -2 | 1 | 2 | 1 | 1 | -2 | -3 | 3 | -1 |
| | -2 | -4 | 4 | -3 | -4 | 3 | 1 | 3 | 0 |
| | 3 | 3 | 1 | 2 | 3 | 3 | 1 | -4 | 2 |
В
 Образец оформления и выполнения практической работы.
Образец оформления и выполнения практической работы.
Задача. Дано. АВС – треугольник, А(2;-3;0), В(4;3;6), С(0;-1;-2).
Найти: М2 М1



координаты всех векторов
М0
периметр треугольника АВС
косинус всех углов треугольника;
С
А
координаты середин всех сторон треугольника;
М3
координаты центра тяжести треугольника АВС.
Решение.
По формуле
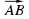 (хВ - хА; уВ - уА; zВ - zА) = (4-2; 3-(-3); 6-0).получили
(хВ - хА; уВ - уА; zВ - zА) = (4-2; 3-(-3); 6-0).получили
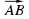 (2; 6; 6),
(2; 6; 6), 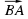 (-2; -6; -6)
(-2; -6; -6)
Аналогично. 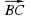 (-4; -4; -8)
(-4; -4; -8)  (4; 4; 8)
(4; 4; 8)
 (-2; 2; -2)
(-2; 2; -2)  (2; -2; 2)
(2; -2; 2)
Периметр ∆ АВС – есть сумма длин сторон этого треугольника.
По формуле  ; получаем
; получаем  =
=  =
= 
Аналогично  =
=  = 9,8;
= 9,8;  =
=  = 3,5
= 3,5
Р∆ABC =  +
+  +
+  =
=  + 9,8 + 3,5 = 22 (ед.)
+ 9,8 + 3,5 = 22 (ед.)
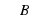 находится между векторами ВА и ВС;
находится между векторами ВА и ВС; 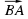

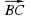 =
= 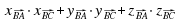
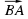

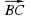 = (-2)
= (-2)  (-4) + (-6)
(-4) + (-6) (-4) + (-6)
(-4) + (-6) (-8) = 80;
(-8) = 80;
 находится между векторами АВ и АС;
находится между векторами АВ и АС; 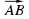

 =
= 
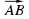

 = 2
= 2 (-2) + 6
(-2) + 6  2 + 6
2 + 6 (-2) = - 4;
(-2) = - 4;
 находится между векторами СА и СВ;
находится между векторами СА и СВ; 

 =
=


 = 2
= 2 4 + 4
4 + 4 (-2) + 6
(-2) + 6 2 = 16;
2 = 16;
Найдём значение по формуле
=
=
= 0,9;
Аналогично найдём =
=
= - 0,13;
=
= 0,47;
Координаты середин сторон находим по формулам M3 ;
Координаты середины стороны АВ найдём по формулам M1 ;
Середина стороны АВ – М1 () = (3; 0; 3); М1 (3; 0; 3)
Середина стороны ВС – М2 () = (2; 1; 2); М2 (2; 1; 2);
Середина стороны АС – М3 = (1; -2; -1); М3 (1; -2; -1)
5. Центр тяжести треугольника находится в точке пересечения его медиан. Все медианы треугольника пересекаются в одной точке М0, которая делит каждую медиану в отношении , считая от вершины. Рассмотрим медиану с удобными для решения координатами её концов. В нашей задаче – это медиана СМ1 . Точка М0 делит эту медиану в отношении 2:1, начиная от вершины, т.е.
=
= 2 поэтому в следующих формулах
, С(0;-1;-2), М1 (3; 0; 3)
M0 = = =
Если выбрана другая медиана, то формулы выглядят так:
Для медианы АМ2 M0, где , А(2;-3;0), М2 (2; 1; 2);
Для медианы ВМ3 M0, где , В(4;3;6), М3 (1; -2; -1);
Для всех случаев ответ должен получиться один и тот же: M0
ОТВЕТ: 1. и. 4. См. решение; 2. Р∆ABC = 22 (ед.)
3. =
0,9;
= - 0,13;
= 0,47; 5. M0



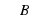 находится между векторами ВА и ВС;
находится между векторами ВА и ВС;