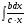Министерство общего и профессионального образования
Свердловской области.
ГБПОУ СО «ИГРТ».
ПОДГОТОВКА К ЭКЗАМЕНУ
По дисциплине «Математика»
для студентов первого курса дневного отделения
(Технические специальности).
Рассмотрено Утверждаю
цикловой комиссией Зам. директора по УВР
Председатель ____________/И.А.Фот/
_________/Н.С. Жукова/
Составил
Преподаватель математики Л.Н. Фот
Пояснительная записка
Максимальное количество часов за год - 366 часов, в том числе: аудиторных - 244 часов,
самостоятельная работа студентов - 122 часов.
Итоговая аттестация проводится в виде экзамена и включает в себя задания по темам.
Тема 1.1. Действительные числа. Уравнения, неравенства, системы
Тема 1.2. Функциональная зависимость
Тема 1.3. Показательная, логарифмическая и степенная функции. Уравнения и неравенства
Тема 1.4. Тригонометрические функции
Тема 2.1. Прямая и плоскость в пространстве, их взаимное расположение.
Тема 2.2. Геометрические тела, их объёмы и поверхности.
Тема 2.3. Векторы на плоскости и в пространстве.
Тема 3.1. Производная функции. Приложения производной.
Тема 3.2. Дифференциал функции.
Тема 4.1. Неопределенный и определенный интеграл.
Критерии оценки.
В экзаменационном билете 9 заданий. За каждое правильно выполненное задание, в зависимости от уровня сложности, студент получает определенное количество баллов. Общее количество баллов за работу – 57.
Из заданий, имеющих несколько примеров, достаточно решить один (по выбору студента).
На положительную оценку необходимо правильно решить задания и набрать не менее 40 баллов.
Шкала перевода баллов.
50-и более баллов – «отлично»
45-49 баллов – «хорошо»
40-44 баллов – «удовлетворительно»
Менее 40 баллов – «неудовлетворительно»
Задание 1 (2 балла)
Исследуйте и решите систему уравнений методом Крамера.
Задание 2 (6 баллов)
Решите уравнение и неравенство:
Для всех вариантов, а = n, b = n + 1, c = n + 2, где n – номер вашего варианта
2.1.  (3 балла)
(3 балла)
2.2.  (3 балла)
(3 балла)
Задание 3 (4 баллов)
Решите тригонометрические уравнения:
3.1.  (2 балла); 3.2.
(2 балла); 3.2.  . (2 балла).
. (2 балла).
Задание 4 (10 баллов)
Исследуйте функцию по правилу, с использованием первой и второй производной и постройте её график.
 , где
, где 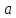 - № варианта.
- № варианта.
(п.п. 1,2,5,6 – по функции; 7,8 – по 1-й производной; 9,10 – по 2-й производной;
11 – график.
Исследовать по функции и первой производной – 4 балла,
исследовать по второй производной – 3 балла,
построить схематичный график функции – 3 балла.
Задание 5 (8 баллов)
Решите задачи:
Для всех вариантов: n – номер вашего варианта
а = n Н = n + 5
5.1. В правильной треугольной призме сторона основания равна 2а, высота равна Н. Найдите полную поверхность и объем этой призмы. (3 балла)
5.2. Найдите полную поверхность и объём конуса, если диметр основания равен 2а см., образующая наклонена к плоскости основания под углом 60о. (5 баллов)
Задание 6 (5 баллов)
Найдите производные функций
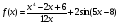 ;
;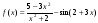 ;
;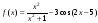 ;
;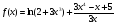 ;
;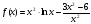 ;
;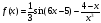 ;
;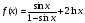 ;
;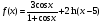 ;
;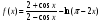 ;
;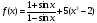
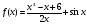 ;
;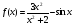 ;
;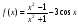 ;
;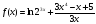 ;
;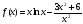 ;
;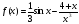 ;
;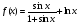 ;
;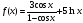 ;
;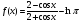 ;
;
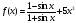 Задание 7 (10 баллов)
Задание 7 (10 баллов)Вычислите интегралы:
Для всех вариантов a = n, b = n + 1, c = n + 2, где n – номер вашего варианта.
7.1. Вычислите интеграл, применяя формулы и правила интегрирования (по 1 баллу за каждый пример)
а)
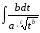 ; б)
; б) 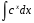 ; в)
; в) 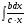
7.2.Вычислите интеграл, применяя преобразование подынтегральной функции и формулы и правила интегрирования (3 балла)
7.3. Вычислите интеграл, применяя правило
(по 2 балла за каждый пример)
а)
; б)
Задание 8 (5 баллов)
Найдите неизвестные элементы треугольника по заданным элементам
-
Вар.
№
Прямоугольный треугольник АВС
Вар.
№
Косоугольный треугольник АВС
a
b
с
А
В
S
а
b
с
А
В
С
S
9.35
65010′
370
86037′
50030′
10,24
32,12
510
317
76010′
6,37
4020′
87
65
750
3,65
50010′
450
87050′
10050′
0,2954
25037′
225
800
36040′
9,53
65015′
350
86036′
50050′
10,20
32,10
520
330
76010′
6,73
5020′
78
56
800
3,46
52010′
450
87030′
10040′
0,30
25040′
220
800
36048′
Задание 9 (7 баллов)
Решите задачу
Дано. АВС – треугольник. Найдите:
Координаты всех векторов (1 балл);
Периметр треугольника АВС с точностью до 0,01 (2 балла);
Косинусы внутренних углов треугольника АВС с точностью до 0,01 (2 балла)
Координаты центра тяжести треугольника АВС. (2 балла);
-
№ варианта
Координаты точки
А
Координаты точки
В
Координаты точки
С
х
у
х
у
х
у
-1
-3
2
4
6
-1
1
-2
7
2
2
3
-3
-3
-2
3
3
-2
1
3
6
-1
-3
1
-4
-2
-3
3
5
-3
3
-2
-3
-4
1
3
3
-1
2
1
-2
7
-2
-2
1
-3
-1
3
-2
-3
-3
2
2
4
4
1
2
-2
1
3
-2
1
0
2
3
1
-1
2
3
1
-1
0
-1
3
1
-2
0
3
-3
-1
0
-1
2
1
4
1
-3
2
-2
0
-2
-3
1
-3
2
0
-2
-2
1
1
-3
0
3
-1
1
2
1
1
3
2
-1
3
-4
0
-4
-2
0
-3
3
-1
Основные формулы и рекомендации к выполнению заданий. (1 курс)
К заданию № 1 Исследовать и решить систему линейных уравнений.
Решить систему методом Крамера
Метод Крамера: 1) Составляем главный определитель системы
,
если
, то система имеет единственное решение
;
2) Составляем вспомогательные определители по х и по у:
и
Ответ: Система имеет единственное решение
.
-
К заданию № 2. Логарифмическая и показательная функции.
Показательная функция.
Формулы.
Показательные уравнения.
, решить полученное ур-ние.
Записать Ответ.
Показательные неравенства
если
, знак не меняется,
если
, знак меняется,
Логарифмическая функция.
Формулы.
Логарифмические уравнения.
, решить ур-ние.
Проверить корни в ОДЗ: и записать Ответ.
Логарифмические неравенства.
если
, знак не меняется,
, где b
a
a ≠1;
если
, знак меняется
-
К заданию № 3 Тригонометрические функции.
Формулы.
Тригонометрические уравнения.
;
,
x=
если
то x =
если
то x =
+
,
если
то x=
+
,
x=
если
то x =
+
.
если
то x =
если
то x =
+
;
, где
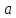 - любое число
- любое число
x=
если
то x =
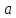 - любое число
- любое число
x=
если
то x =
+
.
К заданию № 4. Приложение производной.
План исследования функции y = f(x)
По функции: п/п 1;2;и 5;6 – корни знак ф-ции.
О.О.Ф. – х
… 2. М.З.Ф. – у
…
5.6. Ф-цию приравнять к нулю, f(x) = 0, найти корни – x1,x2, x3; расположить их в порядке возрастания на числовой оси; (числ. ось разбилась на интервалы). Определить знак функции в каждом полученном интервале.
По производной первого порядка: п/п 7;8 – монотонность, экстремумы ф-ции.
Найти производную первого порядка y′ = f ′(x);
Приравнять производную к нулю f ′(x) = 0, найти корни (стационарные точки 1-го рода) x4,x5;
Расположить точки в порядке возрастания на числовой оси; (числ. ось разбилась на интервалы).
Определить знак производной в каждом полученном интервале:
- там, где y′
, там y = f(x) возрастает
- там, где y′
, там y = f(x) убывает
максимум, ymax = f(x4), M1(x4; f(x4)) точка максимума
- в стационарной точке, в которой знак производной меняется с
на
, функция имеет минимум, ymin = f(x5), M2(x5; f(x5)) точка минимума
По производной второго порядка: п/п 9;10 – выпуклость кривой и точки перегиба.
Найти производную второго порядка y′′ = f ′′ (x);
Приравнять производную к нулю f′′(x) = 0, найти корни (стационарные точки второго рода) x6;
Расположить точки в порядке возрастания на числовой оси; (числ. ось разбилась на интервалы).
Определить знак производной в каждом полученном интервале:
- там, где y′
, там y = f(x) вогнута,
- там, где y′
, там y = f(x) выпукла,
-.в стационарной точке, в которой знак второй производной меняется, функция имеет перегиб
уперегиба = f(x6); M3(x6; f(x6)) точка перегиба;
п. 11. Построить график функции в системе координат.
-
К заданию № 5. Стереометрия
Многогранники
Призма
Пирамида
Усечённая пирамида
Sполн= Sбок+2
Sосн
Sполн= Sбок+ Sосн
Sполн.ус.пир.= Sбок+ Sн+ Sв
Sбок =
боковых граней.
Sбок =
боковых граней.
Sбок =
боковых граней.
V призмы = Sосн
,
где
призмы
V пирам. = 1/3
Sосн
,
где
пирамиды.
Полезно знать: 1).
, где a, b – стороны треугольника,
- угол между сторонами a, b. 2). S∆ABC =
·a·h, 3). Sпараллелограмма = a·h, 4). Sромба =
m
n, где m и n – длины диагоналей ромба
-
Круглые тела
Прямой круговой цилиндр
Прямой круговой конус
Усечённый конус
Sбок=2
Sбок=
Sбок=
(
)
Sполн=Sбок+2Sосн=2
+ 2
=
(r +
)
Sполн=Sбок+Sосн=
+
=
(
+
)
Sполн. = Sбок + Sв + Sн
V=
V=1/3
V=1/3
(Sв +
+ Sн),
где Sв
; Sн
Шар. Сфера.
Vш = 4/3
; Sш=4
-
К заданию № 8 Решение треугольников.
Прямоугольный треугольник
Косоугольный треугольник
=
;
=
=
;
=
Теорема Пифагора
S∆ABC =
·a·b
Теорема синусов
Теорема косинусов
где a, b – стороны треугольника,
- угол между сторонами a, b.
-
Значения тригонометрических некоторых углов.
00
300
450
600
900
1800
2100
2400
2700
3000
3300
3600
0
sin
0
1
0
1
0
cos
1
0
1
0
1
tg
0
1
Не сущ.
0
Не сущ.
0
ctg
Не сущ.
1
0
Не сущ.
0
Не сущ.
-
К заданию № 6
К заданию № 7
Вычисление производной функции.
Вычисление интегралов.
(с) ' = 0 где с – const
(x) ' = 1
(cu) ' = c
u)'
(u ± v)' = u' ± v'
(u
v)' = u'v+v'u
' =
(um)' = m
u';
(au)' = au
lna
u'
(eu)' = eu
u'
(log a u)' =
(sin u)' = cos u
u'
(cos u)' =
sin u
u'
(tg u)' =
(ctg u)' =
(arcsin u)' =
(arccos u)' =
(arctg u)' =
(arcctg u)' =
∫ dx = x + C,
∫ xm dx =
+C; где m ≠
1
= ln
+ C
∫ax dx =
+ C (a0, a ≠1).
∫ex dx = ex + C.
∫sin x dx =
cos x + C.
∫cos x dx = sin x + C.
= tg x + C.
=
ctg x + C
. = arcsin x + C.
. =
arccos x + C.
= arctg x + C
=
arcctg x + C
∫ df(x) = f(x)+C,
∫k
f(x)d x = k
∫f(x)
dx , где k =const,
∫(f(x) +
(x)) dx = ∫f(x)dx + ∫
g(x)dx.
∫
f(kx +b)dx =
F(kx +b)
, где k ≠
1 и F(kx +b) – первообразная для f(kx +b)
-
К заданию № 9 Векторы.
А (х1;у1)
В (х2;у2)
С (х3;у3)
М0
АМ1
ВМ2 = М0 , где М0
– центр тяжести
АВС
на плоскости
в пространстве
( х2
х1; у2
у1 )
( х2
х1; у2
у1; z2
z1)
M2
M2
M0, где
M0
Скалярное произведение векторов.
, где
- угол между векторами.
=
=


















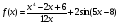 ;
;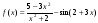 ;
;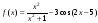 ;
;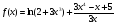 ;
;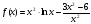 ;
;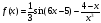 ;
;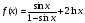 ;
;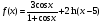 ;
;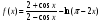 ;
;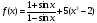
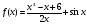 ;
;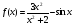 ;
;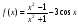 ;
;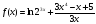 ;
;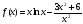 ;
;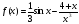 ;
;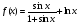 ;
;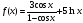 ;
;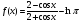 ;
;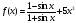 Задание 7 (10 баллов)
Задание 7 (10 баллов)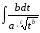 ; б)
; б) 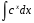 ; в)
; в)