
Готовимся к ОГЭ
Урок - игра

Каталог задач
1
2
3
4
5
6
7
Утверждения
Площадь
Окружность
Углы
4
5
7
1
3
6
2
4
7
5
6
3
2
1
1
6
5
4
3
2
7
Марченко И.Л.

Задача 1
1) В параллелограмме есть два равных угла.
2) Каждая из биссектрис равнобедренного треугольника является его медианой.
3) Площадь прямоугольного треугольника равна произведению длин его катетов.
1
Марченко И.Л.

Задача 2
1) Боковые стороны любой трапеции равны.
2) Площадь прямоугольника равна произведению длин его смежных сторон.
3) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
2
Марченко И.Л.

Задача 3
1) Диагонали равнобедренной трапеции равны.
2) Если три угла одного треугольника равны соответственно трём углам другого треугольника, то такие треугольники равны.
3) Тангенс любого острого угла меньше единицы.
1
Марченко И.Л.

Задача 4
1) Если угол острый, то смежный с ним угол также является острым.
2) Если диагонали параллелограмма перпендикулярны, то этот параллелограмм является ромбом.
3) Касательная к окружности параллельна радиусу, проведённому в точку касания.
2
Марченко И.Л.

Задача 5
1) Косинус острого угла прямоугольного треугольника равен отношению гипотенузы к прилежащему к этому углу катету.
2) Диагонали ромба перпендикулярны.
3) Существуют три прямые, которые проходят через одну точку.
23
Марченко И.Л.

Задача 6
1) Две различные прямые, перпендикулярные третьей прямой, параллельны.
2) Если диагонали выпуклого четырёхугольника равны и перпендикулярны, то этот четырёхугольник является квадратом.
3) Все углы ромба равны.
1
Марченко И.Л.

Задача 7
1) Вертикальные углы равны.
2) Две прямые, параллельные третьей прямой, перпендикулярны.
3) Диагонали любого прямоугольника делят его на четыре равных треугольника.
1
Марченко И.Л.

Задача 1
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
14
Марченко И.Л.
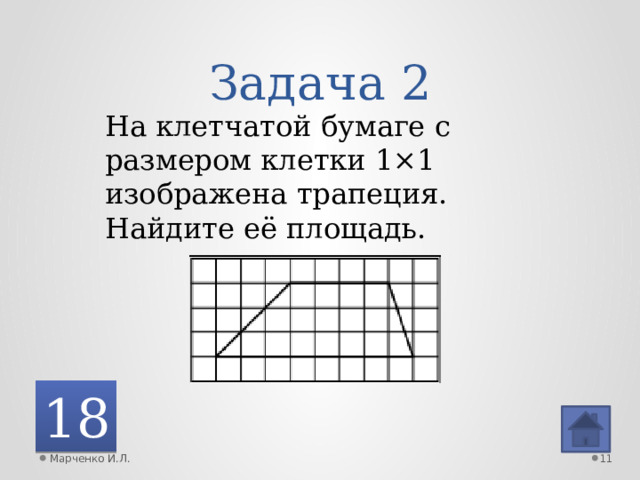
Задача 2
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
18
Марченко И.Л.
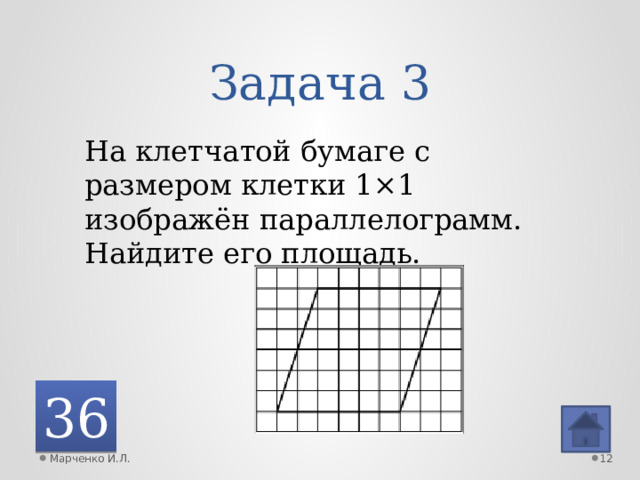
Задача 3
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
36
Марченко И.Л.

Задача 4
Два катета прямоугольного треугольника равны 6 и 13. Найдите площадь этого треугольника.
39
Марченко И.Л.

Задача 5
Периметр квадрата равен 88. Найдите площадь этого квадрата.
484
Марченко И.Л.

Задача 6
Найдите площадь ромба, если его диагонали равны 8 и 6.
24
Марченко И.Л.

Задача 7
Найдите площадь параллелограмма, изображённого на рисунке.
100
Марченко И.Л.
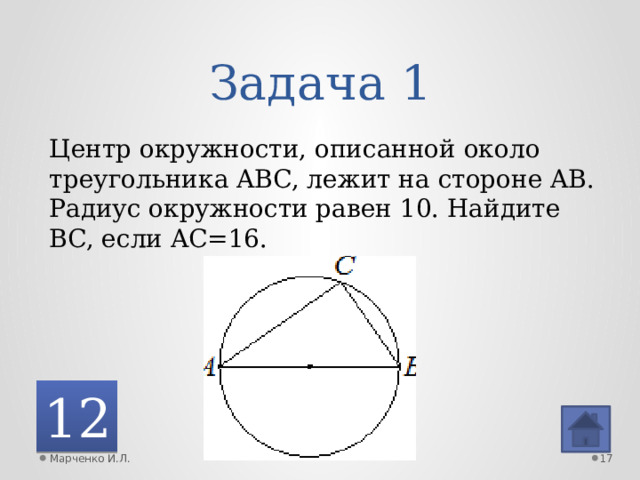
Задача 1
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 10. Найдите BC, если AC=16.
12
Марченко И.Л.

Задача 2
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если
угол BAC равен 53°. Ответ дайте в градусах.
37°
Марченко И.Л.

Задача 3
Отрезки AC и BD — диаметры окружности с центром в точке O. Угол ACB равен 54°. Найдите угол AOD. Ответ дайте в градусах.
72°
Марченко И.Л.

Задача 4
В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 88°. Найдите угол ACB. Ответ дайте в градусах.
46°
Марченко И.Л.

Задача 5
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 134°, угол CAD равен 81°. Найдите угол ABD. Ответ дайте в градусах.
53°
Марченко И.Л.

Задача 6
Касательные в точках A и B к окружности
с центром в точке O пересекаются под углом 88°. Найдите угол ABO. Ответ дайте в градусах.
44°
Марченко И.Л.

Задача 7
Треугольник ABC вписан в окружность с центром
в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 47°. Ответ дайте в градусах.
94°
Марченко И.Л.

Задача 1
Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 15°. Ответ дайте в градусах.
30°
Марченко И.Л.

Задача 2
Сумма двух углов равнобедренной трапеции равна 50°. Найдите больший угол этой трапеции. Ответ дайте
в градусах.
155°
Марченко И.Л.
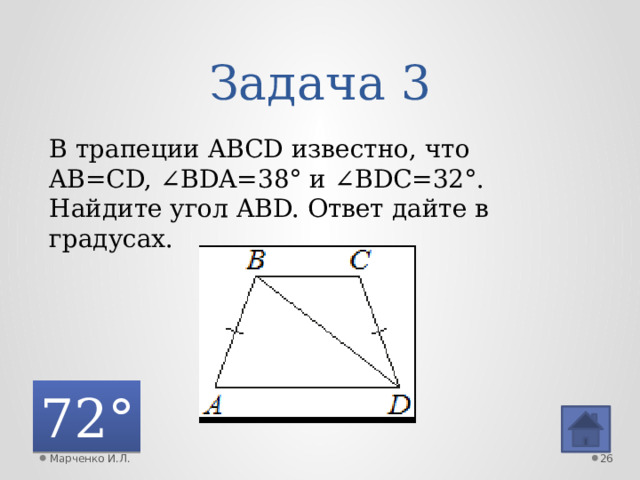
Задача 3
В трапеции ABCD известно, что AB=CD, ∠BDA=38° и ∠BDC=32°. Найдите угол ABD. Ответ дайте в градусах.
72°
Марченко И.Л.

Задача 4
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 47° и 15° соответственно. Ответ дайте в градусах.
118°
Марченко И.Л.
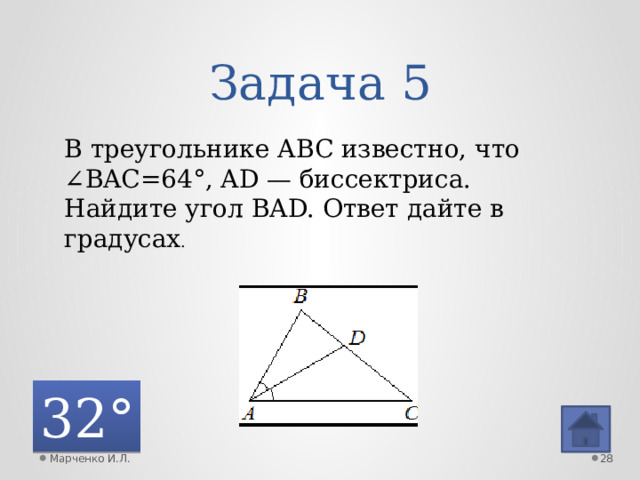
Задача 5
В треугольнике ABC известно, что ∠BAC=64°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах .
32°
Марченко И.Л.
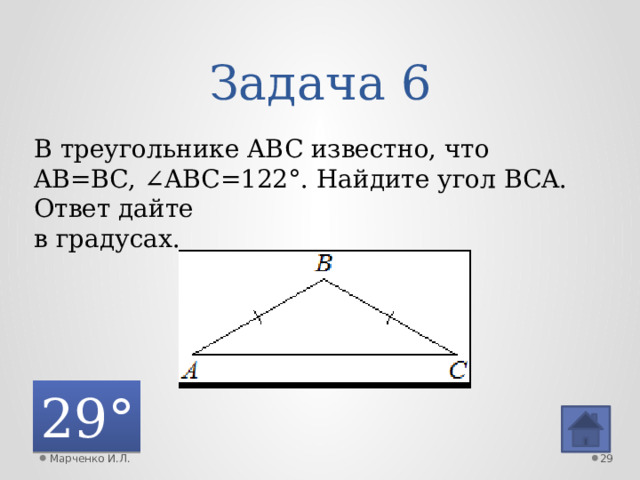
Задача 6
В треугольнике ABC известно, что AB=BC, ∠ABC=122°. Найдите угол BCA. Ответ дайте
в градусах.
29°
Марченко И.Л.

Задача 7
Один из острых углов прямоугольного треугольника равен 68°. Найдите его другой острый угол. Ответ дайте в градусах.
22°
Марченко И.Л.







