Тесты по геометрии «Сумма углов многоугольника»
Вариант 1
1. Угол, с вершиной в центре окружности, называется
А) центральным В)вписанным С)прямым Д)развернутым
2. Окружность называется описанной около многоугольника, если:
а) все его стороны касаются окружности
б) все его стороны имеют общие точки с окружностью
с) все его вершины лежат на окружности
д) все его стороны являются отрезками касательных к данной окружности
3. Какие из перечисленных многоугольников являются правильными?
а)равнобедренный треугольник; б)квадрат; в)ромб; г)прямоугольник
4. Сумма углов выпуклого многоугольника равна
а)180º (n – 3). б)180º (n – 2). С)360º.
5. Чему равна сумма внутренних углов выпуклого семиугольника?
А)1080°; В) 720°; С)900; Д)540.
6.Сколько сторон имеет выпуклый многоугольник, каждый угол которого равен 108 град.?
а)5; б)7; в)10; г)6.
7.Точка О является центром правильного треугольника ABC. Чему равна его сторона, если радиус описанной окружности равен 6 см?
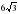 см; б)
см; б)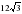 см; С)
см; С)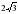 см; д)
см; д)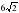 см.
см.
8. В окружность вписан правильный шестиугольник с периметром 18 см. Найти радиус окружности.
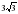 см; б)3 см; с)6 см; д)
см; б)3 см; с)6 см; д)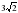 см.
см.
9. Сторона одного квадрата в три раза больше стороны другого квадрата. Как относятся радиусы окружностей, описанных около них и вписанных в них?
9 : 1; б)3 : 1; с)3 : 2 д)3:9
10. Периметр равностороннего треугольника равен 63 см. Найдите радиус описанной окружности.
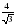 см; б)
см; б)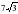 см; с)2 см; д)4 см.
см; с)2 см; д)4 см.
11.Около квадрата описана окружность и в квадрат вписана окружность. Найдите радиус вписанной окружности, если радиус описанной окружности равен  см.
см.
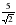 см; б)10 см; с)
см; б)10 см; с)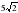 см; д)5 см.
см; д)5 см.
12. Внешний угол правильного многоугольника меньше внутреннего угла на 140°. Найдите сумму углов данного многоугольника.
2400°; б)3060°; с)2880°; д)2700°.
13. Найдите площадь правильного треугольника со стороной а.
а) а2√3 б) а2√3 / 4 с) а2√3 / 2 д) а2√3 / 3
14. В окружность радиуса R вписан правильный шестиугольник. Найдите его площадь.
а) √3 R2 б) 2√3 R2 с 3√3 R2 д (3√3/2)R2
15. Вокруг правильного шестиугольника описана окружность. В этот шестиугольник также вписана окружность. Чему равно отношение радиусов этих окружностей?
а) √3 : 1
б) 2 : √3
с) √2 : 1
д) √3 : √2
16. укажите формулу для вычисления радиуса описанной окружности около треугольника:
А) 
17. укажите формулу для вычисления радиуса описанной окружности около четырехугольника:
А) 
18. укажите формулу для вычисления радиуса описанной окружности около шестиугольника:

19. Чему равна площадь равностороннего треугольника со стороной 6 см?
а) 9 см2 б) 9√3 см2 с) 18 см2 д) 18√3 см2
20. В любом вписанном четырехугольнике:
а) суммы смежных сторон равны
б) суммы противоположных сторон равны
с) сумма соседних углов равна 180°
д) сумма противоположных углов равна 180°
Вариант 2.
1. Вписанный угол, который опирается на полуокружность, называется
А) острым б)развернутым с)центральным д)прямым
2. Угол, градусная мера которого, равна половине дуги на которую он опирается, называется
А)центральным б)вписанным с)развернутым д)прямым
3.Окружность называется вписанной в многоугольник, если:
а) все его стороны касаются окружности
б) все его вершины лежат на окружности
с) все его стороны имеют общие точки с окружностью
д) все его стороны являются отрезками касательных к данной окружности
4.Чему равна сумма внутренних углов выпуклого десятиугольника?
1620°; б)1260°; с)1080°; д)1440°.
5.Сколько углов имеет выпуклый многоугольника, каждый угол которого равен 135°?
6; б)12; с)8; д)10.
6.Внутренние углы выпуклого десятиугольника равны. Найти внешний угол.
36°; б)72°; с)18°;
7.Треугольник DBC – правильный. Чему равна сторона треугольника, если радиус вписанной окружности равен 5 см?
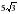 см; б)
см; б)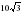 см; с)10 см; д)
см; с)10 см; д)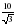 см.
см.
8.Окружность вписана в правильный шестиугольник с периметром 180 см. Найти радиус окружности.
4,5 см; б)9 см; с)6 см; д)
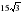 см
см
9.Периметр квадрата 120 см. Найдите радиус описанной окружности.
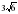 см; б)
см; б)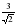 см; с)
см; с)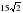 см; д)3 см.
см; д)3 см.
10.Около правильного треугольника описана окружность радиусом 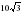 см Найдите радиус окружности, вписанной в этот треугольник.
см Найдите радиус окружности, вписанной в этот треугольник.
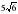 см; б)
см; б)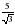 см; с)
см; с)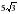 см д)10 см.
см д)10 см.
11.Внешний угол правильного многоугольника на 144° меньше внутреннего угла. Найдите сумму углов данного многоугольника
3600°; б)3240°; с)3060°; д)3420°
12.Найдите углы правильного десятиугольника.
а) 144° б) 150° с) 156° д) 162°
13.Вокруг правильного шестиугольника описана окружность. В этот шестиугольник также вписана окружность. Чему равно отношение радиусов этих окружностей?
а) √3 : 1 б) 2 : √3 с) √2 : 1 д) √3 : √2
14.В любом вписанном четырехугольнике:
а) суммы смежных сторон равны
б) суммы противоположных сторон равны
с) сумма соседних углов равна 180°
д) сумма противоположных углов равна 180°
15.Укажите формулу для вычисления радиуса вписанной окружности в треугольника:
А) 
16. Укажите формулу для вычисления радиуса вписанной окружности в четырехугольника:

17. Укажите формулу для вычисления радиуса вписанной окружности в шестиугольника:

18.Какие из перечисленных многоугольников являются правильными?
а)равнобедренный треугольник; б)квадрат; в)ромб; г)прямоугольник
19. Сумма углов выпуклого многоугольника равна
а)180º (n – 3). б)180º (n – 2). С)360º.
20. Чему равна сумма внутренних углов выпуклого семиугольника?
А)1080°; В) 720°; С)900; Д)540.
Вариант 3.
1.Радиус окружности, вписанной в правильный шестиугольник, равен 2 см. Вычисли площадь шестиугольника
А) 8√3 б)4 с))4√3 д)8
2.Вычисли радиус окружности, описанной около равностороннего треугольника, если его сторона равна 7√3 см.
А)7√3 б)7 в)10,5 с)3,5√3 д)3,5
3.Сторона равностороннего треугольника равна 10√3мм. Вычисли площадь треугольника;
А) 6 б) 75
б) 75 с) 10 д) 25
с) 10 д) 25
4.Вписанный угол, который опирается на полуокружность, называется
А) острым б)развернутым с)центральным д)прямым
5. Найдите углы правильного десятиугольника.
а) 144° б) 150° с) 156° д) 162°
6.Вокруг правильного шестиугольника описана окружность. В этот шестиугольник также вписана окружность. Чему равно отношение радиусов этих окружностей?
а) √3 : 1 б) 2 : √3 с) √2 : 1 д) √3 : √2
7.В любом вписанном четырехугольнике:
а) суммы смежных сторон равны
б) суммы противоположных сторон равны
с) сумма соседних углов равна 180°
д) сумма противоположных углов равна 180°
8.Треугольник DBC – правильный. Чему равна сторона треугольника, если радиус вписанной окружности равен 5 см?
А)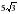 см; б)
см; б)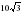 см; с)10 см; д)
см; с)10 см; д)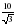 см.
см.
9.Окружность вписана в правильный шестиугольник с периметром 180 см. Найти радиус окружности.
А)4,5 см; б)9 см; с)6 см; д)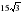 см
см
10.Около правильного треугольника описана окружность радиусом 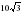 см Найдите радиус окружности, вписанной в этот треугольник.
см Найдите радиус окружности, вписанной в этот треугольник.
А)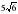 см; б)
см; б)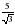 см; с)
см; с)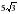 см д)10 см.
см д)10 см.
11.Периметр квадрата 120 см. Найдите радиус описанной окружности.
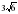 см; б)
см; б)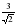 см; с)3 см; д).
см; с)3 см; д). 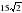 см
см
12.Вокруг правильного шестиугольника описана окружность. В этот шестиугольник также вписана окружность. Чему равно отношение радиусов этих окружностей?
а) √3 : 1 б) √3 : √2 с) √2 : 1 д) 2 : √3
13. Укажите формулу для вычисления радиуса вписанной окружности в четырехугольника:

14.В любом вписанном четырехугольнике:
а) суммы смежных сторон равны
б) суммы противоположных сторон равны
с) сумма соседних углов равна 180°
д) сумма противоположных углов равна 180°
15. Укажите формулу для вычисления радиуса вписанной окружности в шестиугольника:

16.Укажите формулу для вычисления радиуса вписанной окружности в треугольника:
А) 
17.Чему равна сумма внутренних углов выпуклого десятиугольника?
А)1620°; б)1260°; с)1080°; д)1440°.
18.Сколько углов имеет выпуклый многоугольника, каждый угол которого равен 135°?
А)6; б)12; с)8; д)10.
19.Внутренние углы выпуклого десятиугольника равны. Найти внешний угол.
А)36°; б)72°; с)18°;
20.Треугольник DBC – правильный. Чему равна сторона треугольника, если радиус вписанной окружности равен 5 см?
А)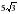 см; б)10 см; с)
см; б)10 см; с) 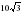 см; д)
см; д)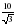 см.
см.
Вариант 4.
1. Чему равна сумма внутренних углов выпуклого семиугольника?
А)1080°; В) 720°; С)900; Д)540.
2.Сколько сторон имеет выпуклый многоугольник, каждый угол которого равен 108 град.?
а)5; б)7; в)10; г)6.
3.Точка О является центром правильного треугольника ABC. Чему равна его сторона, если радиус описанной окружности равен 6 см?
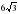 см; б)
см; б)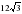 см; С)
см; С)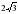 см; д)
см; д)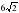 см.
см.
4. В окружность вписан правильный шестиугольник с периметром 18 см. Найти радиус окружности.
А)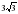 см; б)3 см; с)6 см; д)
см; б)3 см; с)6 см; д)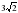 см.
см.
5. укажите формулу для вычисления радиуса описанной окружности около треугольника:
А) 
6. укажите формулу для вычисления радиуса описанной окружности около четырехугольника:
А)
7. укажите формулу для вычисления радиуса описанной окружности около шестиугольника:

8. Чему равна площадь равностороннего треугольника со стороной 6 см?
а) 9 см2 б) 9√3 см2 с) 18 см2 д) 18√3 см2
9. В любом вписанном четырехугольнике:
а) суммы смежных сторон равны
б) суммы противоположных сторон равны
с) сумма соседних углов равна 180°
д) сумма противоположных углов равна 180°
10. Угол, с вершиной в центре окружности, называется
А) центральным В)вписанным С)прямым Д)развернутым
11. Окружность называется описанной около многоугольника, если:
а) все его стороны касаются окружности
б) все его стороны имеют общие точки с окружностью
с) все его вершины лежат на окружности
д) все его стороны являются отрезками касательных к данной окружности
12. Какие из перечисленных многоугольников являются правильными?
а)равнобедренный треугольник; б)квадрат; в)ромб; г)прямоугольник
13. Сумма углов выпуклого многоугольника равна
а)180º (n – 3). б)180º (n – 2). С)360º.
14. Внешний угол правильного многоугольника меньше внутреннего угла на 140°. Найдите сумму углов данного многоугольника.
2400°; б)3060°; с)2880°; д)2700°.
15. Найдите площадь правильного треугольника со стороной а.
а) а2√3 б) а2√3 / 4 с) а2√3 / 2 д) а2√3 / 3
16. В окружность радиуса R вписан правильный шестиугольник. Найдите его площадь.
а) √3 R2 б) 2√3 R2 с 3√3 R2 д (3√3/2)R2
17. Вокруг правильного шестиугольника описана окружность. В этот шестиугольник также вписана окружность. Чему равно отношение радиусов этих окружностей?
а) √3 : 1
б) 2 : √3
с) √2 : 1
д) √3 : √2
18.Окружность вписана в правильный шестиугольник с периметром 180 см. Найти радиус окружности.
А)4,5 см; б)9 см; с)6 см; д)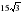 см
см
19.Около правильного треугольника описана окружность радиусом 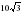 см Найдите радиус окружности, вписанной в этот треугольник.
см Найдите радиус окружности, вписанной в этот треугольник.
А)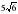 см; б)
см; б)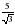 см; с)
см; с)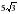 см д)10 см.
см д)10 см.
20.Периметр квадрата 122 см. Найдите радиус описанной окружности.
А)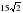 см; б)
см; б)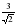 см; с)
см; с) 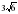 см; д)3 см.
см; д)3 см.



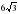 см; б)
см; б)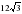 см; С)
см; С)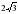 см; д)
см; д)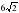 см.
см.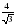 см; б)
см; б)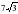 см; с)2 см; д)4 см.
см; с)2 см; д)4 см.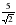 см; б)10 см; с)
см; б)10 см; с)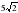 см; д)5 см.
см; д)5 см.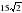 см
см



