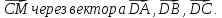Контрольная работа «Вектора в пространстве» 1 вариант
Часть 1
ABCDA1B1C1D1 –прямоугольный параллелепипед. Назовите вектор, равный сумме векторов
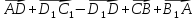 ;
;Изобразите систему координат в пространстве и A(-2; 3; -4).
Найдите длину вектора
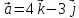 .
.Найдите координаты
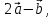 если
если 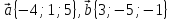 .
.Выясните, при каких значениях s и
 , вектора
, вектора 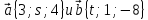 - коллинеарны.
- коллинеарны.Найдите координаты точки K, если A(0;3;4); В(1;4;4), а точка К-середина АВ.
Найдите скалярное произведение векторов
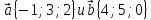 .
.
Часть 2
Найдите расстояние от точки P(-2; 3; 1) до оси абсцисс.
Вычислите угол между векторами
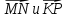 , если M(3;-2;4), N(4;-1;2), K(6;-3;2), P(7;-3;1).
, если M(3;-2;4), N(4;-1;2), K(6;-3;2), P(7;-3;1).В тетраэдре ABCD точка M – середина ребра BC. Выразите
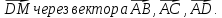
Точка A(2;-1;5), точка B симметрична точке A относительно начала координат, точка C симметрична точке B относительно плоскости Oxz. Найдите расстояние между точками A и С.
Контрольная работа «Вектора в пространстве» 2 вариант
Часть 1
ABCDA1B1C1D1 –прямоугольный параллелепипед. Назовите вектор, равный сумме векторов
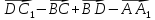 ;
;Изобразите систему координат в пространстве и A(1; -2; 4).
Найдите длину
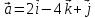 .
.Найдите координаты
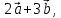 если
если 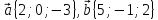 .
.Выясните, при каких значениях g и
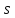 , вектора
, вектора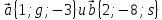 - коллинеарны.
- коллинеарны.Найдите координаты точки М, если А(3;-2;1); С(-1;2;2), а точка М-середина АС.
Найти скалярное произведение векторов
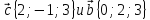 .
.
Часть 2
Найдите расстояние от точки F(-4; 2; 1) до плоскости Охz.
Вычислите угол между векторами
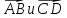 , если А(5;-8;-1), В(6;-8;-2), С(7;-5;-11), D(7;-7;-9).
, если А(5;-8;-1), В(6;-8;-2), С(7;-5;-11), D(7;-7;-9).В тетраэдре ABCD точка M – середина ребра AC. Выразите
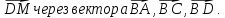
Точка D(-2;1;4), точка В симметрична точке D относительно оси Оy, точка С симметрична точке В относительно начала координат. Найдите расстояние между точками D и С.
Контрольная работа «Вектора в пространстве» 3 вариант
Часть 1
ABCDA1B1C1D1 –прямоугольный параллелепипед. Назовите вектор, равный сумме векторов
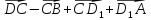 ;
;Изобразите систему координат в пространстве и A(-3; -2; 1).
Найдите длину вектора
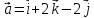 .
.Найдите координаты
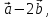 если
если 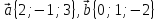 .
.Выясните, при каких значениях s и
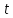 , вектора
, вектора 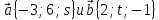 - коллинеарны.
- коллинеарны.Найдите координаты точки K, если A(1;-2;2); В(-1;4;1), а точка К-середина АВ.
Найдите скалярное произведение векторов
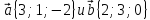 .
.
Часть 2
Найдите расстояние от точки P(5; 2; -1) до оси аппликат.
Вычислите угол между векторами
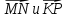 , если M(-2;3;4), N(-1;4;2), K(2;-3;6), P(1;-3;7).
, если M(-2;3;4), N(-1;4;2), K(2;-3;6), P(1;-3;7).В тетраэдре ABCD точка M – середина ребра CD. Выразите
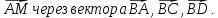
Точка A(3;1;2), точка B симметрична точке A относительно начала координат, точка C симметрична точке B относительно оси Oy. Найдите расстояние между точками A и С.
Контрольная работа «Вектора в пространстве» 4 вариант
Часть 1
ABCDA1B1C1D1 –прямоугольный параллелепипед. Назовите вектор, равный сумме векторов
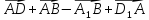 ;
;Изобразите систему координат в пространстве и A(-2; 3; -4).
Найдите длину
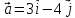 .
.Найдите координаты 3
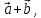 если
если 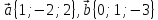 .
.Выясните, при каких значениях g и
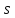 , вектора
, вектора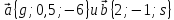 - коллинеарны.
- коллинеарны.Найдите координаты точки М, если А(0;4;-1); С(2;1;3), а точка М-середина АС.
Найти скалярное произведение векторов
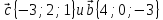 .
.
Часть 2
Найдите расстояние от точки F(3; -2; 4) до плоскости Охy.
Вычислите угол между векторами
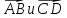 , если А(-1;-8; 5), В(-2;-8; 6), С(7; -11; -5), D(7; -9; -7).
, если А(-1;-8; 5), В(-2;-8; 6), С(7; -11; -5), D(7; -9; -7).В тетраэдре ABCD точка M – середина ребра AB. Выразите
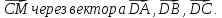
Точка D(-2;1;4), точка В симметрична точке D относительно плоскости Оxy, точка С симметрична точке В относительно начала координат. Найдите расстояние между точками D и С.



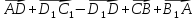 ;
;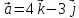 .
.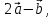 если
если 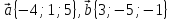 .
.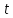 , вектора
, вектора 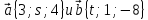 - коллинеарны.
- коллинеарны.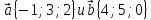 .
.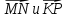 , если
, если 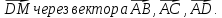
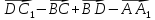 ;
;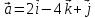 .
.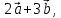 если
если 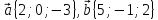 .
.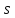 , вектора
, вектора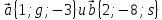 - коллинеарны.
- коллинеарны.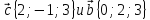 .
. 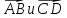 , если А(5;-8;-1), В(6;-8;-2), С(7;-5;-11),
, если А(5;-8;-1), В(6;-8;-2), С(7;-5;-11), 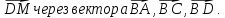
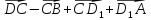 ;
;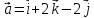 .
.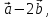 если
если 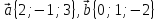 .
.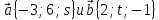 - коллинеарны.
- коллинеарны.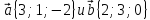 .
.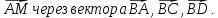
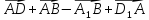 ;
;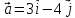 .
.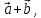 если
если 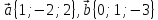 .
.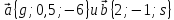 - коллинеарны.
- коллинеарны.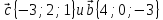 .
.