
Л.С. Атанасян. Геометрия 10-11

Аннотация.
На клетчатой бумаге с клетками размером 1 см 1 см изображены различные фигуры. Необходимо найти площадь. Ответ записать в квадратных сантиметрах.
Для того, чтобы быстро решать такие задания, надо знать формулы для вычисления площадей треугольника, прямоугольника, трапеции, параллелограмма, квадрата.
Часто при решении таких задач используются свойства площадей. Фигуру надо разбить на части, площади которых можно найти по знакомым формулам. Или наоборот, фигуру надо достроить. Получится большая фигура, площадь которой мы сможем найти.
катет
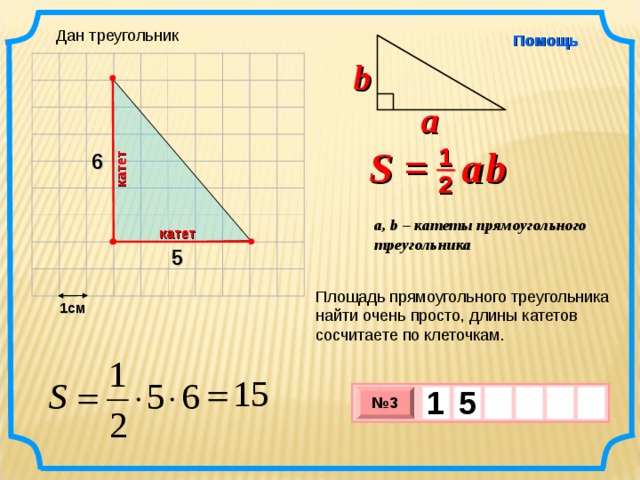
Дан треугольник
Помощь
b
a
S = a b
1
6
2
a, b – катеты прямоугольного треугольника
катет
5
Площадь прямоугольного треугольника найти очень просто, длины катетов сосчитаете по клеточкам.
1см
1
5
№ 3
х
3
х
1
0
высота
Помощь
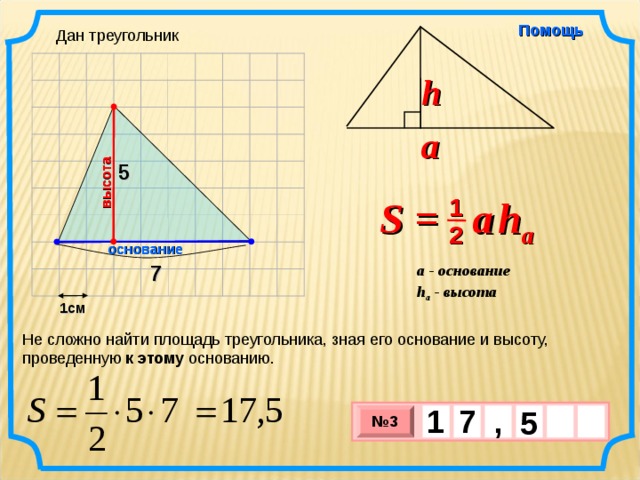
Дан треугольник
h
a
5
S = a h a
1
2
основание
7
a - основание
h a - высота
1см
Не сложно найти площадь треугольника, зная его основание и высоту, проведенную к этому основанию.
1
,
7
5
№ 3
х
3
х
1
0
основание
Помощь
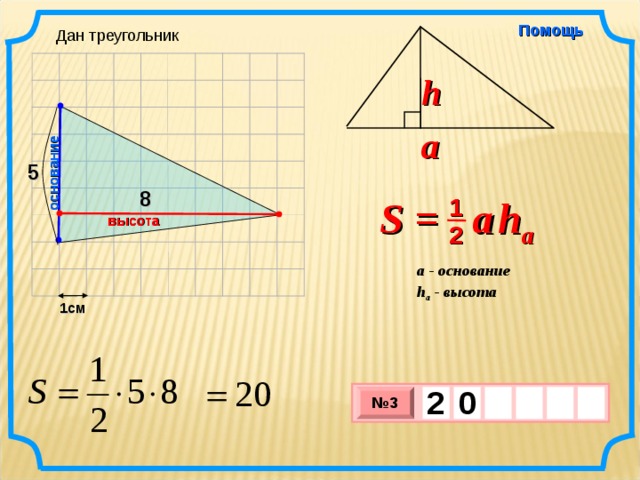
Дан треугольник
h
a
5
8
S = a h a
1
высота
2
a - основание
h a - высота
1см
2
0
№ 3
х
3
х
1
0
высота
Помощь
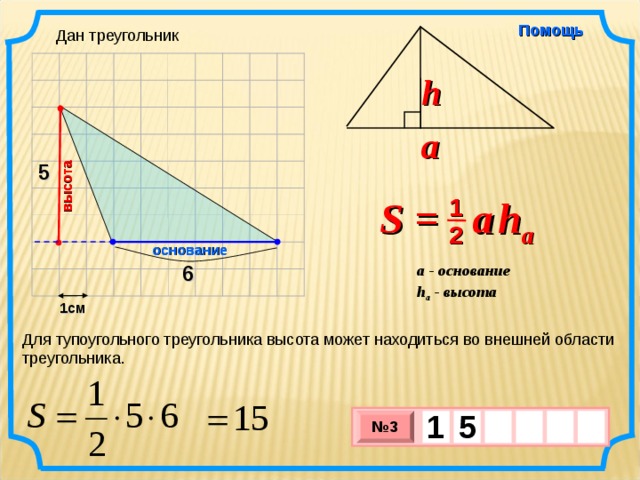
Дан треугольник
h
a
5
S = a h a
1
2
основание
6
a - основание
h a - высота
1см
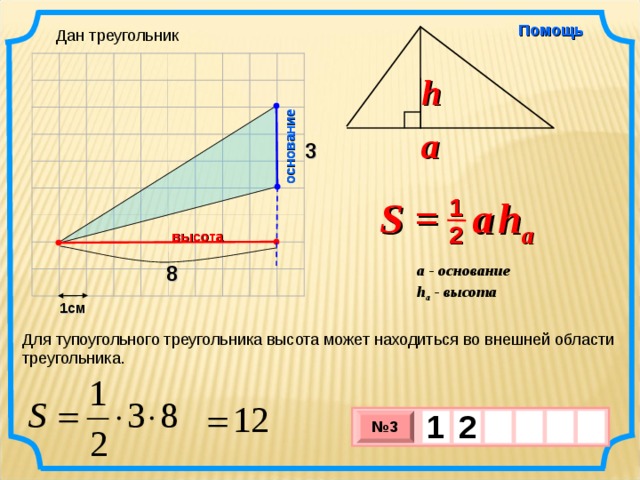
Для тупоугольного треугольника высота может находиться во внешней области треугольника.
1
5
№ 3
х
3
х
1
0
основание
Помощь
Дан треугольник
h
a
3
S = a h a
1
2
высота
8
a - основание
h a - высота
1см
Для тупоугольного треугольника высота может находиться во внешней области треугольника.
1
2
№ 3
х
3
х
1
0
Помощь
Я надеюсь, что ты помнишь:
Помощь
Дан треугольник
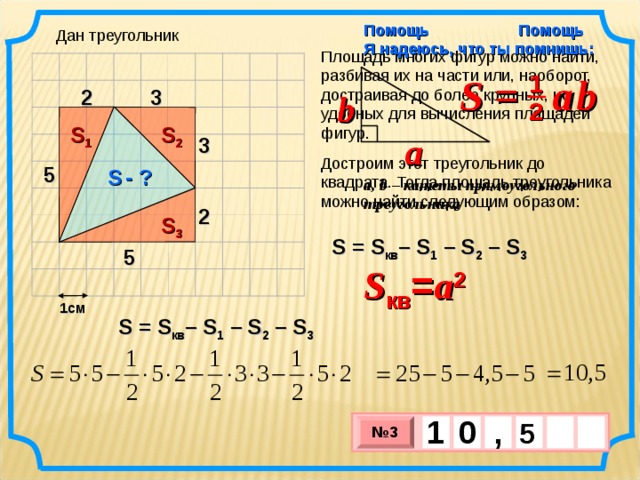
Площадь многих фигур можно найти, разбивая их на части или, наоборот, достраивая до более крупных, но удобных для вычисления площадей фигур.
S = a b
1
3
2
b
2
S 1
S 2
a
3
Достроим этот треугольник до квадрата. Тогда площадь треугольника можно найти следующим образом:
5
S - ?
a, b – катеты прямоугольного треугольника
2
S 3
S = S кв – S 1 – S 2 – S 3
5
S кв = a 2
1см
S = S кв – S 1 – S 2 – S 3
1
,
0
5
№ 3
х
3
х
1
0
основание
высота
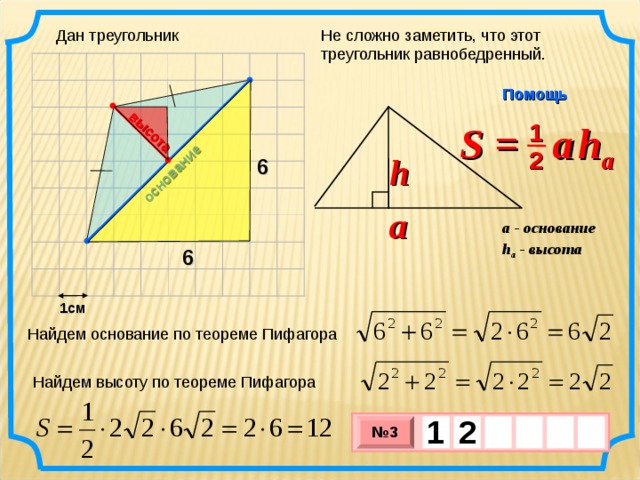
Не сложно заметить, что этот треугольник равнобедренный.
Дан треугольник
Помощь
S = a h a
1
2
h
6
a
a - основание
h a - высота
6
1см
Найдем основание по теореме Пифагора
Найдем высоту по теореме Пифагора
1
2
№ 3
х
3
х
1
0
Дан треугольник
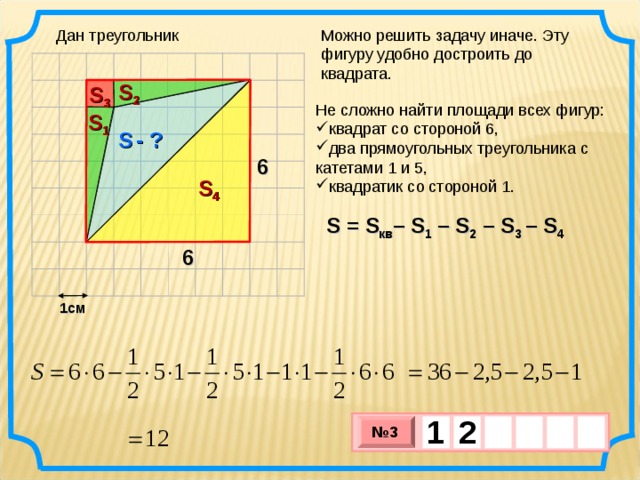
Можно решить задачу иначе. Эту фигуру удобно достроить до квадрата.
S 2
S 3
Не сложно найти площади всех фигур:
- квадрат со стороной 6,
- два прямоугольных треугольника с катетами 1 и 5,
- квадратик со стороной 1.
S 1
S - ?
6
S 4
S = S кв – S 1 – S 2 – S 3 – S 4
6
1см
1
2
№ 3
х
3
х
1
0
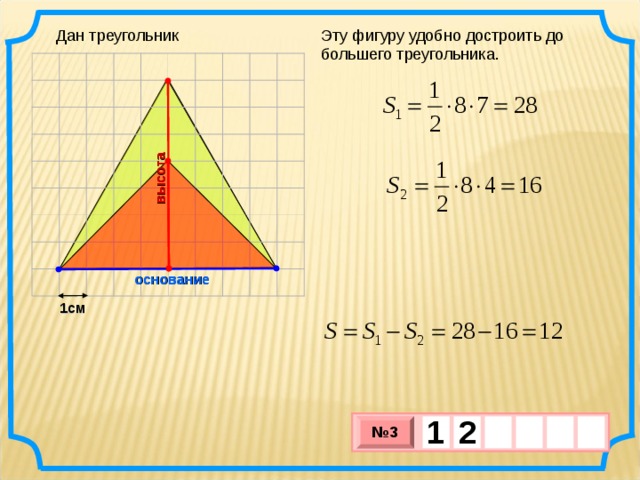
высота
Эту фигуру удобно достроить до большего треугольника.
Дан треугольник
основание
1см
1
2
№ 3
х
3
х
1
0
высота
a
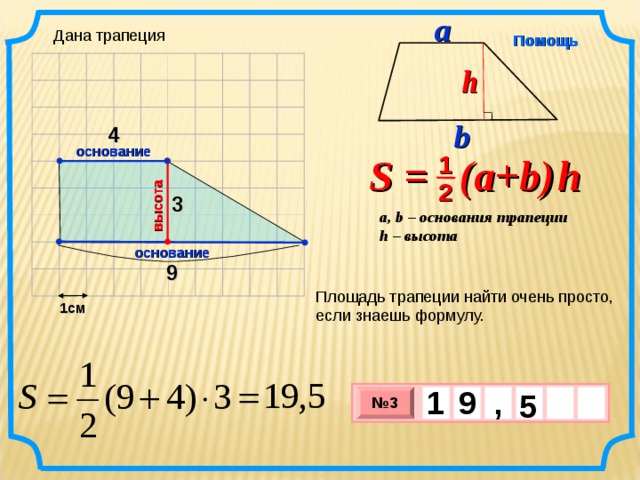
Дана трапеция
Помощь
h
b
4
основание
S = (a+b ) h
1
2
3
a, b – основания трапеции
h – высота
основание
9
Площадь трапеции найти очень просто, если знаешь формулу.
1см
1
,
9
5
№ 3
х
3
х
1
0
высота
a
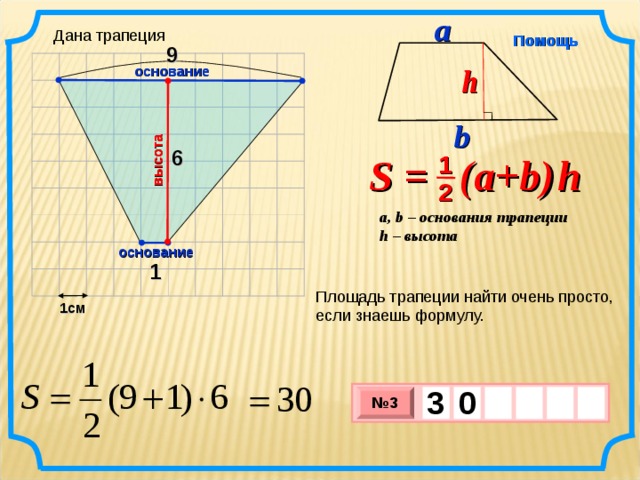
Дана трапеция
Помощь
9
h
основание
b
6
S = (a+b ) h
1
2
a, b – основания трапеции
h – высота
основание
1
Площадь трапеции найти очень просто, если знаешь формулу.
1см
3
0
№ 3
х
3
х
1
0
основание
основание
a
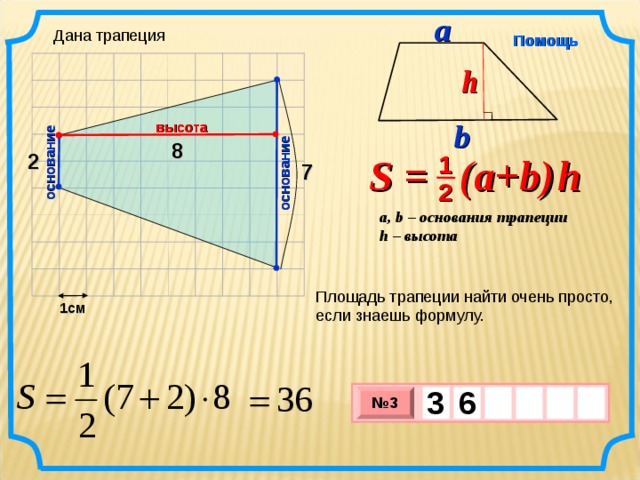
Дана трапеция
Помощь
h
b
высота
8
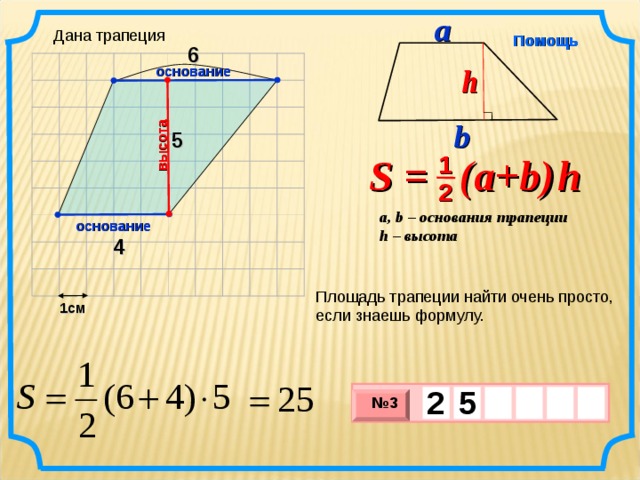
S = (a+b ) h
2
1
7
2
a, b – основания трапеции
h – высота
Площадь трапеции найти очень просто, если знаешь формулу.
1см
3
6
№ 3
х
3
х
1
0
высота
a
Дана трапеция
Помощь
6
h
основание
b
5
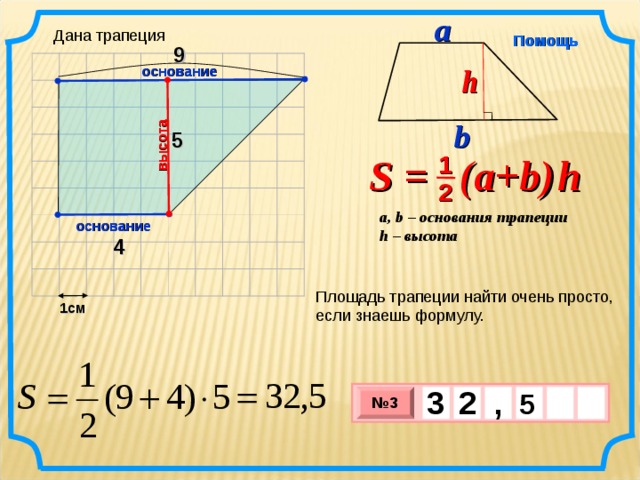
S = (a+b ) h
1
2
a, b – основания трапеции
h – высота
основание
4
Площадь трапеции найти очень просто, если знаешь формулу.
1см
2
5
№ 3
х
3
х
1
0
высота
a
Дана трапеция
Помощь
9
h
основание
b
5
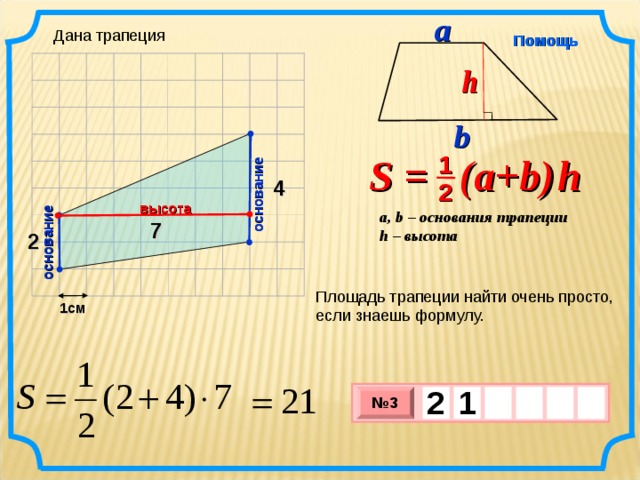
S = (a+b ) h
1
2
a, b – основания трапеции
h – высота
основание
4
Площадь трапеции найти очень просто, если знаешь формулу.
1см
3
,
2
5
№ 3
х
3
х
1
0
основание
основание
a
Дана трапеция
Помощь
h
b
S = (a+b ) h
1
4
2
высота
a, b – основания трапеции
h – высота
7
2
Площадь трапеции найти очень просто, если знаешь формулу.
1см
2
1
№ 3
х
3
х
1
0

a
Выполним дополнительные построения так, чтобы получить фигуры, площади которых мы сможем вычислить.
Помощь
h
b
S = (a+b ) h
1
3
S 1
2
7
a, b – основания трапеции
h – высота
S 2
1
S 3
1
Если на экзамене ты разволновался и забыл формулу для вычисления площади трапеции…
Ты получишь тот же ответ, но ты должен понимать, что потратишь больше времени!
1см
А мне этот способ не понравился!
2
1
№ 3
х
3
х
1
0
высота
высота
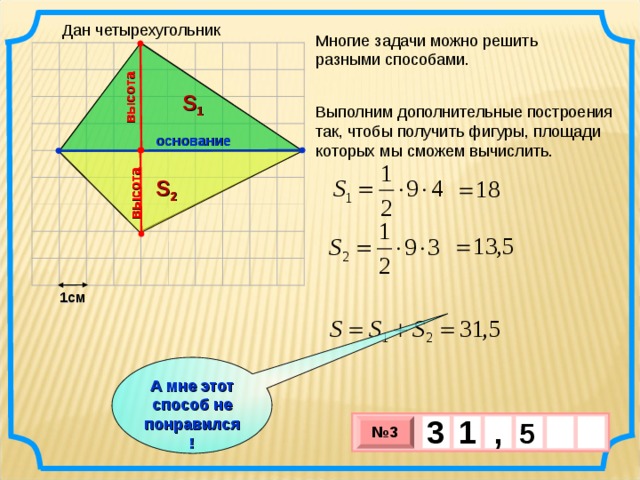
Дан четырехугольник
Многие задачи можно решить разными способами.
S 1
Выполним дополнительные построения так, чтобы получить фигуры, площади которых мы сможем вычислить.
основание
S 2
1см
А мне этот способ не понравился!
3
,
1
5
№ 3
х
3
х
1
0
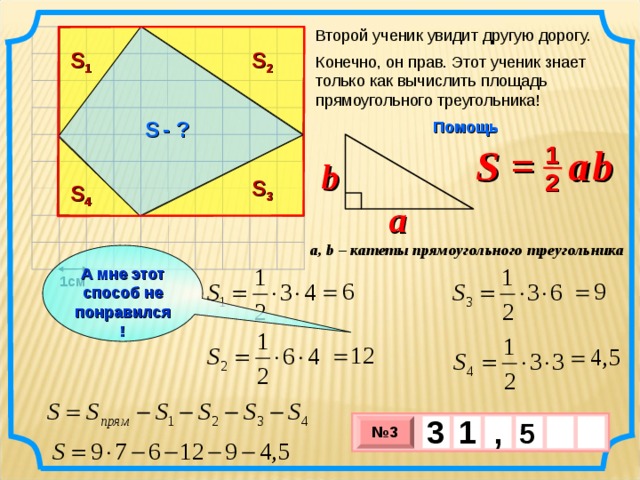
Второй ученик увидит другую дорогу.
S 1
S 2
Конечно, он прав. Этот ученик знает только как вычислить площадь прямоугольного треугольника!
S - ?
Помощь
S = a b
1
b
2
S 3
S 4
a
a, b – катеты прямоугольного треугольника
А мне этот способ не понравился!
1см
3
,
1
5
№ 3
х
3
х
1
0
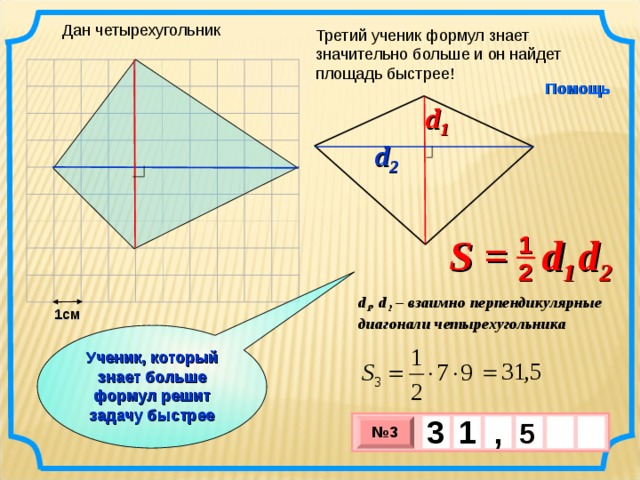
Дан четырехугольник
Третий ученик формул знает значительно больше и он найдет площадь быстрее!
Помощь
d 1
d 2
S = d 1 d 2
1
2
d 1 , d 2 – взаимно перпендикулярные диагонали четырехугольника
1см
Ученик, который знает больше формул решит задачу быстрее
3
,
1
5
№ 3
х
3
х
1
0
высота
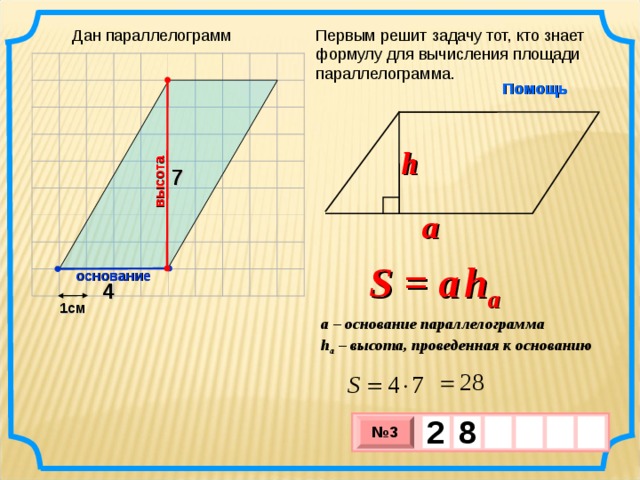
Дан параллелограмм
Первым решит задачу тот, кто знает формулу для вычисления площади параллелограмма.
Помощь
h
7
a
S = a h a
основание
4
1см
a – основание параллелограмма
h a – высота, проведенная к основанию
2
8
№ 3
х
3
х
1
0
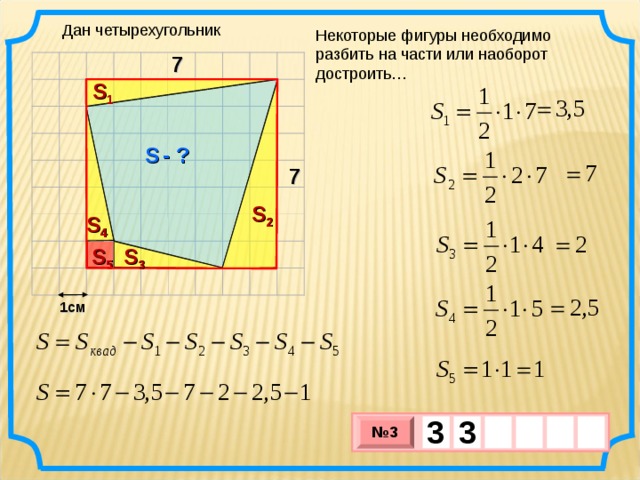
Дан четырехугольник
Некоторые фигуры необходимо разбить на части или наоборот достроить…
7
S 1
S - ?
7
S 2
S 4
S 3
S 5
1см
3
3
№ 3
х
3
х
1
0
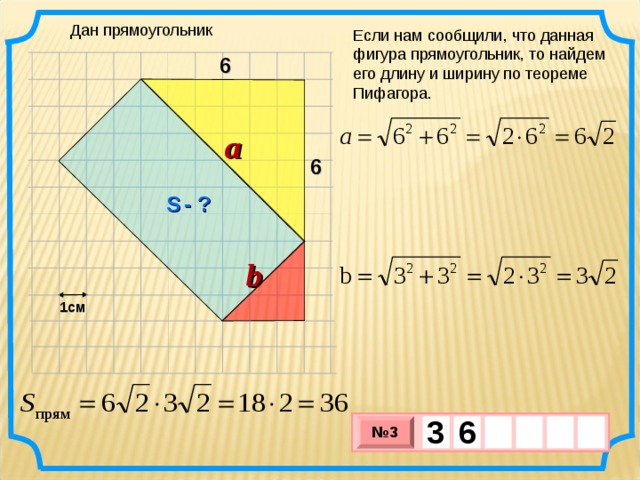
Дан прямоугольник
Если нам сообщили, что данная фигура прямоугольник, то найдем его длину и ширину по теореме Пифагора.
6
a
6
S - ?
b
1см
3
6
№ 3
х
3
х
1
0
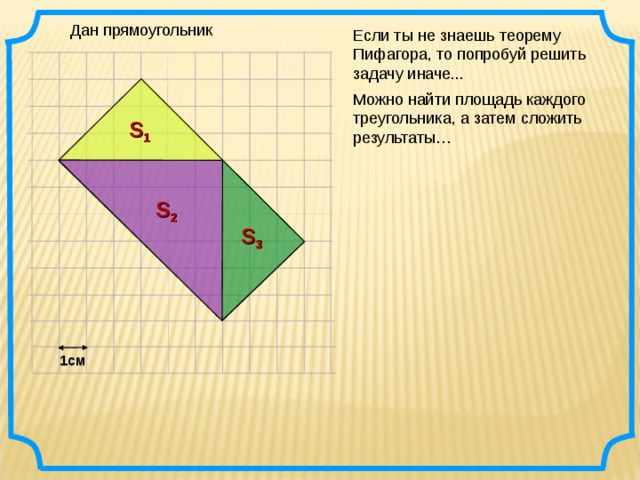
Дан прямоугольник
Если ты не знаешь теорему Пифагора, то попробуй решить задачу иначе...
Можно найти площадь каждого треугольника, а затем сложить результаты…
S 1
S 2
S 3
1см
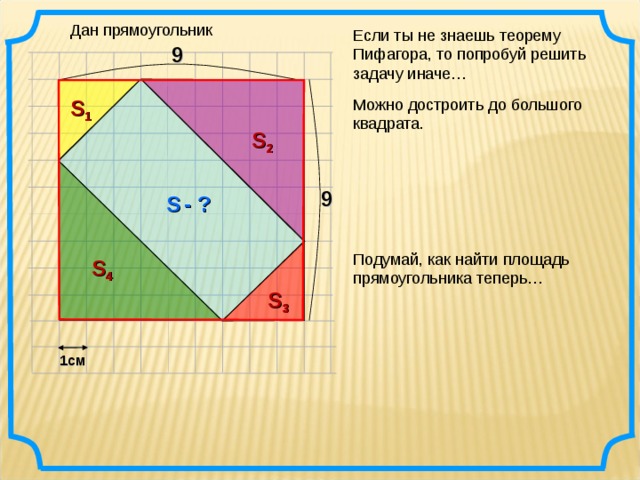
Дан прямоугольник
Если ты не знаешь теорему Пифагора, то попробуй решить задачу иначе…
9
S 1
Можно достроить до большого квадрата.
S 2
9
S - ?
Подумай, как найти площадь прямоугольника теперь…
S 4
S 3
1см







