Тема « Решение системы линейных неравенств с одной переменной»
Тип урока: изучение нового материала и первичное закрепление.
Дидактическая цель: создать условия для осознания и осмысления блока новой учебной информации.
Цели:1) Образовательная: создать условия для освоения каждым учеником стандарта образования; ввести понятия: решение систем неравенств, равносильные системы неравенств и их свойства; научить применять эти понятия при решении простейших систем неравенств с одной переменной.
2) Развивающая: способствовать развитию элементов творческой, самостоятельной деятельности обучающихся; развивать речь, умение мыслить, анализировать, обобщать, высказывать свои мысли четко, лаконично.
3) Воспитательная: воспитание уважительного отношения друг к другу и ответственного отношения к учебному труду.
Задачи:
повторить теорию по теме числовые неравенства и числовые промежутки;
привести пример задачи, которая решается системой неравенств;
рассмотреть примеры решения систем неравенств;
выполнить самостоятельную работу.
Оборудование:
мультимедиа; фолипчарты;
карточки задания в двух вариантах; (приложение 1,3)
раздаточные таблицы – подсказки для каждого обучающегося;
(приложение 2,4)
Формы организации учебной деятельности: -фронтальная – коллективная- индивидуальная.
Методы: объяснительно – иллюстративный.
ПЛАН УРОКА
| Блоки | Этапы урока | Время |
| 1 |
| 8 мин. |
| 2 | Основная часть:
| 25 мин. |
| 3 | Домашнее задание и рекомендации по его выполнению | 2 мин. |
| 4 | Подведение итогов урока:
| 10 мин. |
Ход урока.
Орг. момент.
Сегодня мы будем работать в группах.
Правила работы в группах: 1.Участвуют все;2.Выслушиваются мнения всех;
3.На каждом этапе урока выбираем спикера- человека, который отвечает;4. Готовность группы -3 хлопка
2.Неравенство может быть хорошим помощником. Только надо знать, когда к нему необходимо обратиться за помощью. На языке неравенств нередко формулируется постановка задач во многих приложениях математики. Например, многие экономические задачи сводятся к исследованию систем линейных неравенств. Поэтому важно уметь решать системы неравенств. А что же значит – «решить систему неравенств»? Это мы и разберем сегодня на уроке.
Для повторения теории темы «Неравенства и их свойства», проведем тестирование с последующей проверкой беседой по теории данной темы.
Индивидуальное выполнение теста, самооценка, оценка в парах.
Каждое задание теста предполагает ответ «Да» - фигура
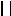 , «Нет» - фигура.
, «Нет» - фигура. 
Верно ли утверждение: если х2 и у14, то х+у 16?
Верно ли утверждение: если х2 и у14, то х·у
Является ли число 0 решением неравенства 3х-1
Является ли неравенство 3х+ 122х – 2 строгим?
Существует ли целое число, принадлежащее промежутку
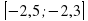 ?
?Верно ли, что при умножении или делении обеих частей неравенства на отрицательное число, знак неравенства не меняется?
Ответ проверяется с помощью интерактивной доски
(ответ:  ).
).
Записать в тетради « дата, кл. работа»
Работа в группе. Обсудить и найти правильный ответ, готовность группы- три хлопка.
Множество чисел, удовлетворяющих неравенству -4 5 изображено на рисунке… Ответ:4).
Числовой промежуток (
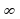 ; 9] изображен на рисунке…
; 9] изображен на рисунке…
Ответ:3). (слайд 5)
Решить, обсудить решение на месте в группе, готовность -3 хлопка.
Установить соответствие между неравенством и числовым промежутком .
«Математика учит преодолевать трудности и исправлять собственные ошибки». Найдите ошибку в решении неравенства, объясните почему допущена ошибка.
Вызов.
Задача: Автомобиль по горной дороге за 7 часов проезжает больше 210 км, а по шоссе за 5 часов – не более 400 км. В каких пределах может изменяться его скорость? (слайд 9). Задание группам: составить краткую запись, использую схему. Составление математической модели
Постановка проблем: требуется найти такие значения х, при которых верны оба неравенства, т.е. найти общее решение этих неравенств. В таких случаях говорят, что надо решить систему неравенств, и используют следующую запись

7х 210,
5х 400.
400.
Новая тема. Записать в тетрадь название темы «Решение систем линейных неравенств с одной переменной» .
- Как вы думаете, что называется решением системы неравенств?
(Решением системы неравенств с одной переменной называется значение переменной, при котором верно каждое из неравенств системы)
- Что значит « Решить систему неравенств»?
(Решить систему неравенств – значит найти все её решения или доказать, что решений нет)
Решить самостоятельно систему в задаче на движение автомобиля и ответить на вопрос задачи.
Составить алгоритм решения систем неравенств. Каждая группа получает задание ранжировать алгоритм решения систем неравенств.
3. Решение примеров .
Решить, обсудить в группе, самооценка, оценка учащихся, занести в оценочный лист.
4. Закрепление темы. Работа с учебником (стр.379 № 1575(1),1576(1)
5. Домашнее задание: п.8.6 читать, рассмотреть примеры 1-4,
решить № 1576(2,4), 1575(2,4).
7. Подведение итогов урока (выставляются оценки)
Рефлексия: - Какую тему рассмотрели сегодня на уроке?
- В чем испытали затруднения?
- Над чем необходимо еще поработать?
Проанализируйте свою работу на уроке и поставьте себе оценку «*» - все понимаю; «о»- понимаю, но есть вопросы; «?» -затрудняюсь решать системы неравенств.
Карточка №1
Решите неравенство и найдите наименьшее целое число, удовлетворяющее неравенству 8·(6 – у)  24,2 – 7у
24,2 – 7у
Карточка №2 Решите неравенство и найдите наибольшее целое число, удовлетворяющее неравенству  5
5
Приложение 2
Алгоритм решения систем неравенств с одной переменной
1. Решить каждое неравенство системы.
2. Изобразить графически решения каждого неравенства на координатной прямой.
3. Найти пересечение решений неравенств на координатной прямой.
4. Записать ответ в виде числового промежутка.
Приложение 3
Самостоятельная работа
Вариант1
Решите систему неравенств:

а) х + 3 0,
2x  5;
5;

б) х -4 5 – 2x,
3 – 2x x;

в) 2х - 5 4 – 3( х – 2),
4 – 3( х – 2),
- 2х  4.
4.
Вариант2
Решите систему неравенств:

а) х - 1
2x  1;
1;

б) х -3 3x - 5,
2x + 7 3;

в) 3 – 4 (x -1) 3 х + 8,
3 х + 8,
3х - 5 4.
4.



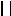 , «Нет» - фигура.
, «Нет» - фигура. 
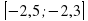 ?
?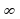 ; 9] изображен на рисунке…
; 9] изображен на рисунке… 



