| Урок 72. | Признак возрастания и убывания функции | 10 класс | 21.02.2017г |
Цели урока:
общеобразовательные:
Совершенствование умений нахождения производных; возрастания, убывания функции при решении заданий;
Закрепить и углубить знания учащихся о производной;
Показать широкий спектр применения производной;
Формирование умений по применению знаний и способов действий изменённых в новых учебных ситуациях;
развивающие:
развитие подсознательной активности учащихся;
развитие навыков самостоятельной поисковой работы.
воспитательные:
формирование у учащихся понятий о научной организации труда;
формирование умений по рецензированию собственных ответов и ответов одноклассников.
Организационный момент.
Положительный настрой: Здравствуйте, дети! Я рада вас видеть и очень хочу начать работу с вами! Хорошего вам настроения и успехов!
Продолжите предложение. Пусть этот урок принесет…
Заполнение листа ответов.
Актуализация опорных знаний учащихся.
Найдите область определения функции: а) у=√2x-4, b) f(x)=3x2-7x+4,
в) y=
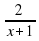 ), г)y=
), г)y= 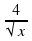
Решите неравенства: 1) 3x+20, 2) x2-3x+2
Теория. Вопрос – ответ. Ученики задают вопросы по теме друг другу, при затруднении можно пользоваться учебником.
а) Дать понятие приращения аргумента.
Ответ: Разность значений аргумента в точке х.
б) Сформулируйте определение возрастания и убывания функции.
в) В чём состоит механический смысл производной?
Ответ: производная функции y = f(x) в точке x0 - это скорость изменения функции f (х) в точке x0 x'(t). = (t)
г) В чём состоит геометрический смысл производной?
Ответ: значение производной f '(x) при данном значении аргумента x равно тангенсу угла образованного с положительным направлением оси Ox касательной к графику функции f(x) в точке M(x, f(x)). k = tg = f '(x0).
Проверка домашнего задания по образцу
Учащиеся проверяют правильность решений и выставляют оценку в свой оценочный лист.
Решение заданий.
( работа в парах, с последующей взаимопроверкой).
Установить соответствие между функциями и соответствующими им производными. (Учащиеся записывают в тетрадь ответ в виде пары, где на первом месте стоит цифра-номер функции, а на втором – буква соответствующая этой функции производная)
| f(x) | f´(x) |
| 1. y= хn | A. y´= C |
| 2. y= cos x | B. y´= cos x |
| 3. y= sin x | C. y´= -(1/x2) |
| 4. y= 1/x | D. y´= nxn-1 |
| 5. y= Cx | E. y´= -sin x |
Ответ: 1 – D, 2 – Е, 3 – В, 4 – С, 5 – А.
Учащиеся проверяют правильность решений и выставляют оценку в свой оценочный лист.
Самостоятельная работа. С последующей взаимопроверкой и решением у доски.
Карточка №1.
Найдите силу, действующую на тело массой 7 кг, движущееся по закону s(t) = 4t2 – 5t + 3 в момент времени t = 2с.
Найдем промежутки возрастания и убывания функции f(x)=2х3-3х2-12х-1
Карточка №2.
Точка движется прямолинейно по закону х(t) = 3t2 + t + 2. Найдите ускорение в момент времени t =3.
Найдем промежутки возрастания и убывания функции f(x)= 3х3-3х2+х-6
Карточка №3.
1. Точка движется прямолинейно по закону х(t) =5t3+3. Найдите скорость движения при t=4 (время измеряется в секундах, координата в метрах).
Найдем промежутки возрастания и убывания функции
f(x)= 3х3-6х2+4х-7
Карточка №4.
Точка движется прямолинейно по закону х(t) =4t2-15t4. Найдите скорость движения при t=2 (время измеряется в секундах, координата в метрах).
Найдем промежутки возрастания и убывания функции
f(x)= х3-7х2+16х-7
Итог урока и оценивание учащихся. Подсчет баллов, выставление оценок.
Домашнее задание
РЕФЛЕКСИЯ Ответьте на вопросы:
Что мне понравилось на уроке?
Какие проблемы испытывала на уроке?
Достигли ли вы поставленной цели?
| Ф.И. ученика
| ||
| Задание | Баллы | В чем трудность? |
| Устная работа
|
|
|
| Домашнее задание |
|
|
| Установить соответствие |
|
|
| Самостоятельная работа |
|
|
| Общее количество баллов |
|
|
| Оценка
|
|
|
| Ф.И. ученика
| ||
| Задание | Баллы | В чем трудность? |
| Устная работа
|
|
|
| Домашнее задание |
|
|
| Установить соответствие |
|
|
| Самостоятельная работа |
|
|
| Общее количество баллов |
|
|
| Оценка
|
|
|
| Ф.И. ученика
| ||
| Задание | Баллы | В чем трудность? |
| Устная работа
|
|
|
| Домашнее задание |
|
|
| Установить соответствие |
|
|
| Самостоятельная работа |
|
|
| Общее количество баллов |
|
|
| Оценка
|
|
|
Производная
Установить соответствие между функциями и соответствующими им производными. записать в тетрадь ответ в виде пары, где на первом месте стоит цифра-номер функции, а на втором – буква соответствующая этой функции производная
| f(x) | f´(x) |
| 1. y= хn | A. y´= C |
| 2. y= cos x | B. y´= - |
| 3. y= sin x | C. y´= - |
| 4. y= | D. y´= nxn-1 |
| 5. y= Cx | E. y´= -sin x |
| 6. y=ctgx | F. y´= |
| 7. y= tgx | G. |
Производная
Установить соответствие между функциями и соответствующими им производными. записать в тетрадь ответ в виде пары, где на первом месте стоит цифра-номер функции, а на втором – буква соответствующая этой функции производная
| f(x) | f´(x) |
| 1. y= хn | A. y´= C |
| 2. y= cos x | B. y´= - |
| 3. y= sin x | C. y´= - |
| 4. y= | D. y´= nxn-1 |
| 5. y= Cx | E. y´= -sin x |
| 6. y=ctgx | F. y´= |
| 7. y= tgx | G. |
Признак возрастания и убывания
функции
Самостоятельная работа.
Карточка №1.
Найдите силу, действующую на тело массой 7 кг, движущееся по закону s(t) = 3t3 – 5t² + 3 в момент времени t = 2с.
Найдем промежутки возрастания и убывания функции f(x)=2х3-3х2-12х-1
Карточка №2.
Точка движется прямолинейно по закону х(t) = 3t2 + t + 2. Найдите ускорение в момент времени t =3.
Найдем промежутки возрастания и убывания функции f(x)= 3х3-3х2+х-6
Карточка №3.
1. Точка движется прямолинейно по закону х(t) =5t3+3. Найдите скорость движения при t=4 (время измеряется в секундах, координата в метрах).
Найдем промежутки возрастания и убывания функции
f(x)= 3х3-6х2+4х-7
Карточка №4.
Точка движется прямолинейно по закону х(t) =4t2-15t4. Найдите скорость движения при t=2 (время измеряется в секундах, координата в метрах).
Найдем промежутки возрастания и убывания функции
f(x)= х3-7х2+16х-7
Признак возрастания и убывания
функции
Самостоятельная работа.
Карточка №1.
Найдите силу, действующую на тело массой 7 кг, движущееся по закону s(t) = 3t3 – 5t² + 3 в момент времени t = 2с.
Найдем промежутки возрастания и убывания функции f(x)=2х3-3х2-12х-1
Карточка №2.
Точка движется прямолинейно по закону х(t) = 3t3 + t + 2. Найдите ускорение в момент времени t =3.
Найдем промежутки возрастания и убывания функции f(x)= 3х3-3х2+х-6
Карточка №3.
Точка движется прямолинейно по закону х(t) =5t3+3. Найдите скорость движения при t=4 (время измеряется в секундах, координата в метрах).
Найдем промежутки возрастания и убывания функции
f(x)= 3х3-6х2+4х-7
Карточка №4.
Точка движется прямолинейно по закону х(t) =4t2+15t4. Найдите скорость движения при t=2 (время измеряется в секундах, координата в метрах).
Найдем промежутки возрастания и убывания функции
f(x)= х3-7х2+16х-7
Ответы.
Установить соответствие
Ответ: 1 – D, 2 – Е, 3 – G, 4 – С, 5 – А, 6- В, 7 - F
Признак возрастания и убывания
функции
Самостоятельная работа.
Карточка №1.
182 2.
Карточка №2.
162 2.
Карточка №3.
240 2.
Карточка №4.
496 2.



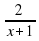 ), г)
), г)