Урок математики в 6 классе. «Системные линейные уравнения».
Урок сопровождается мультимедийной презентацией. В ходе урока прослеживаются межпредметные связи, так как урок является отчасти интегрированным. Во второй половине урока ученики отвечают на вопросы викторины посвященной Великой победе.
На уроке используются различные формы работы: фронтальная, групповая, работа в парах. Подобраны разнообразные задания, которые подготавливают учащихся к контрольной работе по данной теме.
Тема: Решение систем уравнений с двумя переменными различными способами.
Цель: Обучающие:
Систематизировать знания по теме;
Продолжить развитие навыков аналитического мышления, умения применять знания в нестандартных ситуациях;
Продолжить развитие познавательного интереса к различным предметам
Развивающие:
Развить умение мобилизовать и применять все имеющиеся знания, умения и навыки при самостоятельном решении задач;
Развивать логическое мышление, речь, волю, эмоции;
Развитие конструктивного, алгоритмического мышления благодаря особенностям общения ;
Развитие творческого мышления за счет уменьшения доли репродуктивной деятельности;
Формирование информационной культуры, умения обрабатывать информациии.
Воспитательные:
Воспитывать чувство ответственности, умение работать в коллективе;
Воспитать умение использовать свой интеллект, волю, эмоции для достижения общей цели.
Оборудование:
Проектор, экран, компьютеры, плакат для защиты способов решения систем уравнений.
Ход урока
I. Организационный момент
Здравствуйте, ребята! Сегодня на уроке предлагаю действовать, чтобы как можно больше показать свои знания. Работать будем в группах. Деятельность групп будет оцениваться спикерами по картам деятельности. Мы должны работать так, чтобы восхищаться своими знаниями, а для этого вытащим из тайников памяти кое-что ценное по темам предыдущих уроков. Используем три метода решения - графический, метод подстановки и метод алгебраического сложения, и выделим преимущества и недостатки каждого способа.
Как вы думаете, какова цель нашего урока? (Закрепить знания и умения решения систем уравнений различными способами, обобщить изученный материал по данной теме, применять изученный материал в нестандартных ситуациях). И не зря эпиграфом к нашему уроку у каждой группы следующие слова:
1 группа :«Ум заключается не только в знании, но и в умении прилагать знания на деле». Аристотель.
Обратите внимание на слова Дж. Бернарда Шоу которые использует 2 группа «Деятельность – единственный путь к знанию».
3 группа: «Математику нельзя изучать, наблюдая как это делает сосед» слова А.Нивен.
Как вы понимаете смысл этих слов? (Знания приносят пользу человеку только в том случае, когда они применяются на практике.)
II. Устный работа.
- Атлет придя на тренировку не хватает штангу без разминки, каратисты начинают с медитации, а мы «Проверим себя», где вспомним необходимые факты.
Что называют системой уравнений? (Системой уравнений называется несколько уравнений, для которых требуется найти значения неизвестных, удовлетворяющих одновременно всем этим уравнениям.
А в каких областях наук вы встречались с какими-либо системами? (биология например (система кровообращения ), физика (система СИ), природоведение (солнечная система, химия (система Менделеева).
Что является решением системы линейного уравнения с двумя переменными? (Решением системы уравнений с двумя переменными является пара значений приводящих данные уравнения к верным равенствам)
Сколько решений может иметь система линейных уравнений с двумя переменными? (Система может иметь одно решение, бесконечное множество решений или ни одного решения)
Какими способами решаются системы уравнений? (Существует три способа решения систем уравнений – способ подставки, способ сложения и графический способ)
Давайте еще раз напомним себе, на что нужно обратить внимание, при выборе метода решения системы уравнений?
Теперь главный вопрос – как решать систему?
Используем три метода решения - графический, метод подстановки и метод алгебраического сложения.
III. Закрепление материала с помощью теста.
На столах лежат карточки для работы с тестом, где вы отметите ответы. Спикерам необходимо распределить 1 тест на одного ученика по его уровню знаний.
1. Является ли пара чисел (–2; –2) решением системы уравнений:
а)  б)
б) 
(нет) (да)
2. Из какого уравнения системы и какую переменную выразить «удобнее»? Ответ объясните.
а) 
(Переменную x из первого уравнения, так как x=2y-5)
б) 
(Переменную y из второго уравнения, так как y=4x-3)
3. Сколько решений имеет система уравнений:
а)  б)
б)
(одно решение) (нет решений)
4Решите систему графически(без построения)
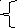
2х+у=1
8х+у=7 (1;-1)
5.Решите систему способом сложения.
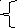
2х+у=5
3х-5у=1 (2;1)
6.Решите систему (любым способом)

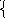
2x+4y=12
8x+5y=-7
(-4;5)
IV. Представление каждой группы решения на доске (по 3 у доски). Спикеры не забывают оценивать каждого учащегося.
V. Работа над флипчартом. Выбирают один из способов решения системы уравнений и 1 учащийся у доски , остальные записывают алгоритм решения своего способа, заполняют таблицу.
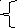 Учащиеся 1 группы, 2 группы, 3 группы решают на доске.
Учащиеся 1 группы, 2 группы, 3 группы решают на доске.
2х+у=5
-3х+2у=-4
V. Самостоятельная работа в группах
Сейчас поработайте в группах.
Задание группам:
Решите своим методом следующую систему уравнений.
Попробуйте обосновать свой вариант решения и сформулировать правило (алгоритм) решения системы.
1 группа

 2x-3y=11
2x-3y=11
4x+5y=-11
 -4x+6y=-22
-4x+6y=-22
4x+5y=-11
11y=-33
y=-3
2x-3(-3)=11
2x+9=11
2x=2
x=1
Ответ: (1;-3)
2 группа

 x+y=10
x+y=10
x-y=2
2x=12
x=6
6+y=10
y=4
Ответ: (6;4)
Отчёт групп
VI. Построение графиков в Microsoft Excel
Мы с вами вспомнили метод подстановки и метод сложения, но существует и ещё один графический метод. Давайте вспомним алгоритм решения систем уравнений графическим способом.
Обратимся к информатике и вспомним построение графиков в Excel. Ваша задача решить графически систему уравнений и построить графики в этой программе.
Какие действия нужно совершить чтобы построить диаграмму?
(Построение диаграмм
Выделить в таблице нужные для построения данные (если данные расположены в несмежных диапазонах удерживать нажатой клавишу Ctrl).
2. Щёлкнуть на кнопке Мастер Диаграмм .
В появившемся окне выбрать Тип и Вид диаграммы.
Выбрать, где расположены данные: в строках или столбцах.
Выбрать расположение Легенды (пояснения) и тип подписей данных.
Выбрать расположение диаграммы (на отдельном листе или имеющемся))
Работа в парах.
Решите графически систему

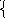 y=5-2x
y=5-2x
2y=-x
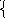 y=5-2x
y=5-2x
y=-0,5x
(Учащиеся строят графики данных функций с помощью программы Excel и получают решение данной системы уравнений)
Ответ: (3,5;-1.7)
В чём недостаток графического метода? (Недостаток графического метода решения в том, что он является неточным)
VII. Домашнее задание № 1114; № 1116. * решить систему

VIII. Итог урока
– Чем мы сегодня занимались на уроке? (Обобщали изученный материал по теме «Решение систем уравнений с двумя переменными»)
– Какими методами решали системы? ( Использовали метод подстановки, сложения и графический метод)
- Обратимся к эпиграфу урока, оправдали ли мы слова Аристотеля? (Да, действительно нужно не только знать теорию, но и уметь применять её в жизни)
Выставление оценок
IҲ. Рефлексия
Продолжите следующие фразы:
Я научился(ась):
Я продемонстрировал(а) умения:
Я запомнил(ла)…..
Мне понравилось ….
А теперь подойти к плакату на доске и отметьте человечка соответствующего вашему состоянию на уроке.

Маршрутный лист урока
Решить систему уравнений:

Не выполняя построений, найдите координаты точки пересечения графиков уравнений x-y=2 и2x+2y=14.
Составьте уравнение прямой, используя график на рисунке 29

Самостоятельная работа в группах
1 группа

2 группа

Решите графически систему

Домашнее задание № 1114; № 1116. * решить систему
Что называют системой уравнений? (Системой уравнений называется несколько уравнений, для которых требуется найти значения неизвестных, удовлетворяющих одновременно всем этим уравнениям.
А в каких областях наук вы встречались с какими-либо системами? (биология например (система кровообращения )свои примеры
Что является решением системы линейного уравнения с двумя переменными? (Решением системы уравнений с двумя переменными является пара значений приводящих данные уравнения к верным равенствам)
Сколько решений может иметь система линейных уравнений с двумя переменными? (Система может иметь одно решение, бесконечное множество решений или ни одного решения)
Какими способами решаются системы уравнений? (Существует три способа решения систем уравнений – способ подставки, способ сложения и графический способ)
Давайте еще раз напомним себе, на что нужно обратить внимание, при выборе метода решения системы уравнений?
Алгоритм решения системы уравнений с двумя переменными способом сложения.
Назовите способ решения системы линейных уравнений с двумя неизвестными, алгоритм которого записан:
Уравнять модули коэффициентов при какой-нибудь переменной
Сложить почленно уравнения системы
Составить новую систему: одно уравнение новое, другое - одно из старых
Решить новое уравнение и найти значение одной переменной
Подставить значение найденной переменной в старое уравнение и найти значение другой переменной
Записать ответ: х=…; у=… .
Алгоритм решения системы уравнений с двумя переменными графический способ.
Выразить у через х в каждом уравнении
Построить в одной системе координат график каждого уравнения
Определить координаты точки пересечения
Записать ответ: х=…; у=… , или (х; у)
Алгоритм решения системы уравнений с двумя переменными способом подстановки
Из какого-либо уравнения выразить одну переменную через другую
Подставить полученное выражение для переменной в другое уравнение и решить его
Сделать подстановку найденного значения переменной и вычислить значение второй переменной
Записать ответ: х=…; у=… .







