Харцызск 2013
Дробные числа
правильная 
неправильная
a b a b
обыкновенная дробь
Дробные числа вида называют обыкновенными дробями, или дробями. Изображаются дроби двумя натуральными числами, разделенными горизонтальной чертой, выполняющей роль знака деления.
Число, записанное под чертой, называют знаменателем дроби. Знаменатель указывает на сколько равных частей разделено одно целое. В дроби 
это число 8.
Число, записанное над чертой, называется числителем дроби. Числитель показывает сколько взято равных частей целого. В дроби это число 5.
Дробь, числитель которого меньше знаменателя, называется правильной. Например, дробь правильная, так как 5 неправильной. Например, дроби 
- неправильные, так как в первом случае 54, а во втором 5=5.
Любую неправильную дробь можно записать в виде суммы целой и дробной части.
Для этого необходимо выполнить деление с остатком числителя на знаменатель. Целая часть – это натуральное число, представляющее собой неполное частное, а дробная часть – правильная дробь, числитель которой – остаток, а знаменатель – делимое.
Алгоритм 1.
Запись результата выполнения деления с остатком:
| При делении с остатком необходимо записать: 25 : 6 = 4 (ост. 1) | |
|
25 : 6 =
|
еполное частное как целую часть
Дробное число, имеющее целую и дробную часть, называют смешанным числом.
Алгоритм 2.
Запись неправильной дроби в виде смешанной дроби| Шаг | Действие | Пример |
| 1 | Выполнить деление числителя на знаменатель | 25 : 6 |
| 2 | Выполнить алгоритм 1 |
|
Чтобы смешанное число записать в виде неправильной дроби, нужно его целую часть умножить на знаменатель и прибавить числитель, а знаменатель оставить без изменений.
Алгоритм 3.
Запись смешанной дроби в виде неправильной дроби
| Шаг | Действие | Пример |
| Чтобы смешанную дробь представить в виде неправильной дроби, нужно: |
| |
| 1 | Целую часть умножить на знаменатель дробной части и прибавить числитель | 5 7 + 6 = 41 |
| 2 | Полученное число записать в числитель дроби |
|
| 3 | Знаменатель оставить тем же | |
Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше, и меньше та дробь, у которой числитель меньше.
Чтобы сравнить две дроби с одинаковыми знаменателями, нужно сравнить их числители. Например, 
, так как 3 1.
Алгоритм 4.
Сравнение дробей с одинаковыми знаменателями
| Шаг
| Действие | Пример | |
| 1 | Сравнить знаменатели сравниваемых дробей Если знаменатели различны, то это правило для сравнения не подходит | а) 11=11 - одинаковы | б) 79, правило не подходит |
| 2 | Если числитель первой дроби больше числителя второй дроби, то первая дробь больше второй; если меньше, то и дробь меньше | 6, следовательно,
| |
.
Алгоритм 5
Правила сравнения дробей с единицей
Любая правильная дробь меньше единицы:
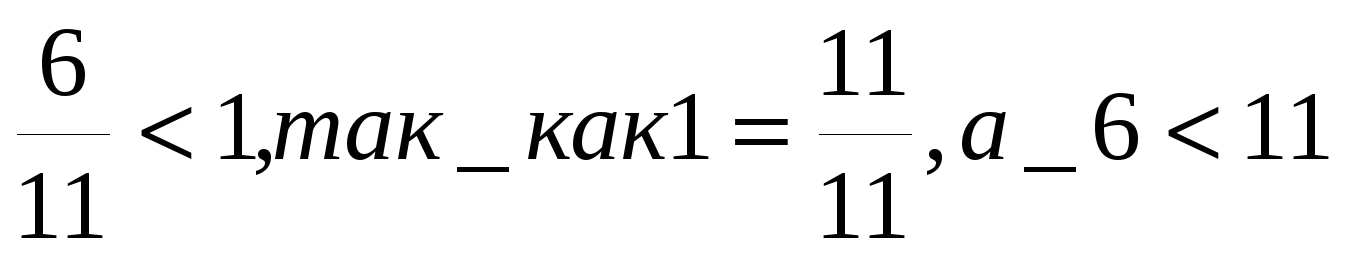
Неправильная дробь, у которой числитель равен знаменателю, равна 1:
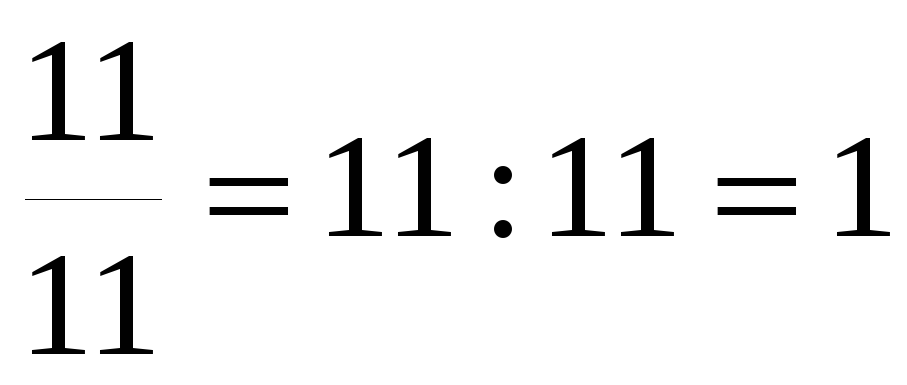
Неправильная дробь, у которой числитель и знаменатель различны, больше 1:
, так как 
а 
.
Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше.
Например, 
, так как 5
Алгоритм 6.
Сравнение дробей с одинаковыми числителями
| Шаг | Действие | Пример | |
| 1 | Проверяем, равны ли числители Если числители различны, то это правило для сравнения не подходит | а) 69, правило не подходит | б) 4=4, одинаковы |
| 2 | Сравниваем знаменатели Если знаменатель первой дроби меньше знаменателя второй дроби, то первая дробь больше второй;
если больше, то дробь меньше | 7, следовательно,
| |
.
Чтобы сложить две дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.
Алгоритм 7.
Сложение дробей с одинаковыми знаменателями
| Шаг | Действие | Пример | |
| 1 | Проверяем, равны ли знаменатели Если знаменатели различны, то это правило для сложения не подходит | а) 11=11 - одинаковы | б) 79, правило не подходит |
| 2 | Складываем числители обеих дробей и записываем в числитель результата |
| |
| 33 | Знаменатель записываем без изменений | ||
Чтобы вычесть две дроби с одинаковыми знаменателями, нужно из числителя уменьшаемого вычесть числитель вычитаемого и полученный результат записать в числитель, а знаменатель оставить тот же.
Алгоритм 8.
Вычитание дробей с одинаковыми знаменателями
| Шаг | Действие | Пример | |
| 1 | Проверяем, равны ли знаменатели Если знаменатели различны, то это правило для вычитания не подходит | а) 11=11 - одинаковы | б) 79, правило не подходит |
| 2 | Из числителя уменьшаемого вычитаем числитель вычитаемого, и результат записываем в числитель дроби |
| |
| 3 | Знаменатель записываем без изменений | ||
.
Чтобы найти сумму (разность) двух смешанных чисел, нужно отдельно найти сумму (разность) их целых и дробных частей, а затем записать их рядом, как одно дробное число.
Алгоритм 9.
Сложение смешанных дробей
| Шаг | Действие | Пример | |
| 1 | Складываются целые части |
|
|
| 2 | Складываются дробные части по алгоритму 7 Если получилась неправильная дробь, то применяем алгоритм 2 | + | + |
| 3 | Целую и дробную части записываем как одно число
| = | = |
Алгоритм 10.
Вычитание смешанных дробей
| Шаг | Действие | Пример |
| 1 | Из целой части уменьшаемого вычитается целая часть вычитаемого |
|
| 2 | Вычитаются дробные части по алгоритму 8 | + |
| 3 | Целую и дробную части записываем как одно число
| = |
Частные случаи применения алгоритма 10
1. Из числа, содержащего целую и дробную части, вычитается дробь, равная дроби уменьшаемого:
2. Из числа, содержащего целую и дробную части, вычитается дробь, причем дробь уменьшаемого больше дроби вычитаемого.
3. Из числа, содержащего целую и дробную части, вычитается число, содержащее целую и дробную части, причем дробь уменьшаемого меньше дроби вычитаемого.
| Шаг | Действие | Пример |
| 1 | У целого числа занимается единица |
|
| 2 | Эта единица вместе с дробью обращается в неправильную дробь |
|
| 3 | Применяется алгоритм 10 |
|
Чтобы найти дробь от числа, надо это число разделить на знаменатель дроби и полученный результат умножить на числитель дроби.
Алгоритм 11.
Нахождение дроби от числа
| Шаг | Действие | Пример Найти от 3200 |
| 1 | Найти сколько приходится на одну часть | Знаменатель дроби показывает, что 3200 состоит из 8 равных частей, значит, на одну часть приходится в 8 раз меньше, т.е.: 3200 : 8 =400 |
| 2 | Найти сколько приходится на количество частей, указанных в числителе | Число 3 показывает, что из 8 частей взяли 3 равные части. Следовательно, на них приходится в 3 раза больше, чем на одну часть, т.е.: 400 3 = 1200 |
Чтобы найти число по его части, надо эту часть разделить на числитель дроби и результат умножить на знаменатель дроби.
Алгоритм 12.
Нахождение числа по его дроби
| Шаг | Действие | Пример Найти длину отрезка, если составляют 12 см. |
| 1 | Найти сколько приходится на одну часть | Дробь означает, что весь отрезок разделен на 4 равные части, из них на 3 части приходится 12 см, т.е. одна часть составляет 12 : 3 = 4 (см) |
| 2 | Найти сколько приходится на количество частей, указанных в знаменателе | Так как отрезок состоит из 4 частей, то на них приходится в 4 раза больше, чем на одну часть, т.е.: 4 4 = 16 (см) |
