

Провела: Ибрагимова П. И.
– учитель математики
г. Кизилюрт – 2013г.
Тема: «Решение задач с помощью систем уравнений второй степени»
Цели урока:
Обучение составлению системы уравнений по условию задачи.
Развитие способности к содержательному обобщению и рефлексии.
Повышение интереса к решению текстовых задач.
Тип урока: изучение нового материала.
Оборудование: проектор, интерактивная доска.
Ход урока
I. Устный счет (8 мин)
Является ли решением уравнения х+2у=5 пара чисел: а) (0;1) б) (3;-1) в) (-1;3)
1. Является ли решением системы уравнений ![]() ,
,
пара чисел: а) х=1, у=6 б)х=3, у=2
2. Решите систему уравнений: ![]()
3. Определите степень уравнения:
А) х-у-1,2=0
Б)
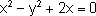
В)
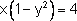
Г)
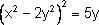
II. Изучение нового материала (10 мин)
При решении задач можно вводить две переменные и составлять систему уравнений.
Решить задачу двумя способами: «Гипотенуза прямоугольного треугольника равна 13 см. Найдите его катеты, если известно, что один из них на 7 см больше другого».
Решение:
1 способ- с помощью одной переменной.
Пусть один катет прямоугольного треугольника равен х см, а второй катет – х+7 см. Используя теорему Пифагора, составим уравнение:
х²+(х+7)²=13²
х²+х²+14х+49-169=0
2х²+14х-120=0
х²+7х-60=0
Д=49-4х1х(-60)=289
х1=-12, х2=5
корень х=-12 не удовлетворяет условию х0.
Один катет равен 5 см, второй 12 см
2 способ- с помощью введения двух переменных.
Пусть первый катет х см, второй катет у см (х0, у0)
![]() ,
,
 ,
,
![]() ,
,
2у²+14у-120=0
у²+7у-60=0
у1=5, у2=-12 (не удовл. условию)
если у=5, то х=7+5=12
один катет равен 5 см, второй катет 12 см
Ответ: 12 см, 5 см
III. Закрепление нового материала (10 мин)
Решение задач:
1. Прямоугольный газон обнесён изгородью, длина которой 30 м. Площадь газона 56 м². Найдите длины сторон газона?
Решение: пусть х м –длина газона, у-ширина газона.
![]() ,
,
![]() ,
,
у²-15у+56=0
у1=7, у2=8
х1=8, х2=7
Ответ: 7 см, 8 см
2. Двое рабочих совместно могут выполнить заданную работу за 12 дней. Если первый рабочий сделает половину работы, а затем второй – вторую половину, то вся работа будет закончена за 25 дней нужно каждому из рабочих в отдельности для выполнения работы?
Решение: пусть для выполнения всей работы первому рабочему потребуется х дней, а второму у дней, тогда за 1 день первый выполняет 1/х часть, а второй 1/у часть всей работы. Работая совместно, всю работу они выполняют за 12 дней.
Таким образом 12(1/х+1/у)=1.
Пусть теперь работа выполняется рабочими поочередно. Тогда для выполнения половины всей работы первому потребуется 1/2:1/х=х/2 дней, а второму 1/2: 1/у=у/2 дней.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
х=20 или х=30
у=50-х
Одному рабочему для выполнения всей работы требуется 20 дней, а другому 30 дней.
Ответ: 20 дней, 30 дней
Решаем по учебнику: №455, №457 (15 мин)
IV. Итог урока.
Домашнее задание: №456, №458, №460 (2 мин)










 0. Один катет равен 5 см, второй 12 см ." width="640"
0. Один катет равен 5 см, второй 12 см ." width="640"
 0, y0) x – y = 7; x = 7 + y; X 2 + y 2 = 13 2 ; (7 + y) 2 + y 2 = 169; y 1 = 5, 2y 2 + 14y – 120 = 0 y 2 +7y – 60 = 0 y 2 = -12 (не удовл.условию) Если y = 5, то x = 7 + 5 = 12 Один катет равен 5см , второй катет 12 см Ответ: 5см,12 см." width="640"
0, y0) x – y = 7; x = 7 + y; X 2 + y 2 = 13 2 ; (7 + y) 2 + y 2 = 169; y 1 = 5, 2y 2 + 14y – 120 = 0 y 2 +7y – 60 = 0 y 2 = -12 (не удовл.условию) Если y = 5, то x = 7 + 5 = 12 Один катет равен 5см , второй катет 12 см Ответ: 5см,12 см." width="640"










