Решение тригонометрических функций и неравенств

Областное государственное автономное

профессиональное общеобразовательное учреждение

«Ютановский агромеханический техникум

имени Евграфа Петровича Ковалевского»

Методическая разработка урока по математике:

Решение тригонометрических уравнений и неравенств

Выполнила:

преподаватель математики

Тарановская В.П.

2016 год

Тема урока: Решение тригонометрических уравнений и неравенств

Цель урока: повторить теоретический материал по теме: Тригонометрические функции, часто употребляемые формулы, решение неравенств, уравнений, помочь обучающимся проверить свои знания по данной теме.

Ход урока.

1. Организационный момент.

• В центре нашего внимания на уроке будет «Рабочая карта урока». Она есть у каждого из вас. Сюда вы будете вносить свою оценку за каждый этап урока. Одну из оценок поставит вам сосед по парте, одну преподаватель. А в конце урока подведете итог своей работе и выставите себе средний балл за урок, т.е. за усвоение темы «Тригонометрические функции».

Рабочая карта урока

Д/з (Решение неравенств)	Диктант. (Теория по теме)	Тест (Решение уравнений)		Оценка учителя	Итог
с/о	с/о	с/о	о/т	о/у

(с/о- самооценка, о/т- оценка товарища, о/у- оценка учителя)

1. Проверка домашней работы.

2. • На доске вы видите элементы решения неравенств из домашней работы. Запишите получившиеся неравенства.

(Обучающиеся объясняют решение неравенств с помощью единичной окружности, дают определения, проговаривают необходимые формулы)

• Вот мы и повторили решение неравенств. Те, кто выполнил домашнюю работу самостоятельно, во всем разобрался, поставьте себе «5», те, у кого появились трудности при выполнении работы или приходилось обращаться за помощью к другу – «4», если есть ошибки – «3», если работа не выполнена

- «2».

1. Диктант

• Следующий этап нашего урока – математический диктант. Думать придется много, писать мало. При ответе на любой вопрос будете писать одно из слов: «да» или «нет».

1. Является ли убывающей функция y=cos x?

2. Является ли четной функция y=sin x?

3. Верно ли, что cos² x- sin² x=1?

4. Верно ли, что arksin(-1/2)=-π/6?

5. Абсцисса точки, лежащей на единичной окружности. Называется синусом?

6. Верно ли, что косинус 6, 1 больше 0?

7. Верно ли, что область значения функции тангенс есть отрезок

от –1 до 1?

1. Отношение синуса к косинусу – это тангенс?

(обучающиеся проверяют диктант вместе с преподавателем, объясняя каждое высказывание и выставляя оценку себе в рабочую карту урока.)

1. Решение тригонометрических уравнений – тестовые задания.

   • Герберт Спенсер, английский философ, говорил: «Дороги не те

знания, которые откладываются в мозгу, как жир, дороги те, которые превращаются в умственные мышцы».

Следующее задание – решить уравнения, применяя полученные знания, разгадать кодовое слово.

Решив тестовые задания, оцените себя, поменяйтесь работами, оцените товарища. Время ограничено – 10 минут.

Тест «Тригонометрические уравнения»

cos² x + 3sin x = 3

1. – π /2 + π к, к Z

2. π /2 + 2π к, к Z

3. π + π к, к Z

4. π + 2π к, к Z

sin x + cos x + 1+ sin x cos x = 0

7. π + 2 π к, к Z; – π /2 + 2π k, k Z

8. 2πк, к Z; π /2 + 2π k, k Z

9. π + π к, к Z; π /2 + π k, k Z

10. – π + π к, к Z; – π /2+ π k, k Z

sin x – 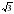cos x = 0

13. π /3 + 2π к, к Z

14. π /3 + π к, к Z

15. π /2 + 2π к, к Z

16.–π /3 + π к, к Z

tg 2x = 1

1. π /4 + π к, к Z

2. π /8 + π к/2, к Z

3. π /2 + 2π к, к Z

4. π /8 + 2π к, к Z

КОД

а	б	в	о	и	к	л	с	н	ш	р	м	е	н	т	у
15	4	13	7	19	2	8	20	18	14	1	21	9	3	16	10

5.Определение типа уравнений, способа решения.

• Среди данных уравнений выберите те, которые решаются:

а) приведением к квадратному,

б) как однородные,

в) понижением порядка,

г) с помощью формул суммы и разности,

д) с помощью универсальной подстановки.

1. 2 sin² x+cos² x =5 sin x cos x

2. sin² x+ cos² 2x+ sin² 3x=3/2

3. cos x sin 7x= cos 3x sin 5x

4. sin² x - 2 sin x - 3=0

5. sin² x - sin x=0

6. sin x+ sin 3x= sin 5x- sin x

7. sin x- sin 2x+ sin 3x- sin 4x=0

8. 2 cos² x+3 sin² x+2 cos x=0

9. cos² x+3 sin² x+2 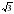sin x cos x=3

10. sin² x-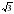/3 sin 2x= cos² x

11. sin x+ cos x=1

- Так как уравнение 3) вы не отнесли ни к одному из предложенных типов, решим его на доске.

1. Итог урока.

Общая оценка работы группы, выставление оценки за урок каждому обучающемуся, определение итоговой оценки.

Домашнее задание – решить по одному уравнению каждого типа из предложенных на доске.