"Рационал көрсеткішті дәреже" тақырыбына математикадан жұмыс дәптері

Математикадан жұмыс дәптері № 2. Оқушының аты-жөні _____________________________________________________ Күні________________________________ Тақырыбы: Рационал көрсеткішті дәрежесі бар өрнектерді түрлендіру. Сабақтың барысы: 1. Біліктілік қағидасы: Егер.... онда...... - мұғалімді зейінмен тыңдасаң тақырыпты түсінесің. - теорема, ережелерді білсең кез-келген нәрсені дәлелдей аласың. - формула жаттасаң есеп шығара аласың. 2. Білім өзектілігі. Негізгі ұғымдарды қайталау. 1) Рационал көрсеткішті дәрежеге анықтама беріңіздер______________________________ 2) Рационал көрсеткішті дәреженің қасиеттерін жазыңыздар__________________________ ___________________________________________________________________________ ___________________________________________________________________________ 3) 64 санын негізі -2; 2; 8 болатындай дәреже түрінде жазыңыздар____________________ ___________________________________________________________________________ 4) Қандай санның үшінші дәрежесі 64-ке тең болады? ______________________________ 5) 64 санын тағыда басқа тәсілмен рационал көрсеткішті дәреже түрінде көрсетуге болады ма?

3. Топпен жұмыс. 1-топ. өрнектерінің мәні болмайтынын дәлелдеңдер._________________________

__________________________________________________________________________________

2-топ. Рационал көрсеткішті дәрежені түбірмен алмастырыңыздар: 3-топ. ші дәрежелі түбірді рационал көрсеткішті дәрежемен алмастырыңыздар:

3. «Дәрежеге қолданатын амалдар» зертханасына аялдайық.

Зертхананың жиі қонақтары астраномдар. Олар өздерінің «астрономиялық сандарын» алгебралық түрлендірулер жасап, пайдалы нәтиже алады. Мысалы, Жерден тұманды Андромедаға дейінгі арақашықтығы 95000000000000000000 = 95 •10¹⁸ км санымен өрнектеледі, ол квинтиллион деп аталады. Күннің салмағы граммен 1983 •10³⁰ гр – нональон санымен өрнектеледі. Зертхана қызметкерлеріне бізде көмектесейік, өрнектерді қысқартып немесе мәнін табыңыздар.

1-топ.

2-топ.

3-топ.

4.Сандарды салыстырыңдар:

1-топ. _________________________________________________________

__________________________________________________________________________________

2-топ. ___________________________________________________________

__________________________________________________________________________________

3-топ. _____________________________________________________________

__________________________________________________________________________________

5. Шығармашылық тапсырма. Дәрежеге қандай түрлендірулер қолдана аламыз?

1) 3 санын көрсеткіші 2; 3; -1-ге тең дәреже түрінде келтіріңдер:_________________________

__________________________________________________________________________________

2) өрнектерін қандай тәсілмен көбейткіштерге жіктеуге болады?

3) Бөлшекті қысқартып, бір-бірлеріңді тексеріңдер:

4) Түрлендірудің орындалуын түсіндіріп, өрнектің мәнін табыңыздар.

Тарихқа үңілсек. Көптеген есептерді шешкенде бірдей көбейткіштерді көбейтуге тура келеді. Натурал көрсеткішті дәреже туралы ұғым Грецияда пайда болған(санның квадраты деген түсінік квадраттың ауданын есептеп шығарғанда, ал санның кубы – куб көлемін тапқанда шыққан). Ал қазіргі қолданып жүрген белгілеулерді ( сияқты) XVII ғасырда Декарт енгізген.

Дәреженің бөлшек көрсеткіштері және бөлшек көрсеткішті дәрежелерге қолданылған ең қарапайым ережелер XIV ғасырда француз математигі Н.Оремнің (1323-1382) еңбектерінде кездескен болатынды. Шюке (1445-1500 жылдар шамасында) көрсеткіші теріс және нөл болып келген дәрежелерді қарастырған еді. С.Стевин дегенді түбір деп түсінуді ұсынған. Алайда рационал көрсеткіштерді жүйелі түрде бірінші болып пайдаланған Ньютон болды.

6. Өздік жұмыс.

Қандай бөлшектерді қысқартқанда қысқаша көбейту формуласын қолдануға және ортақ көбейткішті жақша сыртына шығаруға болады?

1-топ: № 1, 2, 3.

2-топ: № 4, 5, 6.

3-топ: № 7, 8, 9.

Тапсырмаларды орындағанда төмендегі кеңестерді есте сақтаңыздар:

1. Егер есептің жазылуында рационал көрсеткішті дәрежемен 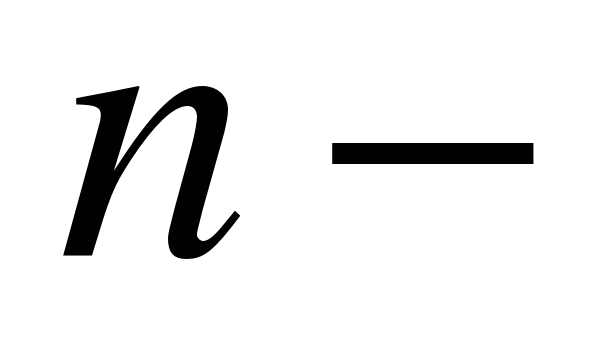ші дәрежелі түбір болса, онда 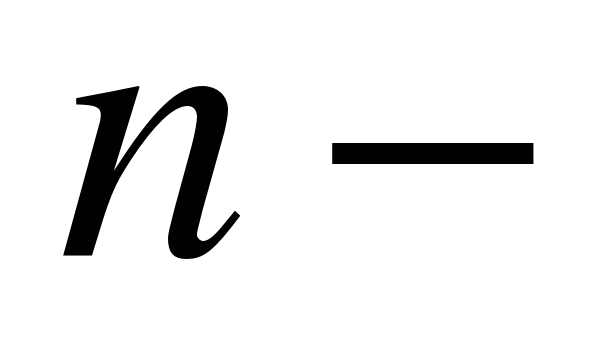ші дәрежелі түбірді рационал көрсеткішті дәреже түрінде жазыңыздар.

2. Егер жақшаларды ашу, қысқаша көбейту формулаларын қолдану, теріс көрсеткішті дәрежеден оң көрсеткішті дәрежеге көшу амалдары орындалатын болса, онда бөлшекті қысқартуға тырысыңыздар.

3. Амалдардың орындалу тәртібін анықтаңыздар.

4. Орындалу тәртібін сақтай отырып, амалдарды орындаңыздар.

7. Рефлексия. Сөйлемді аяқтаңыздар:

1. санының 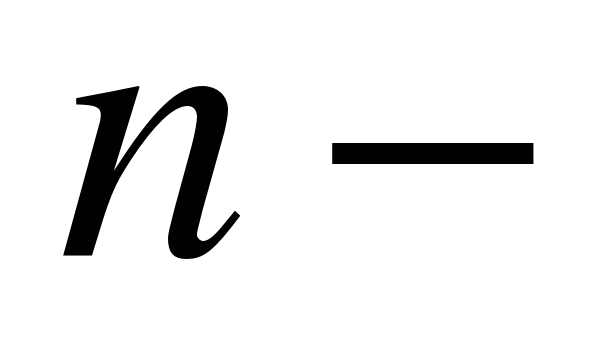ші дәрежелі түбірі деп ....

2. санының 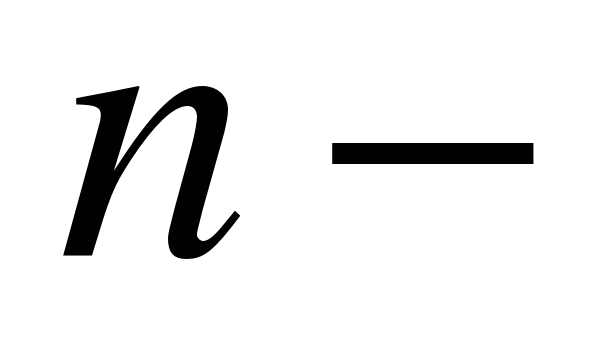ші дәрежелі түбірі деген - ....

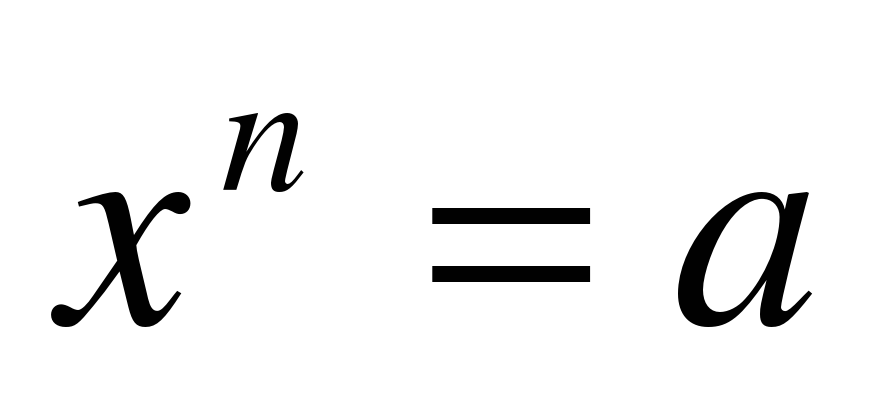3. Айнымалысы түбір белгісінің астында тұратын теңдеу ..... деп аталады.

4. 0 санының дәрежесі ... көрсеткіштер үшін анықталған.

5. Кез-келген оң саны менкез-келген рационал саны үшін 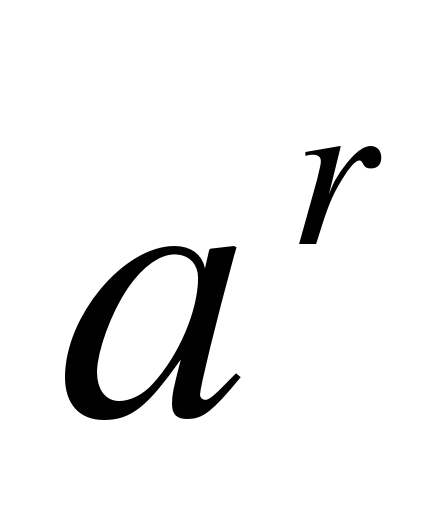..... сан болады.

8. Үйге тапсырма. № 431 (а-г), № 432 (а-г). Сандарды дәрежелеу мысалдарын құрастыру.

9. Бағалау.

Пән мұғалімі Джамбекова А.К.

3