Государственное бюджетное профессиональное образовательное учреждение
Саратовской области
«Питерский агропромышленный лицей»
Методическая разработка
открытого урока по математике
Тема урока: «Применение определенного интеграла для нахождения площади
криволинейной трапеции»


Урок подготовила и провела
преподаватель математики
высшей квалификационной категории
Сорокина Любовь Викторовна
Урок по теме «Применение определенного интеграла для нахождения площади криволинейной трапеции» изучается в конце раздела «Интегрирование», после темы «Определенный интеграл» и является ее логическим продолжением. Для освоения данной темы обучающиеся должны хорошо владеть понятием «Определенный интеграл» и уметь находить его, используя формулу Ньютона-Лейбница.
Содержание
| Этап урока | Методы обучения | Время |
| 1. Самоопределение к деятельности (оргмомент) |
| 2 мин |
| 2. Актуализация опорных знаний | - машинный программированный контроль; - фронтальный опрос; - практический метод. | 10 мин |
| 3. Формирование новых знаний и способов действий | - продуктивный метод; - практический метод. | 10 мин |
| 4. Применение знаний, формирование умений | - практический метод | 20 мин |
| 5. Подведение итогов урока. Задание на дом |
| 3 мин |
Особенностью данного урока является применение информационно-коммуникационных технологий.
При проверке знаний по теме «Определенный интеграл» используется машинный программированный контроль, который позволяет за относительно небольшой промежуток времени проверить качество знаний большого числа студентов, в данном случае это 10 учеников.
При изучении нового материала используется презентация PowerPoint с элементами мультимедиа.
Использование интерактивной доски на этом этапе урока позволяет сократить время на построение графиков, запись формул и определений. Материал становится более наглядным и более доступным.
Бòльшая часть урока отводится на закрепление полученных теоретических знаний. Закрепление материала заключается в решении задач из электронного учебного пособия.
При выполнении домашнего задания обучающиеся будут использовать ресурсы сети Интернет, что одновременно способствует совершенствованию навыков работы с цифровыми образовательными ресурсами и повышает интерес к предмету, а, следовательно, способствует совершенствованию достижений навыков образовательных результатов.
Ожидаемые результаты
Сформированные знания понятия «криволинейная трапеция», формулы площади криволинейной трапеции, способов нахождения площадей различных фигур.
Сформированные навыки применения определенного интеграла к вычислению площади криволинейной трапеции путем вычитания площадей.
Цели – это конечный результат. На мой взгляд, цели и ожидаемый результат совпали.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
| Методы обучения | Название | Обоснование |
| - дедуктивный метод
- практический метод | - способствует быстрому прохождению материала
- эффективно содействует отработке практических умений и навыков | |
| Виды контроля | - машинный контроль; - стимулирующий; - диагностический. | |
| Что контролируется? | - знание понятий: «интеграл», «определенный интеграл», «формула Ньютона-Лейбница», «пределы интегрирования», «подинтегральная функция»; «формула площади криволинейной трапеции»; - умение находить определенный интеграл; - навыки применения определенного интеграла к вычислению площади криволинейной трапеции. | |
| Приемы контроля | - наблюдение; - устный контроль; - письменный контроль. | |
| Ожидаемые результаты | Сформированные знания понятия «криволинейная трапеция», формулы площади криволинейной трапеции, способов нахождения площадей различных фигур. Сформированные навыки применения определенного интеграла к вычислению площади криволинейной трапеции. | |
Цели урока:
1. Образовательные:
а) закрепить навыки нахождения определенного интеграла;
б) обеспечить усвоение студентами понятия «криволинейная трапеция» и различных способов нахождения площади криволинейной трапеции;
в) отработать навыки нахождения площади криволинейной трапеции путем вычитания площадей.
2. Развивающие:
а) развитие психических качеств обучающихся (умений применять полученные знания на практике);
б) развитие познавательных умений и мышления (выделять главное, анализировать, сравнивать, определять и объяснять понятия).
3. Воспитательные:
а) воспитание положительного отношения к знаниям;
б) воспитание дисциплинированности;
в) воспитание эстетических взглядов.
Тип урока: комбинированный.
Вид урока: беседа
Оборудование:
компьютерный класс,
интерактивная доска,
проектор,
карточки-задания.
Демонстрационный материал:
презентация PowerPoint;
электронное учебное пособие с элементами мультимедиа.
Межпредметные связи: геометрия, физика
Проект учебного занятия
| Тема учебного занятия: | Применение определенного интеграла для нахождения площади криволинейной трапеции | ||
| Тип урока | комбинированный | ||
| Цели обучающегося: | а) закрепить навыки нахождения определенного интеграла; б) усвоить понятие «криволинейная трапеция»; в) усвоить различные способы нахождения площади криволинейной трапеции; г) отработать навыки нахождения площади криволинейной трапеции. | ||
| Этапы учебного занятия: | Деятельность педагога | Деятельность обучающегося | |
| I.Самоопределение к деятельности (оргмомент) | Проверяет готовность обучающихся к уроку; отмечает отсутствующих; формулирует тему и цели урока | Готовятся к восприятию материала | |
| II. Актуализация опорных знаний | Обеспечивает повторение знаний и умений, полученных на предыдущих уроках: 1. компьютерный тест - вопросы прилагаются; (приложение №1) 2. Вопросы: 1). Сформулируйте формулу Ньютона-Лейбница. 2) Вычислите интеграл 3) Сформулируйте определение определенного интеграла. 4)Историческая справка. (слайд 1) 5) В чем заключается геометрический смысл определенного интеграла? |
1. компьютерное тестирование – 10 чел.
2. фронтальный опрос с решением примеров – 5 чел.
1)
2) Решают пример на доске и в тетрадях
3) Приращение F(b)-F(a) любой из первообразных функций F(x) + C при изменении аргумента от х=а до х=b называется определенным интегралом от а до b функции f(x):
Рассказывает историческую справку.
5) Определенный интеграл – это площадь фигуры, сверху ограниченной графиком функции f(x), снизу - осью абсцисс, по бокам - прямыми х=а и х=b. | |
| III. «Открытие» новых знаний | 1) Формулирует тему урока (слайд 2) | Записывают тему урока в тетрадях. | |
| 2) Формулирует определение криволинейной трапеции (слайд 3,4,5,6) | Делают чертеж и записывают определение в тетрадях. | ||
| 3) Записывает формулу площади криволинейной трапеции (слайд7) | Записывают формулу в тетрадях.
| ||
| 4) Приводит способы нахождения площадей различных фигур (слайды 7а,8,9,10,11) | Отвечают на поставленные вопросы. Записывают в тетрадях. | ||
| IV. Применение знаний, формирование умений | 1) Решает пример на ИД (15.ехе, практика, задача 2) | Записывают решение в тетрадях. | |
|
| 2) Руководит решением примеров на ИД (15.ехе. практика, задача1) (16.ехе, задача 3) | Решают примеры на ИД и записывают их в тетрадях. | |
|
| 3) Контролирует написание самостоятельной работы.(приложение 5) | На выданных листах решают дифференцированную самостоятельную работу. | |
| V. Подведение итогов. Д/задание. | Выставление оценок. Домашнее задание: гл.10, стр. 199-204, зад. 10.6 (4,5,10) | Записывают домашнее задание в тетрадях. | |
| Список учебных элементов содержания | № | Название учебного элемента | |
| 1. 2. 3. 4.
5. 6. | Интеграл Определенный интеграл Формула Ньютона-Лейбница Геометрический смысл определенного интеграла Криволинейная трапеция Площадь криволинейной трапеции | ||
Приложение1
Вопросы компьютерного тестирования
Чему равен нижний предел интегрирования в интеграле
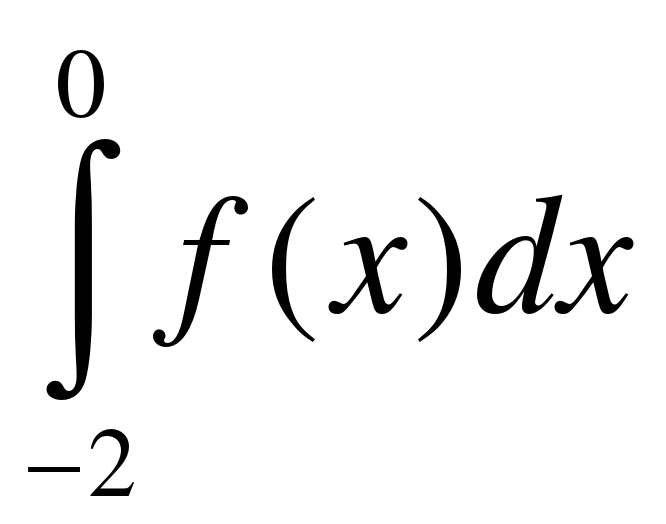 (-2)
(-2)Данный интеграл
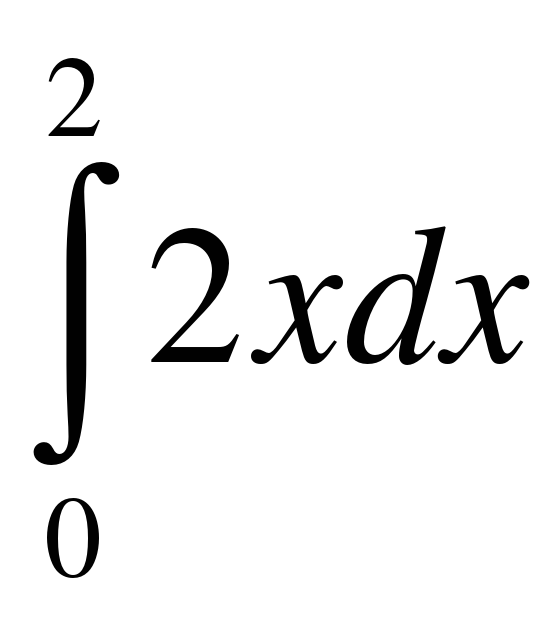 равен:
равен:
а) 0
б) -4
в) 4
г) 8
В данном интеграле
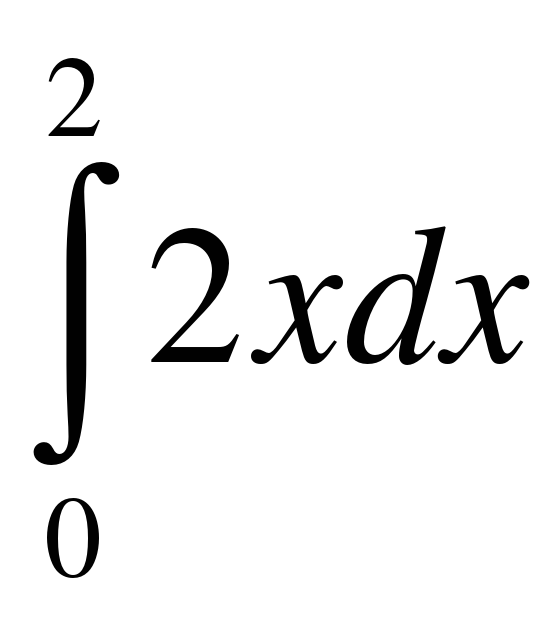 подинтегральная функция равна:
подинтегральная функция равна:
а) 2х
б) dх
в) 0
г) 2
Данный интеграл
 равен:
равен:
а) 1
б) С
в) 0
г) зависит от подинтегральной функции
Выражение данного вида
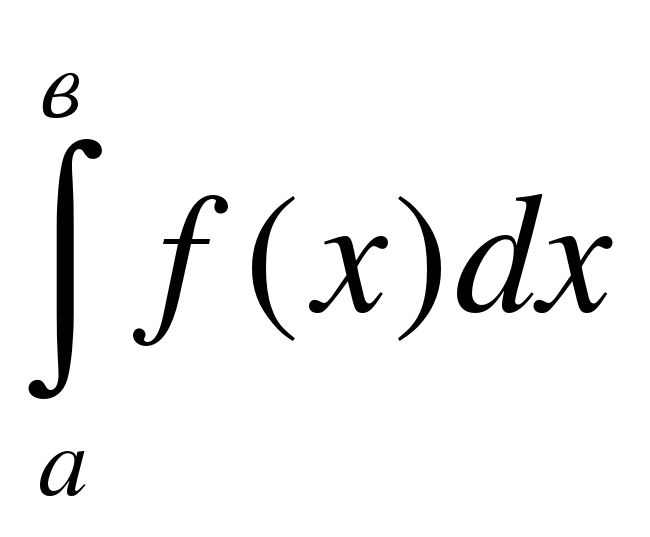 называется:
называется:
а) определенный интеграл
б) неопределенный интеграл
в) интегралом функции
г) дифференциалом
6. Определенный интеграл вычисляется с помощью формулы:
а) Лейбница
б) Ньютона
в) Лагранжа
г) Ньютона-Лейбница
7. При перестановке пределов интегрирования в определенном интеграле, интеграл ...
а) не изменится
б) увеличится в 2 раза
в) поменяет знак
г) подинтегральная функция изменится на обратную
слайд 1


Слайд3

 Слайд7
Слайд7

С лайд8
лайд8

Приложение 4






Приложение 5
Самостоятельная работа
Н
 айдите площадь криволинейной трапеции, изображенной на рисунке:
айдите площадь криволинейной трапеции, изображенной на рисунке:
Н
y
айдите площадь фигуры, изображенной на рисунке:
0 у = sin x х 0 



![]()

![]()



Н






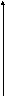
х
y
айдите площадь фигуры, ограниченной прямой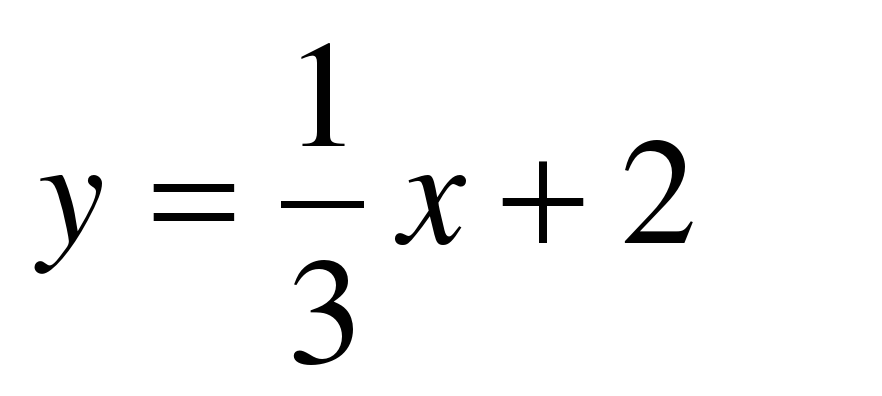 и параболой
и параболой 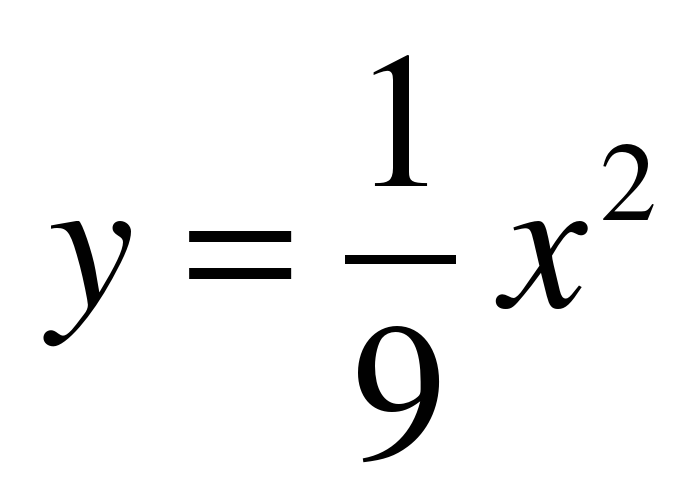
Оценка «3» ставится за правильное решение задания №1
Оценка «4» ставится за правильное решение задания №2
Оценка «5» ставится за правильное решение задания №3
Используемая литература
Башмаков М.И. Математика. Учебник для обучающихся в учреждениях начального и среднего профессионального образования. М.: Издательский центр “Академия”, 2013.
Башмаков М.И. Математика. Задачник для обучающихся в учреждениях начального и среднего профессионального образования. М.: Издательский центр “Академия”, 2013.
Башмаков М.И. Математика. Сборник задач для обучающихся в учреждениях начального и среднего профессионального образования. М.: Издательский центр “Академия”, 2013.
Башмаков М.И. Математика. Методическое пособие для учреждений начального и среднего профессионального образования. М.: Издательский центр “Академия”, 2013.
Колмогоров А.Н. и др. Алгебра и начала анализа. 10 (11) кл. М.: Просвещение, 2008.
Интернет- ресурсы:
http://festival.1september.ru/
http://www.uchportal.ru
http://allmath.ru/
Методическую разработку подготовила
Сорокина Л.В.- преподаватель математики, высшая квалификационная категория
Конспект урока
Тема: «Применение определенного интеграла для нахождения площади криволинейной трапеции»
Цели:
Воспитательные:
воспитание положительного отношения к знаниям;
воспитание дисциплинированности;
воспитание эстетических взглядов.
Развивающие:
развитие психических качеств студентов: мышления, умений применять полученные знания на практике;
развитие познавательных умений (выделять главное, вести конспект);
развитие общетрудовых и политехнических умений;
развитие умений учебного труда (читать, писать);
развитие воли, самостоятельности).
Образовательные:
закрепить навыки нахождения определенного интеграла;
добиться усвоения студентами понятия «криволинейная трапеция»;
обеспечить усвоение студентами различных способов нахождения площади криволинейной трапеции;
отработать навыки нахождения площади криволинейной трапеции.
Тип: комбинированный
План урока
I. Организационный момент - 2 мин.
II. Актуализация опорных знаний - 10 мин.
III. Объяснение нового материала - 10 мин.
IV. Применение знаний, формирование умений - 20 мин.
V. Подведение итогов, домашнее задание - 3 мин.
ХОД УРОКА:
I. Оргмомент
II. Актуализация опорных знаний
Вспомним материал предыдущих уроков по теме «Определенный интеграл».
Для проведения контроля нам необходимо назначить консультанта. Есть желающие? Консультант выставит оценки за тестирование. Напоминаю, оценка «5» ставится за 90-100% правильных ответов, «4» - 70-90%, «3» - 50-70%, будем надеется, что меньше 50% никто не наберет.
Пока ребята отвечают на вопросы теста, мы ответим на вопросы у доски.
1 . Записать формулу Ньютона-Лейбница.
. Записать формулу Ньютона-Лейбница.
А теперь примени ее для нахождения определенного интеграла.
(14.ехе, задание 1, пример 1)

2. Что такое определенный интеграл?
Здесь тоже фигурирует формула Ньютона-Лейбница. Найди определенный интеграл по этой формуле. (14.ехе, задание 1, пример 2)
Формула Ньютона-Лейбница… Откуда взялась эта формула. Вам было дано домашнее задание найти историческую справку. Кто нам об этом расскажет? (Историческая справка, слайд 1)
(Консультант выставляет оценки студентам).
3. В чем заключается геометрический смысл определенного интеграла?
III. Объяснение нового материала
1) И так, определенный интеграл – это площадь фигуры, ограниченной графиком положительной функции f(х), осью абсцисс и прямыми х=а, х=в. Такая фигура называется криволинейной трапецией.
Сегодня мы узнаем, что такое криволинейная трапеция и рассмотрим различные способы нахождения ее площади с помощью определенного интеграла.
Запишите в тетрадях тему урока: «Площадь криволинейной трапеции» (слайд 2
2) Что же такое криволинейная трапеция?
Пусть на отрезке [a; b] оси абсцисс определена функция у=f(х)0. Фигура, ограниченная графиком этой функции, отрезком [a; b] и прямыми х=а, х=b называется криволинейной трапецией (слайд 3,4,5.6). В тетрадях сделайте чертеж и запишите определение.
3) Исходя из геометрического смысла определенного интеграла, площадь криволинейной трапеции равна: ![]() (слайд 7), где пределы интегрирования – это отрезок [a; b] оси абсцисс, на котором мы рассматриваем трапецию, а подинтегральная функция – та, график которой ограничивает трапецию сверху.
(слайд 7), где пределы интегрирования – это отрезок [a; b] оси абсцисс, на котором мы рассматриваем трапецию, а подинтегральная функция – та, график которой ограничивает трапецию сверху.
4) Рассмотрим следующие фигуры.
а) (слайд 7а). Фигура ограничена графиком функции у=f(x), отрезком [a, в] и прямыми х=а, х=в. Заштрихуйте фигуру, ограниченную этими линиями.
Как можно определить площадь этой фигуры? (Проинтегрировать функцию у=f(x) на отрезке [a, в]).
Но эта фигура находится «ниже» оси Ох и вычисляя интеграл мы получим отрицательное значение, чего не может быть при вычислении площади.
Следовательно, площадь равна: ![]()
Запишите в тетрадях правило нахождения площади рассмотренной фигуры.
б) (слайд 8). Покажите криволинейную трапецию, ограниченную графиками функций g(x) и f(x).
На каком отрезке рассматривается данная фигура?
Как найти концы этого отрезка? (Концы отрезка – это точки пересечения графиков. Чтобы найти абсциссы этих точек функции надо приравнять).
А как вычислить площадь этой фигуры? (Эта фигура является разностью фигур с площадями S1 и S2).
Следовательно, S=S1–S2
Запишите в тетрадях правило нахождения площадей рассмотренных фигур. (слайд 9,10,11)
IV. Применение знаний, формирование умений
1) А теперь применим полученные знания на практике.
Решим задачу вместе со мной. (15.ехе, практика, задача 2). Для определения площади фигуры построим эту фигуру.
Найдем точки, в которых графики пересекаются, для этого приравняем функции, получаем уравнение х2 – 2х = 0. Отсюда следует, что х1 = 0, х1 =3.
Графиком функции у = х2 – 2х является парабола, ветви вверх, пересекает ось Ох в точках 0 и 2. График функции у = х – прямая. Построим эти графики. Получили ограниченную этими графиками фигуру. Так как сверху фигура ограничена графиком у = х, снизу - у = х2 – 2х, то искомая площадь вычисляется как разность интегралов:  , по свойству интегралов получаем:
, по свойству интегралов получаем:  . Приведем подобные, получаем подинтегральную функцию
. Приведем подобные, получаем подинтегральную функцию
- х2 + 3х. Находим первообразную: - х3 /3 + 3х2 /2.
Подставим верхний предел интегрирования:
![]()
2) Посмотрим, как получится у вас.
а) (15.ехе, практика, задача 1) Прочитать условие. Кто желает решить задачу у доски?
б) (16.ехе, практика, задача 3) Прочитать условие. Кто желает решить задачу у доски?
3) Сегодня мы познакомились с понятием «криволинейная трапеция», узнали, как можно вычислять ее площадь.
А теперь посмотрим, как вы разобрались в этом материале (Самостоятельная работа)
V. Подведение итогов, домашнее задание
Собрать выполненные самостоятельные работы.
Кто выполнял задание на «5», кто – на «4», кто – на «3»? Оценки за самостоятельную работу вы узнаете на следующем уроке, а сегодня на уроке получили оценки:
а) тест – 10 чел.
б) за ответ у доски – 3 чел.
в) за решение примеров - 2 чел.
Домашнее задание:
гл.10, стр. 199-204, зад. 10.6 (4,5,10)
Дополнительное задание:
Найти в Интернет примеры практического применения вычисления площади криволинейной трапеции.
Используемая литература
Башмаков М.И. Математика. Учебник для обучающихся в учреждениях начального и среднего профессионального образования. М.: Издательский центр “Академия”, 2013.
Башмаков М.И. Математика. Задачник для обучающихся в учреждениях начального и среднего профессионального образования. М.: Издательский центр “Академия”, 2013.
Башмаков М.И. Математика. Сборник задач для обучающихся в учреждениях начального и среднего профессионального образования. М.: Издательский центр “Академия”, 2013.
Башмаков М.И. Математика. Методическое пособие для учреждений начального и среднего профессионального образования. М.: Издательский центр “Академия”, 2013.
Колмогоров А.Н. и др. Алгебра и начала анализа. 10 (11) кл. М.: Просвещение, 2008.
Интернет
Материалы для посещающего урок
Основные критерии эффективности
применения ИКТ на уроке
Безусловно, что умелое сочетание традиционных и информационных средств зависит от квалификации и мастерства преподавателя, методики, которую он применяет. Но грамотное использование средств ИТ зависит и от знаний преподавателем педагогических основ по информатизации уроков.
Основные критерии эффективности применения ИКТ на отдельных этапах урока следующие:
целесообразность;
соблюдение санитарных норм;
соблюдение баланса между средствами ИКТ и средствами человеческого общения;
соответствие материала на ЦОРе возрастным особенностям обучающихся;
четкость инструктажа каждого задания;
активность обучающихся;
ощущение комфортности;
рефлексия.
Все эти критерии должен учитывать преподаватель при составлении урока, а завуч должен обратить внимание насколько успешно преподаватель руководствуется этими критериями.
ТИПОВАЯ КАРТА ПОСЕЩЕНИЯ УРОКА
Дата посещения
Преподаватель
Предмет
Группа
Классный руководитель
На уроке присутствовали:
1. Общая информация об уроке
1.1. Причина посещения урока (отмечается одна из причин)
плановое посещение;
внеплановое посещение (указывается причина внепланового посещения).
1. 2. Цель посещения урока (отмечается одна из целей)
знакомство с преподавателем;
комплексное наблюдение за работой преподавателя;
наблюдение за работой преподавателя в связи с определенной проблемой или решением определенной задачи (указывается проблема или задача)
наблюдение за работой класса, отдельных обучающийся; диагностика затруднений преподавателя;
диагностика затруднений группы;
контроль (указывается форма контроля),
подготовка к аттестации;
аттестация;
психолого-педагогическое наблюдение;
другое (указывается цель посещения).
1. 3. Общая характеристика урока
1.3.1 .Тема урока: ___________________________________
1.3.2. Место урока в системе уроков .
1.3.3. Тип урока .
1.3.4. Цель урока .
1.3.5. задачи урока .
1.3.6. оборудование и наглядные пособия, использованные на уроке (в том числе использование доски)
1.3.7. Контроль и оценивание умений, знаний и навыков обучающихся
1.3.8. Работа с тетрадями обучающийся ______
2. Краткий конспект урока с комментариями,
замечаниями, рекомендациями
| Этап урока, его краткое содержание | Деятельность учащихся | Деятельность преподавателя | Комментарии, замечания, рекомендации |
|
|
|
|
|
3. Анализ урока
3.1. Исчерпанность темы
- исчерпана полностью; - исчерпана не полностью;
- практически не исчерпана; - не исчерпана.
Замечания, рекомендации ___________________________________________
____________________________________________________________________________________________________________________________________
3.2. Степень реализации цели урока
цель реализована;
цель реализована не полностью;
цель не реализована.
3.3. Степень выполнения задач
- задачи выполнены полностью; - все задачи выполнены частично
- выполнены не все задачи; - задачи не выполнены.
Замечания, рекомендации ____________________________________________
__________________________________________________________________
3.4 Характер отбора содержания материала урока
- научность, значимость теорети- - привлекательность;
ческая; - дифференцированность;
- значимость практическая; - логичность;
- доступность; - наглядность;
- соответствие возрастным и ин- - другое (указать, что),
теллектуальным возможностям
обучающихся;
3.5. Характеристика форм работы
- соответствие цели, задачам и - сменяемость;
содержанию; - другое (указать, что).
- разнообразие;
- чередуемость;
3.6. Логичность композиции урока
композиция урока логична;
композиционная логика отсутствует.
в композиции урока имеются нарушения логики;
Замечания, рекомендации
_________________________________________________________________
3.7. Развивающая характеристика урока, развитие устной речи школьников
3.8. Психологическая характеристика урока (психологический климат занятия)
Параметры оценки
| | + | +/- | - | ? |
| Разнообразие приемов психологического воздействия и стимулирования активности обучающихся |
|
|
|
|
| Разумное соотношение нагрузки на память и мышление |
|
|
|
|
| Разумное соотношение воспроизводящей и творческой деятельности |
|
|
|
|
| Разумное соотношение знаний «в готовом виде» и их самостоятельного поиска |
|
|
|
|
| Разумное соотношение побуждения обучающихся к деятельности и корректного принуждения школьников |
|
|
|
|
| Педагогический такт преподавателя |
|
|
|
|
| Психологический климат в классе |
|
|
|
|
| Рабочее самочувствие преподавателя на уроке самочувствие обучающихся на уроке |
|
|
|
|
| Учет возрастных и психофизических особенностей отдельных обучающихся и класса в целом |
|
|
|
|
| Другое |
|
|
|
|
Примерная схема анализа урока с использованием
информационно - коммуникационных технологий
3.9 Анализ эффективности использования средств ИКТ
|
| + | +/- | - | ? | |
| Актуальность использования средств ИКТ |
|
|
|
| |
| Вид используемых на уроке средств ИКТ |
| ||||
|
|
| |||
|
|
| |||
|
|
| |||
|
|
| |||
3.9.1 Презентация
Текстовое оформление
- Структура - Формат
- Объем - Подача текстовой информации
Эстетика оформления слайдов
- Цветовая гамма - Анимация
- Звуковое сопровождение
Видеоинформация
- Время - Обратная связь
3.9.2 Цифровые образовательные ресурсы (ЦОР)
ЭУИ
- Соответствие возрастным осо- - Дружественный интерфейс
бенностям учащегося
- Удобная навигация
Интернет
|
| Соответствие теме урока | Соответствие возрастным особенностям обучающихся | Достоверность информации |
| Поиск инфор-мации в WWW |
|
|
|
| Тестирование on-line |
|
|
|
| Виртуальные экскурсии |
|
|
|
3.9.3 Соблюдение санитарно-гигиенических требований
4. Анализ домашнего задания
| По объему | По содержанию | По форме | Примечания, замечания |
|
|
| |
5. Оценка урока
Оценка урока учителем (самооценка)
Замечания и предложения
Заключение
Анализ любого урока представляет собой комплексный подход, в котором психологический, педагогический, содержательный, методический и предметный аспекты тесно взаимосвязаны. Сам по себе анализ урока как процесс осознания и самопознания формирует у учителя аналитические способности, развивает интерес и определяет необходимость изучения проблем обучения и воспитания. Умение проводить наблюдения за сложными педагогическими явлениями, анализировать их, обобщать и делать научно обоснованные выводы, служит действенным средством совершенствования профессионально-педагогического мастерства.



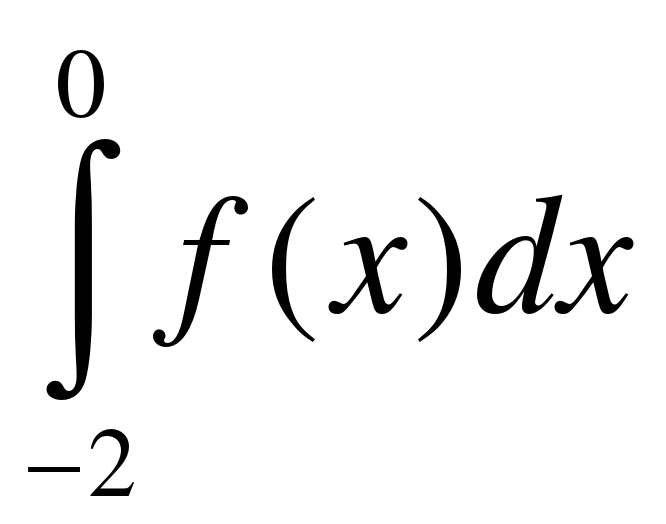 (-2)
(-2)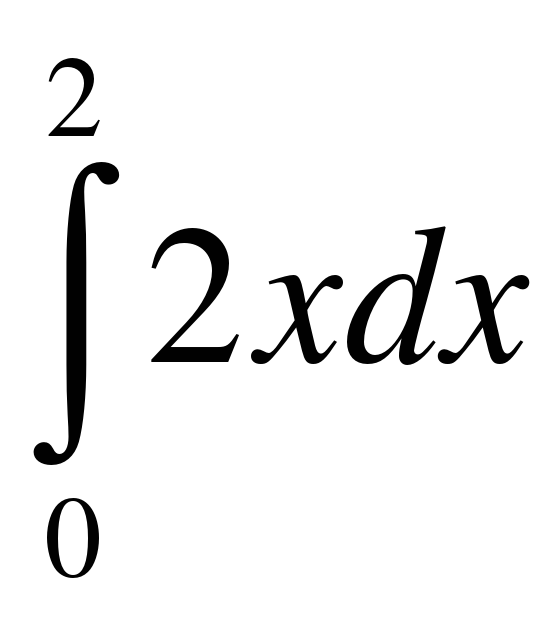 равен:
равен: айдите площадь криволинейной трапеции, изображенной на рисунке:
айдите площадь криволинейной трапеции, изображенной на рисунке: