17.11.20
УРОК АЛГЕБРЫ В 9 КЛАССЕ
.
Эпиграф урока:
«… руководить ходом своих мыслей, начиная с предметов простейших
и легко познаваемых, и восходить мало-помалу, как по ступеням до познания наиболее сложных…»
Р. Декарт
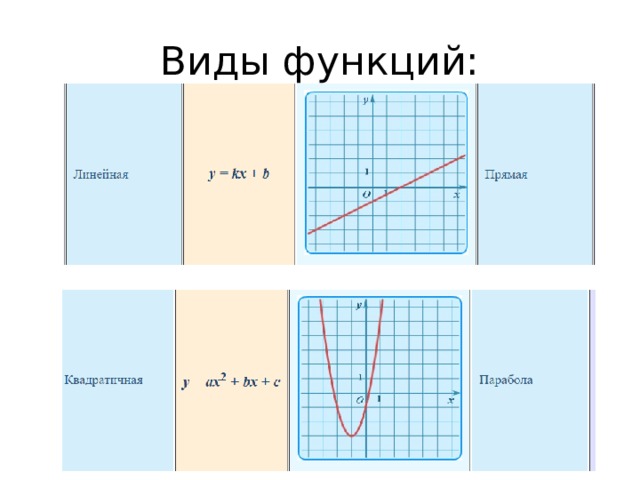
Виды функций:
a- класс
в-год обучения в КК
с- кол-во мальчиков в классе
d- кол-во девочек в классе
Тема:
«Функции у = х n (n Є N), их свойства и графики».
Задача:
Научиться строить графики функции у = х n (n Є N) и изучить их свойства».
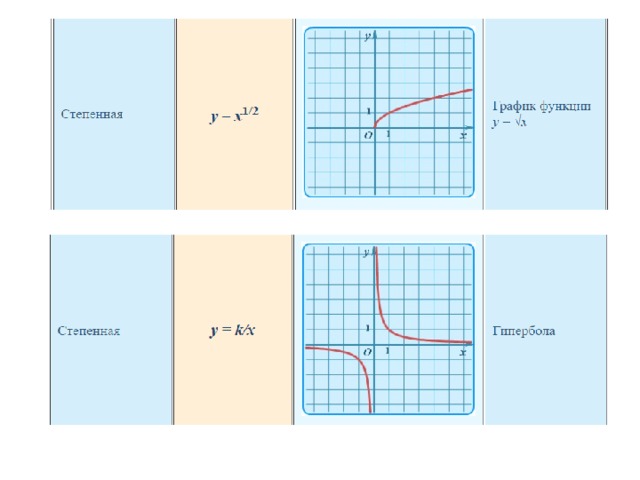
Определение
Функцию у = х n , где n = 1, 2, 3, 4, 5, …, называют степенной функцией с натуральным показателем.
Исследование функций
0, при х…, у4. Монотонность (промежутки возрастания и убывания) 5. Определить четность или нечетность функции. 6. Определить непрерывность функции. Определить ограниченность функции. 7. Указать наибольшее и наименьшее значение функции." width="640"
План исследования функций:
А)Построить график с помощью таблицы
Б) описать его свойства
1. D(f) и Е(f) .
2. Нули функции, у=0, при х=…
3. Промежутки знакопостояства.
у0, при х…, у
4. Монотонность (промежутки
возрастания и убывания)
5. Определить четность или нечетность функции.
6. Определить непрерывность функции.
Определить ограниченность функции.
7. Указать наибольшее и наименьшее значение функции.
0, при х0; у4. возрастает на всей области определения; 5. Нечетная, не ограничена ни снизу, ни сверху; 6. нет ни наибольшего, ни наименьшего значения; 7. функция непрерывна. ." width="640"
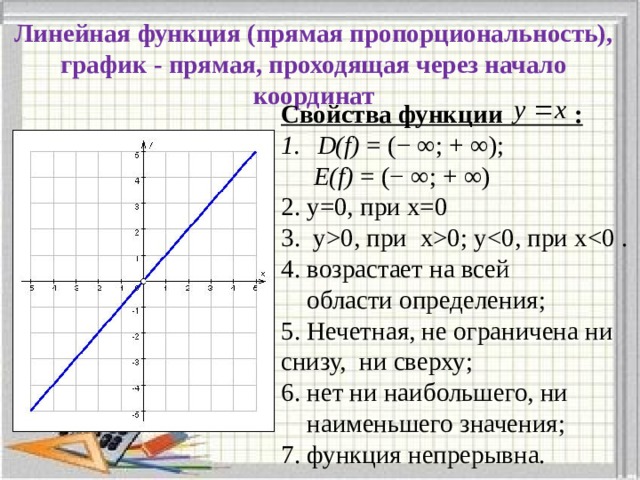
Линейная функция (прямая пропорциональность), график - прямая, проходящая через начало координат
Свойства функции :
- D(f) = (− ∞; + ∞);
Е(f) = (− ∞; + ∞)
2. у=0, при х=0
3. у0, при х0; у
4. возрастает на всей
области определения;
5. Нечетная, не ограничена ни снизу, ни сверху;
6. нет ни наибольшего, ни
наименьшего значения;
7. функция непрерывна.
.
0, при х0; х4. убывает (− ∞; 0], возрастает [0; + ∞) 5. чётная, ограничена снизу 6. У наим . = 0, У наиб . - не существует; 7. функция непрерывна." width="640"
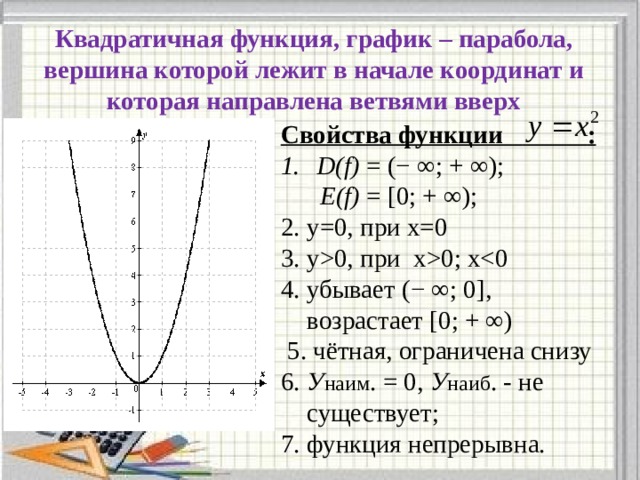
Квадратичная функция, график – парабола, вершина которой лежит в начале координат и которая направлена ветвями вверх
Свойства функции :
- D(f) = (− ∞; + ∞);
Е(f) = [0; + ∞);
2. у=0, при х=0
3. у0, при х0; х
4. убывает (− ∞; 0],
возрастает [0; + ∞)
5. чётная, ограничена снизу
6. У наим . = 0, У наиб . - не
существует;
7. функция непрерывна.
На какие группы можно разделить все функции?
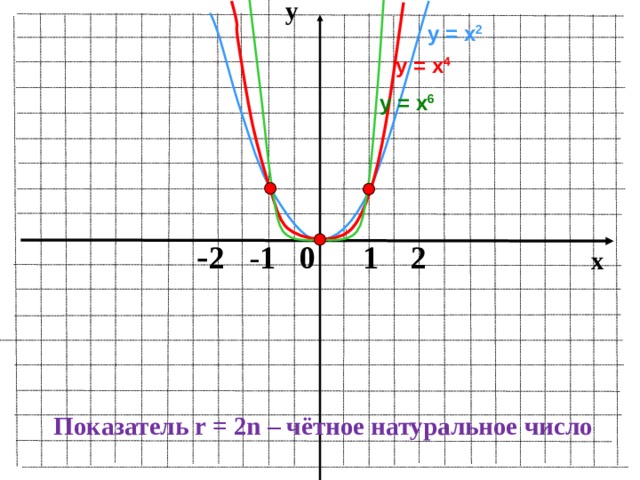
y
у = х 2
у = х 4
у = х 6
- 2 - 1 0 1 2
x
Показатель r = 2n – чётное натуральное число
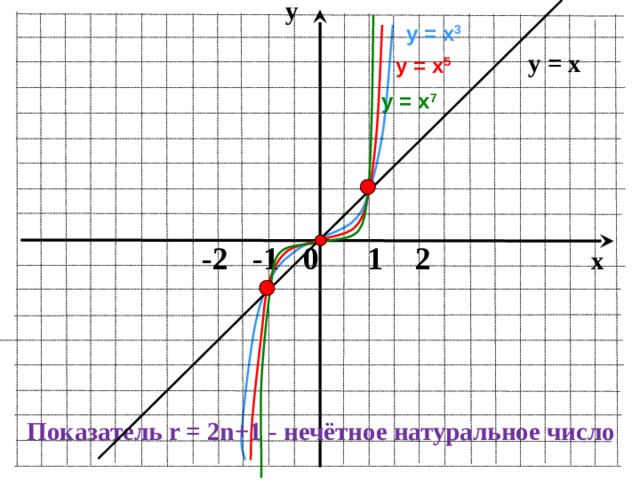
y
у = х 3
у = х
у = х 5
у = х 7
-2 -1 0 1 2
x
Показатель r = 2n+1 - нечётное натуральное число
Ответ на поставленный вопрос найден!
Вывод:
График функции и её свойства такие же как у функции .
у
Отметьте на десятибалльной шкале значком ваше эмоциональное ощущение на уроке и значком - степень усвоения нового материала.
10
9
8
7
6
5
4
3
2
1
0
0
х
Домашнее задание:
Заполнить карточку.
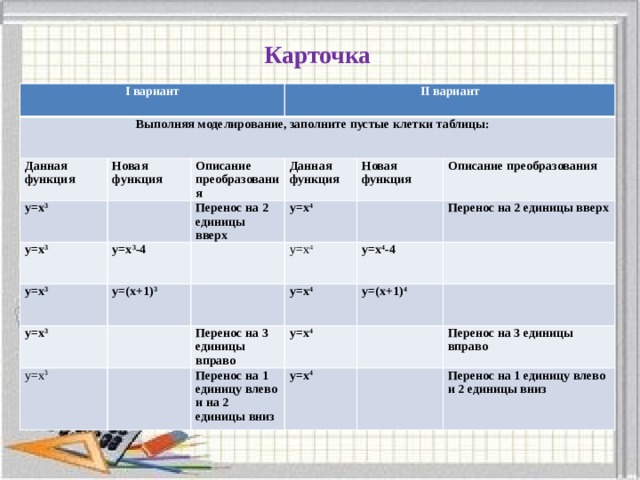
Карточка
I вариант
Выполняя моделирование, заполните пустые клетки таблицы:
Данная функция
II вариант
Новая функция
y=x 3
Описание преобразования
y=x 3
Данная функция
Перенос на 2 единицы вверх
y=x 3 -4
y=x 3
y=x 4
Новая функция
y=(x+1) 3
y=x 3
Описание преобразования
y=x 4
y=x 3
Перенос на 2 единицы вверх
Перенос на 3 единицы вправо
y=x 4 -4
y=x 4
y=x 4
y=(x+1) 4
Перенос на 1 единицу влево и на 2 единицы вниз
y=x 4
Перенос на 3 единицы вправо
Перенос на 1 единицу влево и 2 единицы вниз
Спасибо за урок !
