

Проверка домашнего задания
- Выучить определение и свойства показательной функции и экспоненты.
- Построить графики функций
у=(1/3) x у=4 x -2

Задания на повторение
 0 и а ǂ 1 Функцию, заданную формулой у= log a x, называют логарифмической функцией с основанием а" width="640"
0 и а ǂ 1 Функцию, заданную формулой у= log a x, называют логарифмической функцией с основанием а" width="640"
Логарифмическая функция
у= log a x
- Пусть а 0 и а ǂ 1
- Функцию, заданную формулой
у= log a x,
называют логарифмической функцией с основанием а
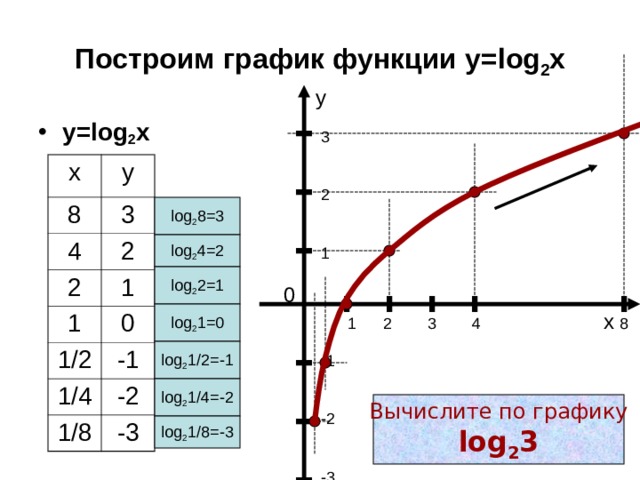
Построим график функции у= log 2 x
у
- у= log 2 x
3
2
1
х
у
8
3
4
2
2
1
1
0
1/2
-1
1/4
-2
1/8
-3
log 2 8=3
log 2 4=2
log 2 2=1
0
х
log 2 1=0
1 2 3 4 8
log 2 1/2=-1
-1
-2
-3
log 2 1/4=-2
Вычислите по графику
log 2 3
log 2 1/8=-3

Построим график функции у= log 1/2 x
- у= log 1/2 x
х
у

Свойства функции у= log а x
- 1) Область определения логарифмической функции Д(у)=(0; +∞)
- 2) Область значений логарифмической функции Е(у)=(-∞;+∞)
- 3) Логарифмическая функция на всей области определения возрастает при а 1 и убывает при 0

Найдите область определения логарифмической функции
- у= log 4 (10-5х)
- Решение:
- Д(у)=(0; +∞)
- 10-5х 0;
- -5х -10;
- х
- х
- Ответ: Д(у)=(-∞; 2)
- log 5 (3х-27)
 0; 9-х 2 =0; -х 2 =-9; х 2 =9; х= ± 3; Ответ: Д(у)=(-3; 3) log 7 (х 2 -16) -3 3" width="640"
0; 9-х 2 =0; -х 2 =-9; х 2 =9; х= ± 3; Ответ: Д(у)=(-3; 3) log 7 (х 2 -16) -3 3" width="640"
Найдите область определения логарифмической функции
- log 5 (9-х 2 )
- Решение:
- Д(у)=(0; +∞)
- 9-х 2 0; 9-х 2 =0;
- -х 2 =-9; х 2 =9;
- х= ± 3;
- Ответ: Д(у)=(-3; 3)
- log 7 (х 2 -16)
-3 3

Постройте график функции у= log 3 ( x -2) и перечислите ее свойства

Постройте схематично график возрастающей и убывающей логарифмических функции

Постройте схематично графики функций у= log 3 х и у= log 5 х

Укажите какие из данных функции убывающие, а какие возрастающие.
- у= log 4 x ;
- у= log 0,6 x ;
- у= log 1/3 x ;
- у= log 12 x ;
- у= log 8/7 x ;
- у= lnx ;
- у= lgx ;

Перечислите свойства
- Логарифмов
- log а 1=
- log а а=
- log а ху=
- log а х/у=
- log а х р =
- Логарифмической функции
- Д(у)=
- Е(у)=
- Функция возрастает при
- Функция убывает
при

Запишите общий вид логарифмической и показательной функции

Домашнее задание
- 1) Выучить определение и свойства логарифмической функции.
- 2) Знать свойства логарифмов.
- 3) Найти область определения функций
- а) у= log 3 (8-4х)
- б) у= log 5 (х 2 -64)
- в) у= log 0,9 (х 2 -3х+2)
- 4) Решите уравнение 7 2х-3 =( 1/343) 9-х







