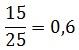Практикум по решению вероятностных задач

Ответы теория вероятностей

1. 0,1

2.  0,1

3.  0,17

4.  0,48

5.  0,999

6.  0,5

7. 0,5

8. 0,98

9.  0,04

10.  0,5

11. 0,82

12.  0,8

13.  0,375

14.  0,5

15.  0,99

16.  0,4

17.  0,97

18.  0,96

19. 0,375

20.  0,2

21.  0,9964

22. 0,4

23. 0,6

24.  0,25

25.  0,125

26.  0,14

27.  0,6

28.  0,58

29.  0,505

30.  0,25

31.  0,2

32. 0,25

33. 0,012

34. 0,26

35. 0,25

36.  0,16

37.  0,15

ТЕОРИЯ ВЕРОЯТНОСТЕЙ

1. В классе 7 мальчиков и 14 девочек. 1 сентября случайным образом определяют двух дежурных на 2 сентября, которые должны приготовить класс к занятиям. Найдите вероятность того, что будут дежурить два мальчика. 

Решение: Вероятность, того что первый дежурный будет мальчик равна 7 / 21 (т.к. всего в классе 7 + 14 = 21 учащихся и  из них 7 мальчиков).
Вероятность, того что и второй дежурный будет мальчиком равна 6 / 20 (т.к. всего 6 мальчиков в оставшихся 20 учащихся) .
Тогда вероятность, того  что, оба дежурные будут мальчиками равна: (7/21) · (6/20)=0,1

Ответ: 0,1

2. В фирме такси в дан­ный мо­мент сво­бод­но 10 машин: 5 чер­ных, 1 жел­тая и 4 зе­ле­ных. По вы­зо­ву вы­еха­ла одна из машин, слу­чай­но ока­зав­ша­я­ся ближе всего к за­каз­чи­ку. Най­ди­те ве­ро­ят­ность того, что к нему при­е­дет жёлтое такси.

Решение: Ве­ро­ят­ность того, что к за­каз­чи­ку при­е­дет жёлтое такси равна:
                                                                      1/10=0,1

Ответ: 0,1

3. В слу­чай­ном экс­пе­ри­мен­те бро­са­ют две иг­раль­ные кости. Най­ди­те ве­ро­ят­ность того, что в сумме вы­па­дет 7 очков. Ре­зуль­тат округ­ли­те до сотых.

Решение: Ко­ли­че­ство ис­хо­дов, при ко­то­рых в ре­зуль­та­те брос­ка иг­раль­ных ко­стей вы­па­дет 7 очков, равно 6:
1+6, 2+5, 3+4, 4+3, 5+2, 6+1.
Каж­дый из ку­би­ков может вы­пасть ше­стью ва­ри­ан­та­ми, по­это­му общее число ис­хо­дов равно
6 · 6 = 36.
Сле­до­ва­тель­но, ве­ро­ят­ность того, что в сумме вы­па­дет 7 очков, равна
6 / 36 = 1 / 6 ≈ 0,1666... ≈ 0,17

Ответ: 0,17

4. В сбор­ни­ке би­ле­тов по био­ло­гии всего 25 би­ле­тов, в 12 из них встре­ча­ет­ся во­прос по круглым червям. Най­ди­те ве­ро­ят­ность того, что в слу­чай­но вы­бран­ном на эк­за­ме­не би­ле­те школь­ни­ку попадет­ся во­прос по круглым червям.

Решение: Ве­ро­ят­ность того, что в слу­чай­но вы­бран­ном на эк­за­ме­не би­ле­те школь­ни­ку до­ста­нет­ся во­прос по круглым червям, равна

12 / 25 = 0,48

Ответ: 0,48

5. В сред­нем из 2000 са­до­вых на­со­сов, по­сту­пив­ших в про­да­жу, 2 под­те­ка­ют. Най­ди­те ве­ро­ят­ность того, что один слу­чай­но вы­бран­ный для кон­тро­ля насос не под­те­ка­ет.

Решение: в сред­нем из 2000 са­до­вых на­со­сов, по­сту­пив­ших в про­да­жу, 2000 − 2 = 1998 не под­те­ка­ют. Зна­чит, ве­ро­ят­ность того, что один слу­чай­но вы­бран­ный для кон­тро­ля насос не под­те­ка­ет, равна

1998 / 2000 = 999 / 1000 = 0,999

Ответ: 0,999

6. В слу­чай­ном экс­пе­ри­мен­те сим­мет­рич­ную мо­не­ту бро­са­ют два­жды. Най­ди­те ве­ро­ят­ность того, что решка вы­па­дет ровно один раз.

Решение: Рав­но­воз­мож­ны 4 ис­хо­да экс­пе­ри­мен­та: орел-орел, орел-решка, решка-орел, решка-решка. Решка вы­па­да­ет ровно один раз в двух слу­ча­ях: орел-решка и решка-орел. По­это­му ве­ро­ят­ность того, что решка вы­па­дет ровно 1 раз, равна

2 / 4 = 1 / 2 =0,5

Ответ: 0,5

7. Монету бросают трижды. Найдите вероятность того, что первые два броска окончатся одинаково.

Решение: Пусть орёл - О, решка - Р. Возможные варианты выпадения монеты: ООО, ООР, ОРО, РОО, ОРР, РОР, РРО, РРР. Всего вариантов - 8. Из них благоприятных вариантов - 4 (первый, второй, седьмой и восьмой). Поэтому, вероятность того, что первые два броска окончатся одинаково равна

4 / 8 = 1 / 2 = 0,5

Ответ: 0,5

8. В среднем на 150 карманных фонариков приходится три неисправных. Найдите вероятность купить работающий фонарик.

Решение: в среднем на 150 карманных фонариков приходится 150 - 3 = 147 работающих фонариков.  Вероятность купить рабочий фонарик равна

147 / 150 = 49 / 50 = 98 / 100 = 0,98

Ответ: 0,98

9. В среднем из каждых 50 поступивших в продажу аккумуляторов 48 аккумуляторов заряжены. Найдите вероятность того, что купленный аккумулятор не заряжен.

Решение: в среднем из каждых 50 поступивших в продажу аккумуляторов 50 - 48 = 2 аккумулятора не заряжены. Вероятность того, что купленный аккумулятор будет не заряжен, равен

2 / 50 = 1 / 25 = 0,04

Ответ: 0,04

10. Марина и Дина бросают кубик по одному разу. Выигрывает та девочка, у которой выпадет больше очков. Первой кубик бросила Марина, у нее выпало 3 очка. Найдите вероятность того, что Дина выиграет.

Решение: Чтобы выиграла Дина, у неё должно выпасть число большее 3-х, т.е. 4; 5; 6.
Благоприятных  возможностей - 3.
Всего возможностей - 6 (1; 2; 3; 4; 5; 6).
Вероятность благоприятного исхода - это 3 / 6 = 0,5 

Ответ: 0,5

11. В некоторой местности утро в июле может быть либо ясным, либо пасмурным. Наблюдения показали:
Если июльское утро ясное, то вероятность дождя в этот день 0,1.
Если июльское утро пасмурное, то вероятность дождя в течение дня равна 0,5.
Вероятность того, что утро в июле будет пасмурным равна 0,2.
Найдите вероятность того, что в случайно взятый июльский день дождя не будет.

Решение: 1) вероятность, что утро будет ясное: 1 - 0,2 = 0,8
2) вероятность, что при ясном утро, дождя не будет: 1 - 0,1 = 0,9
3) найдём вероятность, что в случайно взятый июльский день утро будет ясное и дождя не будет: 0,8 · 0,9 = 0,72
4) вероятность, что утро будет пасмурным: 0,2
5) вероятность, что при пасмурном утро, дождя не будет: 1 - 0,5 = 0,5
6) найдём вероятность, что в случайно взятый июльский день утро будет пасмурным и дождя не будет: 0,2 · 0,5 = 0,1
7) найдём вероятность, что в случайно взятый июльский день дождя не будет: 0,72 + 0,1 = 0,82

Ответ: 0,82

12. В каждой пятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Галя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Галя не найдёт приз в своей банке.

Решение: Так как, согласно условиям в каждой пятой банке кофе есть приз,
то в остальных 4-х приза нет.
Тогда, вероятность того, что Галя не найдёт приз в своей банке равна 

4 / 5 = 0,8

Ответ: 0,8

13. Перед началом матча по футболу судья бросает монету, чтобы определить, какая из команд будет первая владеть мячом. Команда "Белые" по очереди играет с командами "Красные", "Синие", "Зеленые". Найдите вероятность того, что ровно в двух матчах из трёх право первой владеть мячом получит команда "Белые".

Решение: Составляем список всех возможных исходов в этих трёх играх с "Красными" (К), "Синими" (С) и "Зелеными" (З).
П - первая владеет мячом, Н - нет.

ППП
ППН
ПНП
НПП
ПНН
НПН
ННП
ННН

и смотрим, в сколько из них содержится ровно 2 раза П, т.е. ровно в двух матчах команда "Белые" будет первой вдладеть мячом.
Таких вариантов 3, а всего вариантов - 8. Тогда искомая вероятность равна

3 / 8 = 0,375

Ответ: 0,375

14. Двое играют в кости - они по разу бросают игральный кубик. Выигрывает тот, у кого больше очков. Если выпадает поровну, то ничья. Первый бросил кубик, и у него выпало 4 очка. Найти вероятность того, что он выиграет.

Решение: первый выиграет, если при броске второго выпадет на кубике число меньшее 4, то есть либо 1, либо 2, либо 3 (всего 3 благопритяных случая).
Количество возможных событий 6 (выпадет либо 1, либо 2, либо 3, либо 4, либо 5, либо 6).
Поэтому вероятность победы первого игрока равна

3 / 6 = 0,5

Ответ: 0,5

15. В сред­нем из 1800 са­до­вых на­со­сов, по­сту­пив­ших в про­да­жу, 18 под­те­ка­ют. Най­ди­те ве­ро­ят­ность того, что один слу­чай­но вы­бран­ный для кон­тро­ля насос не под­те­ка­ет.

Решение: в сред­нем из 1800 са­до­вых на­со­сов, по­сту­пив­ших в про­да­жу, 1800 − 18 = 1782 не под­те­ка­ют. Зна­чит, ве­ро­ят­ность того, что один слу­чай­но вы­бран­ный для кон­тро­ля насос не под­те­ка­ет, равна

1782 / 1800 = 0,99

Ответ: 0,99

16. В тор­го­вом цен­тре два оди­на­ко­вых ав­то­ма­та про­да­ют чай. Ве­ро­ят­ность того, что к концу дня в ав­то­ма­те за­кон­чит­ся чай, равна 0,4. Ве­ро­ят­ность того, что чай за­кон­чит­ся в обоих ав­то­ма­тах, равна 0,2. Най­ди­те ве­ро­ят­ность того, что к концу дня чай оста­нет­ся в обоих ав­то­ма­тах.

Решение: Рас­смот­рим со­бы­тия

А = чай за­кон­чит­ся в пер­вом ав­то­ма­те,
В = чай за­кон­чит­ся во вто­ром ав­то­ма­те.

Тогда

A·B = чай за­кон­чит­ся в обоих ав­то­ма­тах,
A + B = чай за­кон­чит­ся хотя бы в одном ав­то­ма­те.

По усло­вию        P(A) = P(B) = 0,4;        P(A·B) = 0,2.

Со­бы­тия A и B сов­мест­ные, ве­ро­ят­ность суммы двух сов­мест­ных со­бы­тий равна сумме ве­ро­ят­но­стей этих со­бы­тий, умень­шен­ной на ве­ро­ят­ность их про­из­ве­де­ния:

P(A + B) = P(A) + P(B) − P(A·B) = 0,4 + 0,4 − 0,2 = 0,6

Сле­до­ва­тель­но, ве­ро­ят­ность про­ти­во­по­лож­но­го со­бы­тия, со­сто­я­ще­го в том, что чай оста­нет­ся в обоих ав­то­ма­тах, равна 1 − 0,6 = 0,4

Ответ: 0,4

17. В сред­нем из 900 са­до­вых на­со­сов, по­сту­пив­ших в про­да­жу, 27 под­те­ка­ют. Най­ди­те ве­ро­ят­ность того, что один слу­чай­но вы­бран­ный для кон­тро­ля насос не под­те­ка­ет.

Решение: в сред­нем из 900 са­до­вых на­со­сов, по­сту­пив­ших в про­да­жу, 900 − 27 = 873 не под­те­ка­ют. Зна­чит, ве­ро­ят­ность того, что один слу­чай­но вы­бран­ный для кон­тро­ля насос не под­те­ка­ет, равна

873 / 900 = 0,97

Ответ: 0,97

18. В каждой двадцать пятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Коля покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Коля не найдёт приз в своей банке.

Решение: Так как, согласно условиям в каждой двадцать пятой банке кофе есть приз,
то в остальных 24-х приза нет.
Тогда, вероятность того, что Коля не найдёт приз в своей банке равна 

24 / 25 = 0,96

Ответ: 0,96

19. Конкурс исполнителей проводится в 3 дня. Всего заявлено 80 выступлений - по одному от каждой страны. В первый день запланировано 20 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?

Решение: всего 80 выступлений
80 - 20 = 60 выступлений осталось на 2 дня
60 : 2 = 30 выступлений в каждые остальные 2 дня.

Тогда, всего - 80
30 - в 3 день

Р = 30 / 80 = 3 / 8 = 0,375 

Ответ: 0,375

20. Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 56 шашистов, среди которых 12 участников из России, в том числе Валерий Стремянкин. Найдите вероятность того, что в первом туре Валерий Стремянкин будет играть с каким-либо шашистом из России?

Решение: В пер­вом туре Валерий Стремянников может сыг­рать с  56 - 1 = 55 шашистом, из ко­то­рых 12 - 1 = 11 из Рос­сии. Зна­чит ве­ро­ят­ность того, что в пер­вом туре Валерий Стремянкин будет иг­рать с каким-либо шашистом из Рос­сии, равна 

11 / 55 = 0,2 

Ответ: 0,2

21. В ма­га­зи­не стоят два платёжных ав­то­ма­та. Каж­дый из них может быть не­ис­пра­вен с ве­ро­ят­но­стью 0,06 не­за­ви­си­мо от дру­го­го ав­то­ма­та. Най­ди­те ве­ро­ят­ность того, что хотя бы один ав­то­мат ис­пра­вен. 

Решение: Най­дем ве­ро­ят­ность того, что не­ис­прав­ны оба ав­то­ма­та.
Эти со­бы­тия не­за­ви­си­мые, ве­ро­ят­ность их про­из­ве­де­ния равна про­из­ве­де­нию ве­ро­ят­но­стей этих со­бы­тий: 

0,06 · 0,06 = 0,0036

Со­бы­тие, со­сто­я­щее в том, что ис­пра­вен хотя бы один ав­то­мат, про­ти­во­по­лож­ное.
Сле­до­ва­тель­но, его ве­ро­ят­ность равна 

1 − 0,0036 = 0,9964

Ответ: 0,9964

22. В сборнике билетов по химии всего 15 билетов, в 6 из них встречается вопрос по теме "Кислоты". Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме "Кислоты". 

Решение: Вероятность, того что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме "Кислоты", равна 

Ответ: 0,4

23. В сборнике билетов по философии всего 25 билетов, в 15 из них встречается вопрос о философии Пифагора. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос о философии Пифагора. 

Решение: Вероятность, того что в случайно выбранном на экзамене билете школьнику достанется вопрос о философии Пифагора, равна 

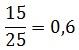
Ответ: 0,6

24. В слу­чай­ном экс­пе­ри­мен­те сим­мет­рич­ную мо­не­ту бро­са­ют четыре­жды. Най­ди­те ве­ро­ят­ность того, что орёл вы­па­дет ровно три раза.

Решение: Обозначим выпадение орла через О, выпадение решки через Р.

Тогда возможны следующие варианты: ОООО, ОООР, ООРО, ОРОО, РООО, ООРР, ОРОР, РООР, ОРРО, РОРО, РРОО, ОРРР, РОРР, РРОР, РРРО, РРРР.

Всего возможных вариантов: 16.

Из них орёл выпадет ровно три раза в 4 вариантах (выделены полужирным начертанием).

По­это­му ве­ро­ят­ность того, что орёл вы­па­дет ровно 3 раза, равна

4 / 16 = 1 / 4 =0,25

Ответ: 0,25

25. В слу­чай­ном экс­пе­ри­мен­те сим­мет­рич­ную мо­не­ту бро­са­ют трижды. Най­ди­те ве­ро­ят­ность того, что решка вы­па­дет все три раза.

Решение: Обозначим выпадение орла через О, выпадение решки через Р.

Тогда возможны следующие варианты: ООО, ООР, ОРО, РОО, ОРР, РОР, РРО, РРР.

Всего возможных вариантов: 8.

Из них решка выпадет все три раза в одном варианте (выделен полужирным начертанием).

По­это­му ве­ро­ят­ность того, что решка вы­па­дет все 3 раза, равна

1 / 8 = 0,125

Ответ: 0,125

26. Вероятность того, что новый персональный компьютер прослужит больше года, равна 0,98. Вероятность того, что он прослужит больше двух лет, равна 0,84. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.

Решение: 1) вероятность того, что он прослужит меньше двух лет 1 – 0,84 = 0,16
2) вероятность того, что он прослужит больше года, дана в условии 0,98
3) значит вероятность того, что он сломается за первый год равна 1 – 0,98 = 0,02
4) вероятность того, что он прослужит меньше двух лет, но больше года 0,16 – 0,02 = 0,14

Ответ: 0,14

27. В группе туристов 5 человек, в том числе турист Д. С помощью жребия они выбирают трёх человек, которые должны идти в село за продуктами. Какова вероятность того, что туристу Д. выпадет по жребию идти в село?

Решение: число всех исходов - 5, благоприятных - 3. Тогда, вероятность будет равна 3/5 = 0,6

Ответ: 0,6

28. Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,3. На столе лежат 10 револьверов, из них только 2 пристрелянные.Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.

Решение: Вероятность того, что пистолет пристрелянный равна 2/10 = 0,2, что  не пристрелянный 8/10 = 0,8
Вероятность того, что попадется пристрелянный и Джон попадет, равна 0,2 · 0,9 = 0,18
Вероятность того, что попадется непристрелянный и Джон попадет, равна 0,8 · 0,3 = 0,24

Вероятность попасть:  0,18 + 0,24 = 0,42
Вероятность промаха: Р = 1 - 0,42 = 0,58

Ответ: 0,58

29. В некотором городе из 2000 появившихся на свет младенцев 990 девочек. Найдите частоту рождения мальчиков в этом городе. Результат округлите до тысячных.

Решение: 1. Если на 2000 рожденных младенцев приходится 990 девочек, то:
2000 - 990 = 1010 мальчиков приходится на 2000 рожденных детей.

2. Частота = 1010 / 2000 = 505 / 1000 = 0,505

Ответ: 0,505

30. В группе туристов 8 человек, в том числе турист A. С помощью жребия они выбирают двух человек, которые должны идти в село за продуктами. Какова вероятность того, что туристу А. выпадет по жребию идти в село?

Решение: число всех исходов - 8, благоприятных - 2. Тогда, вероятность будет равна 2/8 = 1/4 = 0,25

Ответ: 0,25

31. В группе туристов 10 человек, в том числе турист A. С помощью жребия они выбирают двух человек, которые должны идти в село за продуктами. Какова вероятность того, что туристу А. выпадет по жребию идти в село?

Решение: число всех исходов - 10, благоприятных - 2. Тогда, вероятность будет равна 2/10 = 1/5 = 0,2

Ответ: 0,2

32. Павел Иванович совершает прогулку из точки A по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Найдите вероятность того, что Павел Иванович попадёт в точку G.

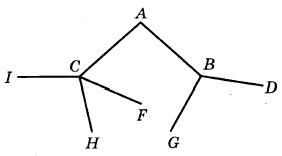
Решение: Чтобы попасть в точку G, Павел Иванович должен будет сначала попасть в точку B (так как если он сначала попадет в точку C, то по условию задачи вернуться обратно в точку A он не сможет).
Вероятность того, что Павел Иванович попадёт в точку B равна 1 / 2 (так как из точки A выходят 2 дорожки).
Вероятность того, что Павел Иванович из точки B попадёт в точку G равна 1 / 2 (так как из точки B выходят 2 дорожки). 

Тогда, вероятность того, что Павел Иванович из точки A попадёт в точку G равна произведению вероятностей: 

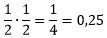
Ответ: 0,25

33. По отзывам покупателей Игорь Игоревич оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,94. Вероятность того, что этот товар доставят из магазина Б, равна 0,8. Игорь Игоревич заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.

Решение: Вероятность того, что магазин А не доставит товар равна 1 - 0,94 = 0,06.
Вероятность того, что магазин Б не доставит товар равна 1 - 0,8 = 0,2.
Так как, эти событи независимы друг от друга, то вероятность того, что оба магазина не доставят товар, равна произведению вероятностей этих событий: 0,06 · 0,2 = 0,012

Ответ: 0,012

34. В сборнике билетов по истории всего 50 билетов, в 13 из них встречается вопрос о Великой Отечественной войне. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос о Великой Отечественной войне.

Решение: вероятность того, что в случайно выбранном билете достанется вопрос о Великой Отечественной войне равна: 

13 / 50 =  0,26

Ответ: 0,26

35. В сборнике билетов по математике всего 20 билетов, в 5 из них встречается вопрос по теории вероятностей. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теории вероятностей.

Решение: вероятность того, что в случайно выбранном билете достанется вопрос по теории вероятностей равна: 

5 / 20 = 1 / 4 = 0,25

Ответ: 0,25

36. Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,5. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,32. Шахматисты А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.

Решение: Возможность выиграть первую и вторую партию не зависят друг от друга. Вероятность произведения независимых событий равна произведению их вероятностей: 0,5 · 0,32 = 0,16

Ответ: 0,16

37. Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,5. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.

Решение: Возможность выиграть первую и вторую партию не зависят друг от друга. Вероятность произведения независимых событий равна произведению их вероятностей: 0,5 · 0,3 = 0,15

Ответ: 0,15

1. В классе 7 мальчиков и 14 девочек. 1 сентября случайным образом определяют двух дежурных на 2 сентября, которые должны приготовить класс к занятиям. Найдите вероятность того, что будут дежурить два мальчика. 

2. В фирме такси в дан­ный мо­мент сво­бод­но 10 машин: 5 чер­ных, 1 жел­тая и 4 зе­ле­ных. По вы­зо­ву вы­еха­ла одна из машин, слу­чай­но ока­зав­ша­я­ся ближе всего к за­каз­чи­ку. Най­ди­те ве­ро­ят­ность того, что к нему при­е­дет жёлтое такси.

3. В слу­чай­ном экс­пе­ри­мен­те бро­са­ют две иг­раль­ные кости. Най­ди­те ве­ро­ят­ность того, что в сумме вы­па­дет 7 очков. Ре­зуль­тат округ­ли­те до сотых.

4. В сбор­ни­ке би­ле­тов по био­ло­гии всего 25 би­ле­тов, в 12 из них встре­ча­ет­ся во­прос по круглым червям. Най­ди­те ве­ро­ят­ность того, что в слу­чай­но вы­бран­ном на эк­за­ме­не би­ле­те школь­ни­ку попадет­ся во­прос по круглым червям.

5. В сред­нем из 2000 са­до­вых на­со­сов, по­сту­пив­ших в про­да­жу, 2 под­те­ка­ют. Най­ди­те ве­ро­ят­ность того, что один слу­чай­но вы­бран­ный для кон­тро­ля насос не под­те­ка­ет.

6. В слу­чай­ном экс­пе­ри­мен­те сим­мет­рич­ную мо­не­ту бро­са­ют два­жды. Най­ди­те ве­ро­ят­ность того, что решка вы­па­дет ровно один раз.

7. Монету бросают трижды. Найдите вероятность того, что первые два броска окончатся одинаково.

8. В среднем на 150 карманных фонариков приходится три неисправных. Найдите вероятность купить работающий фонарик.

9. В среднем из каждых 50 поступивших в продажу аккумуляторов 48 аккумуляторов заряжены. Найдите вероятность того, что купленный аккумулятор не заряжен.

10. Марина и Дина бросают кубик по одному разу. Выигрывает та девочка, у которой выпадет больше очков. Первой кубик бросила Марина, у нее выпало 3 очка. Найдите вероятность того, что Дина выиграет.

11. В некоторой местности утро в июле может быть либо ясным, либо пасмурным. Наблюдения показали:
Если июльское утро ясное, то вероятность дождя в этот день 0,1.
Если июльское утро пасмурное, то вероятность дождя в течение дня равна 0,5.
Вероятность того, что утро в июле будет пасмурным равна 0,2.
Найдите вероятность того, что в случайно взятый июльский день дождя не будет.

12. В каждой пятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Галя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Галя не найдёт приз в своей банке.

13. Перед началом матча по футболу судья бросает монету, чтобы определить, какая из команд будет первая владеть мячом. Команда "Белые" по очереди играет с командами "Красные", "Синие", "Зеленые". Найдите вероятность того, что ровно в двух матчах из трёх право первой владеть мячом получит команда "Белые".

14. Двое играют в кости - они по разу бросают игральный кубик. Выигрывает тот, у кого больше очков. Если выпадает поровну, то ничья. Первый бросил кубик, и у него выпало 4 очка. Найти вероятность того, что он выиграет.

15. В сред­нем из 1800 са­до­вых на­со­сов, по­сту­пив­ших в про­да­жу, 18 под­те­ка­ют. Най­ди­те ве­ро­ят­ность того, что один слу­чай­но вы­бран­ный для кон­тро­ля насос не под­те­ка­ет.

16. В тор­го­вом цен­тре два оди­на­ко­вых ав­то­ма­та про­да­ют чай. Ве­ро­ят­ность того, что к концу дня в ав­то­ма­те за­кон­чит­ся чай, равна 0,4. Ве­ро­ят­ность того, что чай за­кон­чит­ся в обоих ав­то­ма­тах, равна 0,2. Най­ди­те ве­ро­ят­ность того, что к концу дня чай оста­нет­ся в обоих ав­то­ма­тах.

17. В сред­нем из 900 са­до­вых на­со­сов, по­сту­пив­ших в про­да­жу, 27 под­те­ка­ют. Най­ди­те ве­ро­ят­ность того, что один слу­чай­но вы­бран­ный для кон­тро­ля насос не под­те­ка­ет.

18. В каждой двадцать пятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Коля покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Коля не найдёт приз в своей банке.

19. Конкурс исполнителей проводится в 3 дня. Всего заявлено 80 выступлений - по одному от каждой страны. В первый день запланировано 20 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?

20. Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 56 шашистов, среди которых 12 участников из России, в том числе Валерий Стремянкин. Найдите вероятность того, что в первом туре Валерий Стремянкин будет играть с каким-либо шашистом из России?

21. В ма­га­зи­не стоят два платёжных ав­то­ма­та. Каж­дый из них может быть не­ис­пра­вен с ве­ро­ят­но­стью 0,06 не­за­ви­си­мо от дру­го­го ав­то­ма­та. Най­ди­те ве­ро­ят­ность того, что хотя бы один ав­то­мат ис­пра­вен. 

22. В сборнике билетов по химии всего 15 билетов, в 6 из них встречается вопрос по теме "Кислоты". Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме "Кислоты". 

23. В сборнике билетов по философии всего 25 билетов, в 15 из них встречается вопрос о философии Пифагора. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос о философии Пифагора. 

24. В слу­чай­ном экс­пе­ри­мен­те сим­мет­рич­ную мо­не­ту бро­са­ют четыре­жды. Най­ди­те ве­ро­ят­ность того, что орёл вы­па­дет ровно три раза.

25. В слу­чай­ном экс­пе­ри­мен­те сим­мет­рич­ную мо­не­ту бро­са­ют трижды. Най­ди­те ве­ро­ят­ность того, что решка вы­па­дет все три раза.

26. Вероятность того, что новый персональный компьютер прослужит больше года, равна 0,98. Вероятность того, что он прослужит больше двух лет, равна 0,84. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.

27. В группе туристов 5 человек, в том числе турист Д. С помощью жребия они выбирают трёх человек, которые должны идти в село за продуктами. Какова вероятность того, что туристу Д. выпадет по жребию идти в село?

28. Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,3. На столе лежат 10 револьверов, из них только 2 пристрелянные.Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.

29. В некотором городе из 2000 появившихся на свет младенцев 990 девочек. Найдите частоту рождения мальчиков в этом городе. Результат округлите до тысячных.

30. В группе туристов 8 человек, в том числе турист A. С помощью жребия они выбирают двух человек, которые должны идти в село за продуктами. Какова вероятность того, что туристу А. выпадет по жребию идти в село?

31. В группе туристов 10 человек, в том числе турист A. С помощью жребия они выбирают двух человек, которые должны идти в село за продуктами. Какова вероятность того, что туристу А. выпадет по жребию идти в село?

32. Павел Иванович совершает прогулку из точки A по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Найдите вероятность того, что Павел Иванович попадёт в точку G.

33. По отзывам покупателей Игорь Игоревич оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,94. Вероятность того, что этот товар доставят из магазина Б, равна 0,8. Игорь Игоревич заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.

34. В сборнике билетов по истории всего 50 билетов, в 13 из них встречается вопрос о Великой Отечественной войне. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос о Великой Отечественной войне.

35. В сборнике билетов по математике всего 20 билетов, в 5 из них встречается вопрос по теории вероятностей. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теории вероятностей.

36. Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,5. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,32. Шахматисты А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.

37. Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,5. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.