Урок 77 Преобразование целого выражения в многочлен
Цели: ввести понятие целого выражения; формировать умение преобразовывать целые выражения.
Ход урока
I. Устная работа.
Преобразуйте в многочлен.
а) ![]() x (2x2 – 4); в) (x + 4)2; б) (x + 3) (x – 3);
x (2x2 – 4); в) (x + 4)2; б) (x + 3) (x – 3);
г)  ; д) (a – 1) (a2 + a + 1); ж) (x – 3) (y – 2);
; д) (a – 1) (a2 + a + 1); ж) (x – 3) (y – 2);
е)  ; з) (–1 – 2n)2.
; з) (–1 – 2n)2.
II. Объяснение нового материала.
Объяснение проводить согласно пункту 37 учебника в несколько этапов.
1. Введение понятия целого выражения.
Сначала необходимо напомнить учащимся о том, что такое математическое выражение, а затем дать определение целого выражения. Сделать вывод: математическое выражение может быть целым или нецелым.
После этого привести примеры и выполнить № 918.
2. Целое выражение и многочлен.
На основе изученного учащиеся сами смогут сделать вывод, что любой многочлен является целым выражением. После этого следует задать им вопрос: любое ли целое выражение является многочленом?
Делаются соответствующие выводы, приводятся примеры, показывающие, как целое выражение представляется в виде многочлена.
3. Преобразование целых выражений.
Сообщить учащимся, что преобразование целых выражений является одним из основных действий в математике. Чтобы выполнять такие преобразования, нужно уметь следующее:
– выполнять умножение одночлена на многочлен и многочлена на многочлен;
– приводить подобные слагаемые;
– знать формулы сокращенного умножения.
Далее привести пример 1 из учебника.
III. Формирование умений и навыков.
Для преобразования целых выражений учащиеся выполняют действия, которые уже должны быть у них отработаны в процессе изучения предыдущих тем. По сути, задания, предложенные в учебнике, служат для обобщения и систематизации знаний и умений учащихся.
1. Упростите выражение.
а) (4a – b) (a – 6b) + a (25b – 3a);
б) 2c (5c – 3) – (c – 2) (c – 4);
в) (y – 3) (5 – y) – (4 – y) (y + 6).
2. Преобразуйте в многочлен.
а) ![]() в)
в) ![]()
б) 4b (3b + 6) – (3b – 5) (5 + 3b); г) ![]()
3. Найдите значение выражения.
а) ![]() при х = –3,5;
при х = –3,5;
б) ![]() при a = 1
при a = 1![]() , b = 0,7.
, b = 0,7.
4. Упростите выражение.
а) ![]()
б) ![]()
Решение:
а) Можно выполнять возведение в квадрат и раскрывать скобки, но это будет нерационально. Заметим, что данное выражение является полным квадратом.
![]() (4a3 – 1))2 =
(4a3 – 1))2 =
= (4a3 + 5 – 4a3 + 1)2 = 62 = 36.
б) ![]()
= 4x3 – 4x2 + x – 2x3 – 2 = 2x3 – 4x2 + x – 2.
IV. Итоги урока.
– Какие математические выражения называются целыми?
– Приведите примеры целых выражений и выражений, которые не являются целыми.
– Являются ли многочлены целыми выражениями?
– Любое ли целое выражение можно представить в виде многочлена?
Домашнее задание: № 920, № 921, № 922.
Урок 78 Преобразование целого выражения в многочлен
Цели: продолжить формирование умения преобразовывать целые выражения; проверить уровень усвоения материала.
Ход урока
I. Устная работа.
1. Какие из следующих выражений являются целыми:
а) 3x2 – 2a; в) ![]() ; д)
; д)  – 4;
– 4;
б) ![]() ; г)
; г) ![]() ; е)
; е)  ?
?
2. Преобразуйте в многочлен.
а) ![]() в) (x – 5) (y – 2);
в) (x – 5) (y – 2);
б) (–x – 4)2; г)  .
.
II. Формирование умений и навыков.
1. № 923. 2. № 925. 3. № 927 (а).
4*. № 999 (а).
Решение:
а) ![]()
![]()
![]() a4 – 4a2 + 11 –
a4 – 4a2 + 11 –
– a4 – a3 + 2,5a2 – 1,5a + 6 = –a3 – 1,5a2 – 1,5a + 17.
III. Проверочная работа.
Вариант 1
1. Преобразуйте в многочлен.
а) (c + 2) (c – 3) – (c + 1) (c + 3); б) ![]()
в) ![]()
2. Найдите значение выражения
(3a + b)2 – (3a – b)2 при a = 3![]() , b = –0,3.
, b = –0,3.
3. Упростите выражение 8 (5y + 3)2 + 9 (3y – 1)2.
Вариант 2
1. Преобразуйте в многочлен.
а) (a – 5) (a + 1) – (a – 6) (a – 1); б) (a – 4) (a + 4) – 2a (3 – a);
в) (p + 3) (p – 11) + (p + 6)2.
2. Найдите значение выражения
(4x – y)2 – (4x + y)2 при x = 1![]() , y = –0,2.
, y = –0,2.
3. Упростите выражение (2x – 5)2 – 2 (7x – 1)2.
IV. Итоги урока.
Домашнее задание: № 924; № 926; № 928 (а); № 929 (а).
Урок 79 Преобразование целого выражения в многочлен.
Цели: 1) Закрепить навыки преобразования целых выражений.
2) Воспитывать у детей потребности в сохранении и укреплении своего здоровья.
3) Развивать познавательный интерес учащихся, расширять их кругозор, приобщать к творчеству
Тип урока: закрепление изученного материала, урок решения задач.
Оборудование: компьютер (презентация 4), карточки для математического лото, тестовые задания.
Ход урока
Учитель: Сегодня у нас необычный урок повторения темы «Преобразование целого выражения в многочлен», урок здоровья. Я хочу начать урок словами великого мыслителя:
«ЕДИНСТВЕННАЯ КРАСОТА, КОТОРУЮ Я ЗНАЮ, - ЭТО ЗДОРОВЬЕ» ГЕЙНЕ
«Здоровье – сумма слагаемых и произведение сомножителей, главным из которых является элементы образа жизни: его благополучие, физические резервы, образ жизни»
Человек – высшее творение природы. Но для того чтобы наслаждаться ее сокровищами, он должен отвечать, по крайней мере, одному требованию: быть здоровым. Это аксиома, про которую мы в текучке и суете дней, к сожалению, забываем.. За здоровье надо активно бороться. Для этого надо овладеть элементарными знаниями, а также использовать накопленный опыт, которые помогли бы молодым людям сохранять здоровье., Можно приводить много высказываний великих ученых о здоровье, о приобщении к здоровому образу жизни.
II. Устная работа
«Никто не должен переступать меры ни в пище, ни в питании» - сказал великий математик. Чьи это слова, узнаем, выполнив преобразования выражений (учащиеся читают выражения и выбирают вариант ответа ):
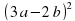

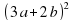
9a – 6b
 - 24ab+
- 24ab+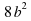
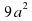 -
- 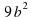
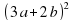 - 12ab
- 12ab
Ответы:
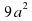 - 12ab +
- 12ab +  (П)
(П)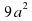 -
-  (И)
(И)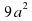 + 12ab +
+ 12ab +  (Ф)
(Ф) (A)
(A) (Г)
(Г) (O)
(O)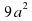 +
+  (P) ПИФАГОР
(P) ПИФАГОР
Доклад – презентация «Пифагор».презентация. Выступает ученик
Пифагор – древнегреческий ученый – математик. Родился Пифагор где-то между 600 и 590 гг. до Рождества Христова и жил около ста лет.
“Пифагор был олицетворением величия и силы, и в его присутствии все чувствовали себя смирными и робкими. По мере того как он становился пожилым, его физические силы отнюдь не убывали, и, когда он достиг столетия, он был полон жизни. Влияние этой великой души на окружающих ее людей было столь велико, что похвала Пифагора наполняла его учеников восторгом…” (Из книги “История прорицаний”)
Его учение, система, которая преподавалась в Пифагорейской школе, является синтезом тех знаний, которые он получил на протяжении своей удивительной. наполненной событиями жизни.
Пифагор обучал своих учеников методам развития тела, моральных и душевных качеств. В Золотых стихах Пифагор описал самые главные моральные правила, суровое выполнение которых приводит души ошибающихся к идеалу . Вот несколько из них:
| ● | Не пренебрегай здоровьем своего тела. Давай ему своевременно пищу, питье и упражнения, в которых оно нуждается. |
| ● | Приучайся жить просто. |
| ● | Делай только то, что в будущем не огорчит тебя. |
| ● | Никогда не делай того, что не знаешь. Но учись всему, что нужно знать, и тогда будешь вести спокойную жизнь. |
| ● | Не пренебрегай здоровьем своего тела. Давай ему своевременно пищу, питье и упражнения, в которых оно нуждается. |
| ● | Не затворяй глаз, когда хочешь спать, не рассмотрев все свои поступки за прошедший день. |
Согласитесь, эти правила сохранили свою актуальность и в наши дни
Пифагор ставил себе задачу совершенствование человечества. Его ученики вставали рано при первых лучах солнца и торжественно с песнями отправлялись навстречу светилу. Философ сообщал ученикам сведения о важнейших предметах человеческого знания, в частности математики.
Простой завтрак, состоящий из хлеба с медом и воды следовал, за утренними телесными упражнениями и играми; дружеский разговор, беседы, наполняли остальные часы дня. Вечер посвящался купанию, ужину, пению и музыке. Такой образ жизни располагал приверженцев Пифагора к добру, исполнял невозмутимым спокойствием. Пифагор изучал количественную сторону мира. Он говорил, что можно узнать судьбу человека, зная его дату рождения. Все четные числа Пифагор относил к женским, нечетные к мужским. Пифагор считал, что число 1 – сущность всех вещей, 2 – женское начало, 3 – мужское, 4 – совершенное число, 5 - символизирует цвет, 6 - холод, 7 - ум, здоровье и свет, 8 - любовь и дружбу, 9 - постоянность.
Математический фокус
Пронумеруем дни недели 1 – понедельник и т.д. Задумайте день недели, умножьте на 2, прибавьте к произведению 5, умножьте сумму на 5, допишите справа нуль и назовите результат. (Ведущий из результата вычитает 250. Цифра сотен дает номер задуманного дня). В чем секрет этого фокуса? (2а+5)*5*10=100а+250-250=100а
Физминутка.
С гимнастикой дружи, всегда веселым будь,
И проживешь сто лет, а может быть, и боле.
Микстуры, порошки – к здоровью ложный путь.
Природою лечись – в саду и в чистом поле.
Решение задач
Поставить вместо пропусков выражения или знаки так, чтобы получилось тождество.
а) (х … y)2 = х2 + 2хy + …
б) (5х – … )(5х + 3) = … – 9
в) (х – 2)( х2 + … + …) = х3 …8
г) (… + …)2 = 36 х2 + 12хy + …
д) (х2 – … )( х2 + …) = … – y2п
е) (… – 5)(… – … + …) = х3 – 125
№2
Известно, что х2 + 2хy + y2 = 9, найдите:
а) (х + y)2 =
б) (х + y)2 – 5 =
в) (2х + 2y)2 =
Самостоятельная работа
Учащиеся выполняют тестовые задания (приложение 1)
Итог урока.
Урок заканчивается словами Авиценны:
В ком воля есть и сильный дух,
Тот победит любой недуг, -
Болезнь отступит перед гордым,
Перед бесстрашным, непокорным.
Известно, что сильная воля нужна каждому человеку, она помогает выстоять при любых обстоятельствах – при решении сложной задачи, при занятиях спортом, при воспитании своего характера, при изживании отрицательных качеств.
Задание на дом: Карточки с домашним заданием учащиеся выполняют в виде проекта.
Он состоит из пяти заданий. Три в виде теста, т.е., учащиеся придумывают пример (берут из учебника и т.д.) на любую из формул сокращенного умножения, преобразования целого выражения в многочлен и к каждому из них четыре варианта ответов , 4 и 5 – творческие (более сложные задания без ответов). Ко всем этим заданиям прилагается листок с правильными ответами. После проверки и корректировки учителем данного материала, учащиеся его дорабатывают и сдают учителю на повторную проверку. Получается индивидуальная карточка для каждого учащегося выполненная кем-то из его одноклассников.
Приложение 1
ТЕСТ
Вариант 1
В примерах 1-5 раскройте скобки: 1. (х + 2у) 2
А. х2 + 4ху + Ау2 В. x2 + 4у2.
Б. x2 + 4ху + 2y2. Г. x2 + 2ху + 2x2.
2. (2а - З)2.
А. 4а2 -6а + 9. В. 2а2 - 12а+ 9.
Б. 4а2-12а+ 9. Г. 4а2-9.
3. (Зх - 5у2) (Зх + 5у2).
А. 9х2 - 25у2. В. 9x2 + 25у2
Б. 9х2 + 25y4. Г. 9x2 - 25у4
4. (а + 2) (а2 - 2а + 4).
А. а3+16. В. а3 + 2а2 + 8.
Б. а3-8. Г. а3+ 8.
5. (х + 1) (х2 - х +1).
А. x3 + х2-1. Б. x3-1. В. х3-х2-1. Г. x3 + 1.
6. Даны два равенства:
(2а – 3b2)2 = 4а2 - 6аb2+ 9b4;
(х + Зy)2 = x2 + 9y2 + 6xy.
Какое из них верно (да), а какое неверно (нет)?
А. Да, да. Б. Да, нет. В. Нет, да. Г, Нет, пот.
7. Не решая пример, скажите, (да) или (нет)следующее задание:
Разделите многочлен Зх2у - 9ху2 на одночлен Зх2у.
Разделите многочлен Зхуz – 9xy2z на одночлсш 3y.
А. Да, да. Б. Да, нет. В. Нет, да, Г, Нет, нет.
Вариант 2
В примерах 1-5 раскройте скобки: 1. (За + Ь)2.
А. 9а2 + b2 В. 9а2 + 3ab + b2.
Б. 9а2 + 6аb + b2. Г. За2 + 6ab + b2.
2. (За - 2)2.
А. 9а2 - 6а + 4. В. 9а2 - 12а + 4.
Б. За2-12а+ 4. Г. 9а2-4.
3. (2х – 3y2) (2х + Зy2).
А. 4х2 - 9у2. В. 4x2 + 9y2.
Б. 4х2 - 9у4. Г. 4х2
4. (а - 2) (а2 + 2а + 4).
А. а3-8. Б. а3+ 8. В. а3-2а2+ 8. Г. а3 - 16.
5. (х + 1) (х2 - х +1).
А. x3 + х2-1. Б. x3-1. В. х3-х2-1. Г. x3 + 1.
6. Даны два равенства:
(Зx2 + 2у)2 == Ау2 + 12х2у + 9x4;
(За - b)2 - 9а2 + b2 - 6аb.
Какое из них верно (дa), a какое неверно (нет)?
А. Да, да. Б. Да, нет. В. Нет, да. Г. Нет, нет.
7. Не решая пример, скажите, (да) или (нет)следующее задание:
Разделите многочлен 4a3b -8a2b на одночлен 2аb2.
Разделите многочлен 5аbс - 10 ab2c3 на одночлен 5a2b.
А. Да, да. Б. Да, нет. В. Нет, да. Г. Нет, нет.
Урок 80 Применение различных способов для разложения
на множители
Цели: повторить известные способы разложения многочлена на множители и закрепить умение их применять.
Ход урока
I. Устная работа.
Разложите многочлен на множители.
а) 5х3 – 10х; г) y2 + 6y + 9; ж) а3 + 1;
б) а2 – 4; д) 4х2 – 4х + 1; з) 49p2 – q4.
в) ![]() – х2; е)
– х2; е) ![]()
III. Формирование умений и навыков.
1. № 934 (а, в, д), № 935.
2. № 937.
3. № 938. 4. № 939 (а, в, д). 5. № 942 (а, в).
IV. Итоги урока.
Домашнее задание: № 934 (б, г, е); № 936; № 939 (б, г, е); № 942
(б, г).
Урок 81 Применение различных способов для разложения
на множители
Цели: закрепить умение раскладывать многочлен на множители; рассмотреть особенности применения способа группировки в сочетании с формулами сокращенного умножения; проверить уровень усвоения материала.
Ход урока
I. Устная работа.
Разложите многочлен на множители.
а) 4a2 – 8a; г) n2 + 8n + 16; ж) х3 – 1;
б) х2 – 100; д) 9х2 – 6х + 1; з) 225a2 – c6.
в) ![]() – a2; е) 25p2 –
– a2; е) 25p2 – ![]() q2;
q2;
II. Формирование умений и навыков.
4. № 1010.
Разобрать пример 3 из учебника и сделать вывод о том, что не всегда члены многочлена группируются по два.
1. № 944. 2. № 946 (а, г).
III. Проверочная работа.
Вариант 1
1. Разложите на множители.
а) 3х2 – 12; в) ax2 + 4ax + 4a;
б) –3a3 + 3ab2; г) –3x2 + 12x – 12.
2. Представьте в виде произведения.
а) б)
3*. Какой многочлен надо записать вместо *, чтобы получившееся равенство было тождеством:
(x + 1) ∙ * = x2 + 3x + 2?
Вариант 2
1. Разложите на множители.
а) 5x2 – 45; в) ax2 – 2axy + ay2;
б) –2ay2 + 2a3; г) –2x2 – 8x – 8.
2. Представьте в виде произведения.
а) б)
3*. Какой многочлен надо записать вместо *, чтобы получившееся равенство было тождеством:
(x – 1) ∙ * = x2 – 4x + 3?
IV. Итоги урока.
– Какие вы знаете способы разложения многочлена на множители?
– В чём состоит каждый из этих способов?
– Как способ группировки применяется в сочетании с формулами сокращенного умножения?
Домашнее задание: № 945; № 947, 1011
Урок 82. Применение различных способов для разложения
на множители
Цели: закрепить умение использовать различные способы разложения многочлена на множители; рассмотреть решение некоторых задач с применением разложения на множители.
Ход урока
I. Устная работа.
Разложите многочлен на множители.
а) 4y5 – 6y8; б) 4900 – а2; в) x2 – ;
г) y2 – 6y + 9; д) 81x2 – ![]() y2; е) 25a2 – 10a + 1;
y2; е) 25a2 – 10a + 1;
ж) у3 + 8; з) 121n2 – m10.
II. Формирование умений и навыков.
На этом уроке следует рассмотреть, как могут быть применены различные способы разложения на множители при решении задач. Можно выделить три направления такого применения:
1) для упрощения вычислений на калькуляторе;
2) для решения уравнений;
3) для доказательства некоторых утверждений.
В соответствии с этим все задания можно разделить на три группы.
1-я группа
Сначала необходимо рассмотреть пример 4 из учебника, показывающий, как можно рационально выполнить вычисления на калькуляторе, если использовать разложение на множители. Для закрепления следует выполнить № 948.
2-я группа
1. № 949. 1. № 951.
Решение:
Разложим данный многочлен на множители:
Получили произведение трёх последовательных целых чисел. Так как числа последовательные, то хотя бы одно из них чётно, то есть кратно 2, а другое кратно 3. Это означает, что всё произведение кратно 6.
2. № 952.
Решение:
Пусть 2п + 1 и 2п + 3 – два последовательных нечётных числа. Найдем разность их квадратов.
(2п + 3)2 – (2п + 1)2 = ((2п + 3) – (2п + 1)) ((2п + 3) + (2п + 1)) =
= (2п + 3 – 2п – 1) (2п + 3 + 2п + 1) = 2 (4п + 4) = 8 (п + 1).
Значит, исходное выражение делится на 8.
III. Итоги урока.
– Какие вы знаете способы разложения на множители?
– Опишите суть каждого способа.
– При решении каких задач пригодится умение раскладывать многочлен на множители?
Домашнее задание: № 950; № 953; № 998 (а); № 1012 (а, г).
Урок 83 Контрольная работа № 8
Вариант 1
1. Упростите выражение.
а) (x – 3) (x – 7) – 2x (3x – 5); в) 2 (m + 1)2 – 4m.
б) 4a (a – 2) – (a – 4)2;
2. Разложите на множители.
а) х3 – 9х; б) –5a2 – 10ab – 5b2.
3. Упростите выражение
4. Разложите на множители.
а) 16х4 – 81; б) х2 – х – y2 – y.
5. Докажите, что выражение х2 – 4х + 9 при любых значениях х принимает положительные значения.
Вариант 2
1. Упростите выражение.
а) 2х (х – 3) – 3х (х + 5); в) 3 (y + 5)2 – 3y2.
б) (a + 7) (a – 1) + (a – 3)2;
2. Разложите на множители.
а) с3 – 16с; б) 3a2 – 6ab + 3b2.
3. Упростите выражение
4. Разложите на множители.
а) 81а4 – 1; б) y2 – х2 – 6х – 9.
5. Докажите, что выражение –а2 + 4а – 9 может принимать лишь отрицательные значения.
13



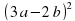

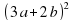
 - 24
- 24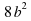
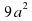 -
- 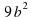


 (Г)
(Г)




