Инструкция по выполнению работы Работа состоит из двух модулей: «Алгебра» и «Геометрия». Всего в работе 24 заданий. Модуль «Алгебра» содержит шестнадцать заданий: в части 1 — четырнадцать заданий; в части 2 — два задания. Модуль «Геометрия» содержит восемь заданий: в части 1 — шесть заданий; в части 2 — два задания.
Ответы к заданиям 2, 3, 4 запишите в бланк ответов № 1 в виде одной цифры, которая соответствует номеру правильного ответа.
Для остальных заданий части 1 ответом является число или последовательность цифр. Ответ запишите в поле ответа в тексте работы, а затем перенесите в бланк ответов № 1. Если в ответе получена обыкновенная дробь, обратите её в десятичную.
Решения заданий части 2 и ответы к ним запишите на бланке ответов № 2. Задания можно выполнять в любом порядке, начиная с любого модуля. Текст задания переписывать не надо, необходимо только указать его номер.
Сначала выполняйте задания части 1. Начать советуем с тех заданий, которые вызывают у Вас меньше затруднений, затем переходите к другим заданиям. Для экономии времени пропускайте задание, которое не удаётся выполнить сразу, и переходите к следующему. Если у Вас останется время, Вы сможете вернуться к пропущенным заданиям.
При выполнении части 1 все необходимые вычисления, преобразования выполняйте в черновике. Записи в черновике не учитываются при оценивании работы. Рекомендуем внимательно читать условие и проводить проверку полученного ответа.
Баллы, полученные Вами за выполненные задания, суммируются.
Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
Желаем успеха!
Ответами к заданиям 1–20 являются цифра, число или последовательность цифр, которые следует записать в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания, начиная с первой клеточки. Если ответом является последовательность цифр, то запишите её без пробелов, запятых и других дополнительных символов. Каждый символ пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами.
Модуль «Алгебра»
Найдите значение выражения
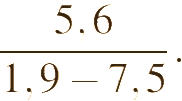
В таблице приведены нормативы по бегу на 30 метров для учащихся 9-х классов.
|
| Мальчики | Девочки | |||||
| Отметка | «5» | «4» | «3» | «5» | «4» | «3» | |
| Время, секунды | 4,6 | 4,9 | 5,3 | 5,0 | 5,5 | 5,9 | |
Какую отметку получит девочка, пробежавшая эту дистанцию за 5,36 секунды?
В ответе укажите номер правильного варианта.
1) Отметка «5».
2) Отметка «4».
3) Отметка «3».
4) Норматив не выполнен.
На координатной прямой отмечено число a.
![]()
Какое из утверждений относительно этого числа является верным?
1) a − 8 0
2) 7 − a
3) a − 3 0
4) 2 − a 0
Представьте выражение
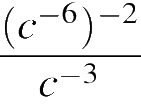 в виде степени с основанием c.
в виде степени с основанием c.
В ответе укажите номер правильного варианта.
1) ![]()
2) ![]()
3) ![]()
4) ![]()
Когда самолет находится в горизонтальном полете, подъемная сила, действующая на крылья, зависит только от скорости. На рисунке изображена эта зависимость для некоторого самолета. На оси абсцисс откладывается скорость (в километрах в час), на оси ординат – сила (в тоннах силы). Определите по рисунку, чему равна подъемная сила (в тоннах силы) при скорости 200 км/ч?

Решите уравнение
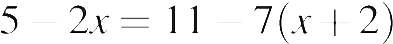
Стоимость проезда в пригородном электропоезде составляет 198 рублей. Школьникам предоставляется скидка 50%. Сколько рублей стоит проезд группы из 4 взрослых и 12 школьников?
В математические кружки города ходят школьники 5–8 классов. Распределение участников математических кружков представлено в круговой диаграмме.

Какое утверждение относительно участников кружков верно, если всего их посещают 354 школьника?
1) в кружки не ходят пятиклассники
2) восьмиклассников ходит больше, чем семиклассников
3) больше половины участников кружков учатся не в седьмом классе
4) шестиклассников меньше 88 человек
На тарелке 12 пирожков: 5 с мясом, 4 с капустой и 3 с вишней. Наташа наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.


Упростите выражение
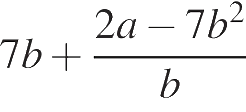 , найдите его значение при
, найдите его значение при  ;
; 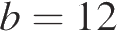 . В ответ запишите полученное число.
. В ответ запишите полученное число.
Упростите выражение
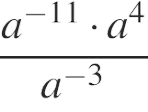 и найдите его значение при
и найдите его значение при 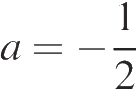 . В ответе запишите полученное число.
. В ответе запишите полученное число.
Упростите выражение
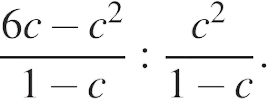 и найдите его значение
и найдите его значение
при ![]() В ответе запишите найденное значение.
В ответе запишите найденное значение.
В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) рассчитывается по формуле
 , где
, где 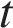 — длительность поездки, выраженная в минутах
— длительность поездки, выраженная в минутах 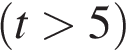 . Пользуясь этой формулой, рассчитайте стоимость 8-минутной поездки.
. Пользуясь этой формулой, рассчитайте стоимость 8-минутной поездки.
Решите уравнение
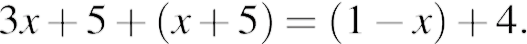
Модуль «Геометрия»
Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB = 108°. Ответ дайте в градусах.

В треугольнике ABC AC = BC. Внешний угол при вершине B равен 146°. Найдите угол C. Ответ дайте в градусах.

Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол параллелограмма.


В прямоугольнике одна сторона равна 10, другая сторона равна 12. Найдите площадь прямоугольника.
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.

Укажите номера верных утверждений.
Вертикальные углы равны.
Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.
Любая высота равнобедренного треугольника является его биссектрисой.
Если утверждений несколько, запишите их номера в порядке возрастания.
При выполнении заданий 21–24 используйте БЛАНК ОТВЕТОВ № 2. Сначала укажите номер задания, а затем запишите его решение и ответ. Пишите чётко и разборчиво.
Сократите дробь
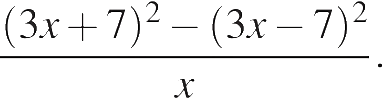
Найдите значение выражения
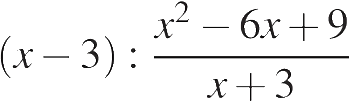 при
при 
Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 15°. Ответ дайте в градусах.

Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK = 6, CK = 10.



 (в A), по горизонтальной — время
(в A), по горизонтальной — время 










