Государственное учреждение образования
«Средняя школа № 17 г. Могилева»
Тема:
«Тригонометрия»
Разработал:
Тарасевич С.В.,
учитель математики
I квалификационной категории
Могилев 2016 г.
Содержание
Тема: “Тригонометрия”
Единичная окружность
Самостоятельная работа
Градусная и радианная мера произвольных углов
Самостоятельная работа
Определение синуса, косинуса, тангенса и котангенса произвольного угла
Самостоятельная работа
Тест
Единичная окружность
Самостоятельная работа
Найдите координаты точки, полученной поворотом точки Р (1;0) на угол -
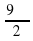 .
.
(1; 0); 4) (0; -1);
(0; 1); 5) (0; 0);
(-1; 0).
Отметьте на единичной окружности точку Аα, если:
а) α =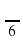 ; б) α =
; б) α = 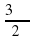 ; в) α = 5670; г) α = -
; в) α = 5670; г) α = - 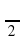 ; д) α =
; д) α = 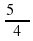 ; е) α = - 12300.
; е) α = - 12300.
В какой четверти координатной плоскости расположена точка Аα, если α равно:
а) 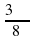 ; б) -
; б) - 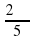 ; в) 8300; г) -12500; д) 1,8π; е) -2,3π.
; в) 8300; г) -12500; д) 1,8π; е) -2,3π.
На единичной окружности отметьте точку Аα (х; у), координаты которой удовлетворяют условию:
а) у = 0,5, х 0; б) х = 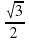 , у 0.
, у 0.
Укажите три значения градусной меры угла α, при которых абсцисса соответствующей ему точки Аα равна:
а) 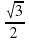 ; б) – 1; в) 0; г) -
; б) – 1; в) 0; г) - 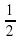 .
.
Градусная и радианная мера произвольных углов
Самостоятельная работа
Выразите в радианной мере величины углов:
а) 360; б) 2160; в) 3100; г) 3600; д) 10210.
Выразите в градусной мере величины углов:
а) 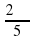 ; б)
; б) 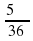 ; в) 5,3; г) -
; в) 5,3; г) - 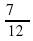 ; д) 11.
; д) 11.
Определите в какой четверти оканчивается угол α, если его радианная мера равна:
а) 9,1π; б) 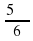 ; в) -
; в) - 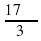 ; г) -6,3π; д) -
; г) -6,3π; д) - 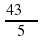 .
.
С помощью калькулятора или таблиц найдите:
а) радианные меры углов 170; 43024'; 83036'; 72012';
б) градусные меры углов 0,384; 0,48; 1,11; 1,48.
а) Найдите радианную меру центрального угла сектора, если длина соответствующей дуги равна диаметру круга.
б) Длина дуги сектора втрое меньше его периметра. Найдите радианную меру его центрального угла.
Определение синуса, косинуса, тангенса и котангенса произвольного угла
Самостоятельная работа
Могут ли синус и косинус одного и того же угла быть равными соответственно:
а) - 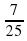 и
и 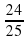 ; б) 0,4 и 0,7; в)
; б) 0,4 и 0,7; в) 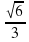 и -
и - 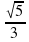 .
.
Найдите числовое значение выражения:
а) sin 0 + cos 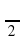 + sin2
+ sin2 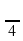 ;
;
б) 6 sin 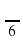 - 2 cos 0 + tg2
- 2 cos 0 + tg2 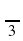 ;
;
в) 3 tg 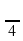 - sin2
- sin2 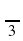 + cos2
+ cos2 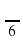 .
.
Отрицательным числом является:
а) cos 13000 ∙ sin 9300 ∙ tg 1850;
б) cos 12300 ∙ sin 4900 ∙ ctg 1250;
в) cos 13360 ∙ sin 6910 ∙ tg 2500;
г) cos 36000 ∙ sin 12900 ∙ ctg 2500.
Найдите значение выражения:
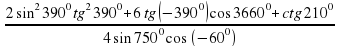 .
.
Решите уравнение:
а) sin (3x – 1) = -1;
б) cos (3x – 1) = 1.
3. Определение синуса, косинуса, тангенса и котангенса произвольного угла
3.2. Тест
1. Абсцисса точки Рα единичной окружности равна 0,3. Тогда для угла α верно равенство:
sin α = 0,3; 4) ctg α = 0,3;
cos α = 0,3; 5) cos α = - 0,3.
tg α = 0,3;
2. Укажите выражение, имеющее наименьшее значение:
sin 1; 4) cos 2;
cos 1; 5) tg 0,5.
sin 2;
3. Укажите выражение, значение которого отрицательно:
sin
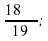 4) cos (-2970);
4) cos (-2970);cos (-490); 5) ctg
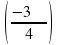 .
.tg 3;
4. Наибольшее значение выражения 7 – 2sin α принадлежит промежутку:
(1; 9); 4) (-2; 5];
(0; 7]; 5) (-2; 6].
[1; 9];
5. Если sin α = -1 и n – целое число, то верно равенство:
1) α = 8100 + 360n0; 3) α = 11700 + 360n0;
2) α = 450n0; 4) α = 2700 + 1080n0.



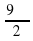 .
.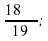 4) cos (-297
4) cos (-297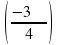 .
.



