

- Угол между двумя прямыми
Задача 1, Задача 2.
- Угол между прямой и плоскостью
Задача1. Задача 2.
- Угол между двумя плоскостями
Задача 1. Задача 2.
- Расстояние от точки до прямой
Задача 1. Задача 2.
- Расстояние от точки до плоскости
Задача 1. Задача 2.
- Расстояние между скрещивающимися прямыми
Задача 1. Задача 2.

1.Определение: Две пересекающиеся прямые образуют смежные и вертикальные углы.
Углом между двумя прямыми называется меньший из них.
Угол между перпендикулярными прямыми равен 90°. Угол между параллельными прямыми равен 0°.
 заменим одну прямую другой. DC 1 B – искомый." width="640"
заменим одну прямую другой. DC 1 B – искомый." width="640"
С 1
D 1
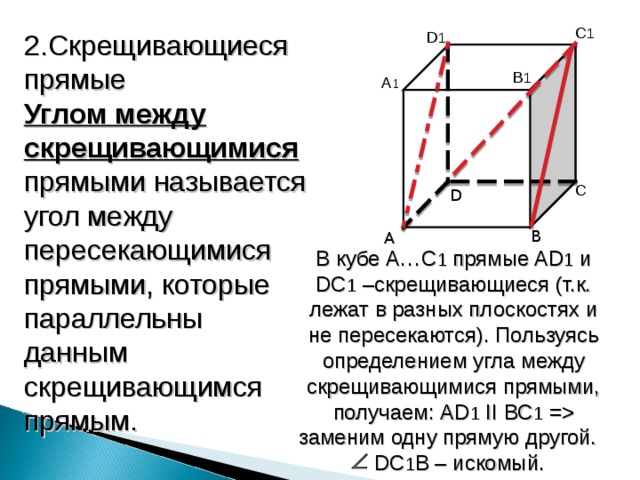
2.Скрещивающиеся прямые
Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, которые параллельны данным скрещивающимся прямым.
B 1
А 1
С
D
В
А
В кубе A…C 1 прямые AD 1 и DC 1 –скрещивающиеся (т.к. лежат в разных плоскостях и не пересекаются). Пользуясь определением угла между скрещивающимися прямыми, получаем: AD 1 II BC 1 = заменим одну прямую другой. DC 1 B – искомый.
.
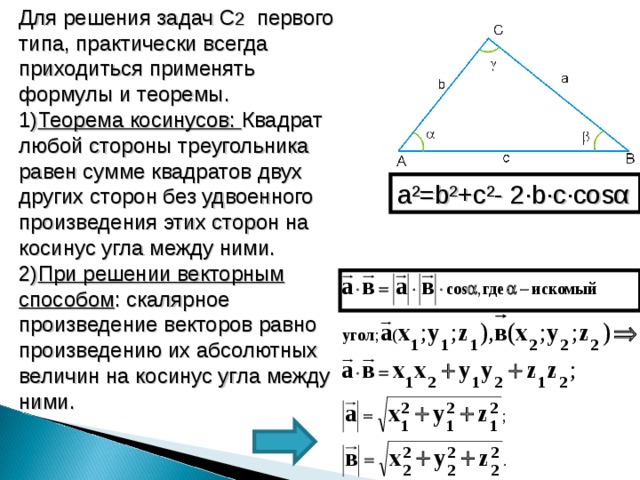
Для решения задач C 2 первого типа, практически всегда приходиться применять формулы и теоремы.
- Теорема косинусов: Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
- При решении векторным способом : скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними.
a²=b² + c²- 2∙b∙c∙cos α
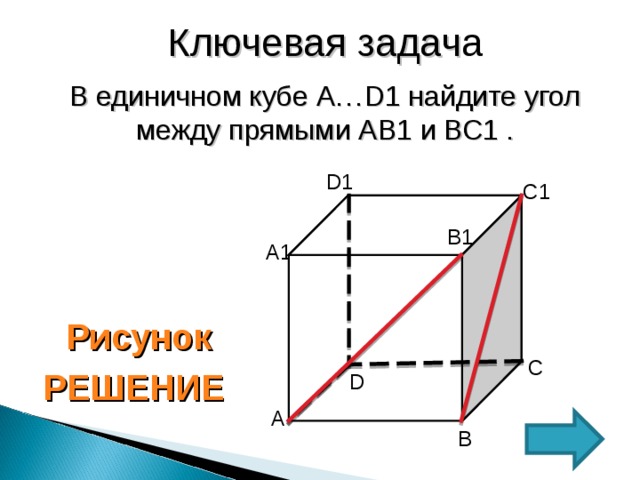
Ключевая задач а
В единичном кубе А… D 1 найдите угол между прямыми АВ1 и ВС1 .
D 1
C 1
B 1
А1
Рисунок
С
РЕШЕНИЕ
D
А
В
6
С1
D 1
B 1
А1
С
D
А
В
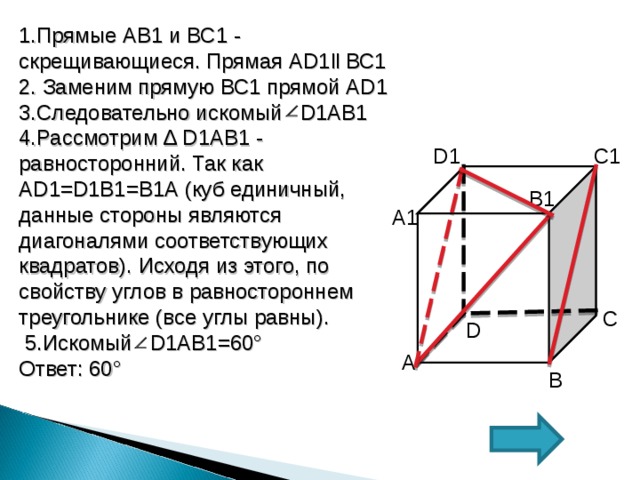
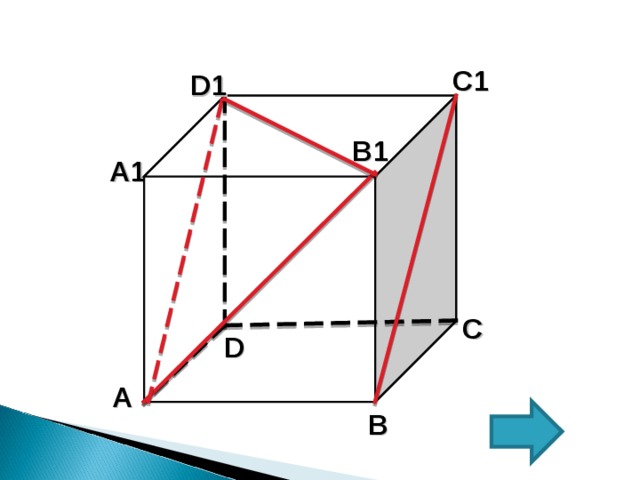
1.Прямые АВ1 и ВС1 - скрещивающиеся. Прямая А D 1 ll ВС1
2. Заменим прямую ВС1 прямой А D 1
3.Следовательно искомый D 1АВ1
4.Рассмотрим ∆ D 1АВ1 - равносторонний. Так как А D 1= D 1В1=В1А (куб единичный, данные стороны являются диагоналями соответствующих квадратов). Исходя из этого, по свойству углов в равностороннем треугольнике (все углы равны).
5.Искомый D 1АВ1=60°
Ответ: 60°
C 1
D 1
B 1
А1
С
D
А
В
8
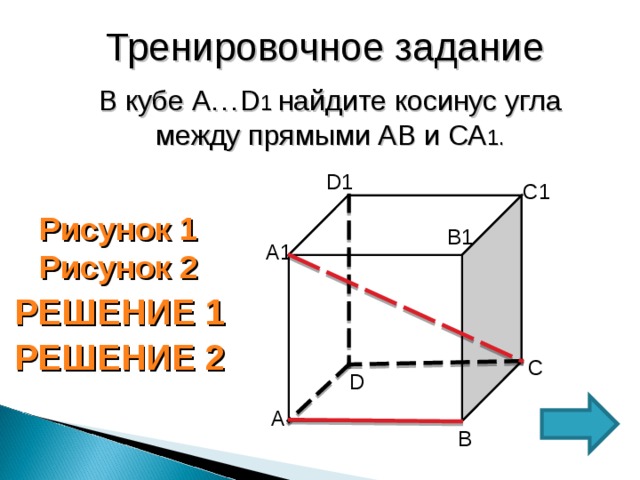
Тренировочное задание
В кубе А… D 1 найдите косинус угла между прямыми АВ и СА 1.
D 1
C 1
Рисунок 1
Рисунок 2
B 1
А1
РЕШЕНИЕ 1
РЕШЕНИЕ 2
С
D
А
В
D 1
C 1
B 1
А1
С
D
А
В
C 1
D 1
B 1
А1
С
D
А
В
 искомый угол В 1 А 1 С 3. В ∆А 1 В 1 С, так как А 1 В 1 С=90° (т.к. А 1 В 1 (ВВ 1 С 1 С), а значит по определению и любой прямой лежащей в этой плоскости А 1 В 1 В 1 С) 4. По определению косинуса: cos В 1 А 1 С= 5. А 1 В 1 =1 6. А 1 С²=1²+(√2)²=3, =А 1 С=√3 7. с os В 1 А 1 С=1/√3=√3/3 Ответ: √3/3 D 1 C 1 B 1 А1 С D А В 12" width="640"
искомый угол В 1 А 1 С 3. В ∆А 1 В 1 С, так как А 1 В 1 С=90° (т.к. А 1 В 1 (ВВ 1 С 1 С), а значит по определению и любой прямой лежащей в этой плоскости А 1 В 1 В 1 С) 4. По определению косинуса: cos В 1 А 1 С= 5. А 1 В 1 =1 6. А 1 С²=1²+(√2)²=3, =А 1 С=√3 7. с os В 1 А 1 С=1/√3=√3/3 Ответ: √3/3 D 1 C 1 B 1 А1 С D А В 12" width="640"
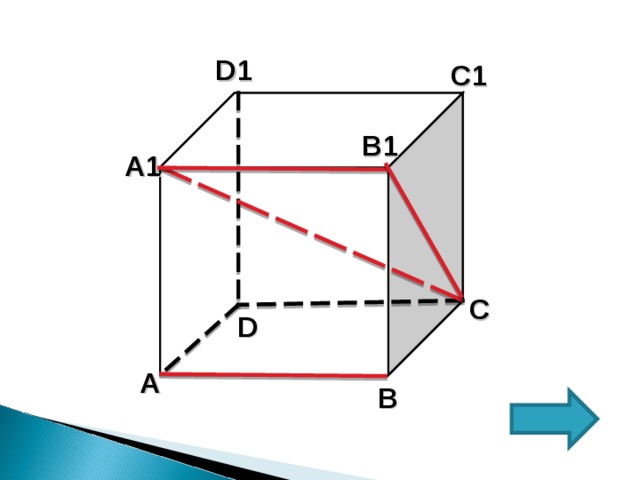
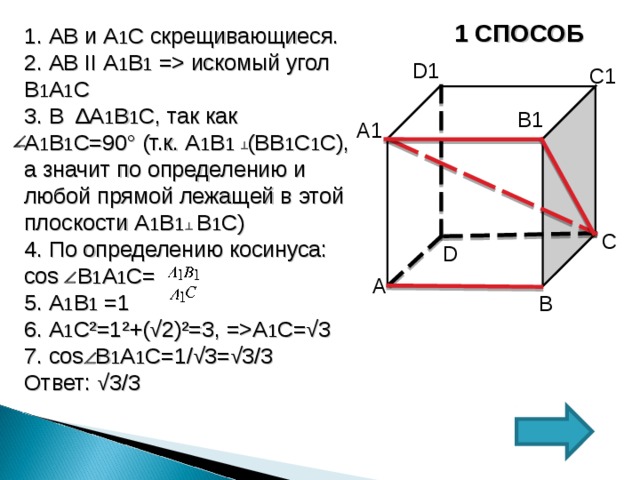
1 СПОСОБ
1. АВ и А 1 С скрещивающиеся.
2. АВ II А 1 В 1 = искомый угол В 1 А 1 С
3. В ∆А 1 В 1 С, так как
А 1 В 1 С=90° (т.к. А 1 В 1 (ВВ 1 С 1 С), а значит по определению и любой прямой лежащей в этой плоскости А 1 В 1 В 1 С)
4. По определению косинуса:
cos В 1 А 1 С=
5. А 1 В 1 =1
6. А 1 С²=1²+(√2)²=3, =А 1 С=√3
7. с os В 1 А 1 С=1/√3=√3/3
Ответ: √3/3
D 1
C 1
B 1
А1
С
D
А
В
12
 А 1 С (1;1;-1) 5. Пусть α угол между АВ и А 1 С, тогда cos α = АВ∙А 1 С=1+0+0=1 I АВ I = I А 1 С I = 6. с os α =1/(1∙√3)=1/√3=√3/3 Ответ: √3/3 2 СПОСОБ C 1 D 1 B 1 А1 С D А В" width="640"
А 1 С (1;1;-1) 5. Пусть α угол между АВ и А 1 С, тогда cos α = АВ∙А 1 С=1+0+0=1 I АВ I = I А 1 С I = 6. с os α =1/(1∙√3)=1/√3=√3/3 Ответ: √3/3 2 СПОСОБ C 1 D 1 B 1 А1 С D А В" width="640"
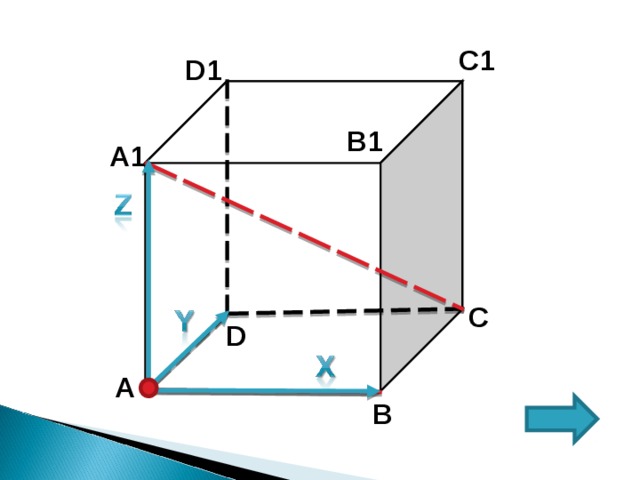
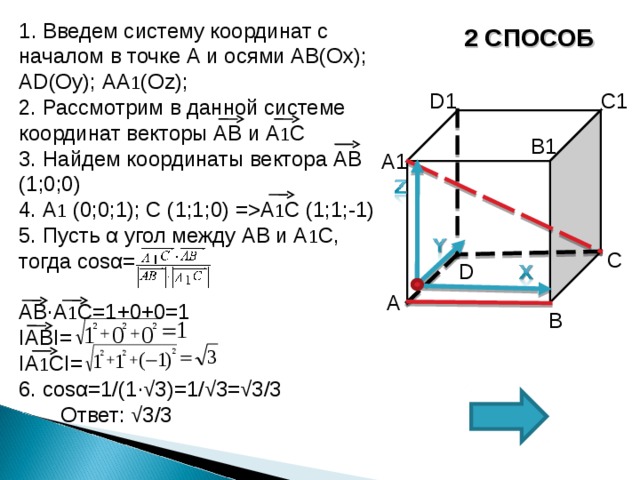
1 . Введем систему координат с началом в точке А и осями АВ(Ох); А D (Оу); АА 1 (О z );
2. Рассмотрим в данной системе координат векторы АВ и А 1 С
3. Найдем координаты вектора АВ (1;0;0)
4. А 1 (0;0;1); С (1;1;0) =А 1 С (1;1;-1)
5. Пусть α угол между АВ и А 1 С,
тогда cos α =
АВ∙А 1 С=1+0+0=1
I АВ I =
I А 1 С I =
6. с os α =1/(1∙√3)=1/√3=√3/3
Ответ: √3/3
2 СПОСОБ
C 1
D 1
B 1
А1
С
D
А
В

1 . Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость.
2. Угол между взаимно перпендикулярными прямой и плоскостью равен 90 .
3. Если прямая параллельна плоскости (или лежит в ней), то угол между ними считается равным 0 .
В
а
С
α י
А
α
а ∩ α =А
ВС α
ВАС – искомый угол
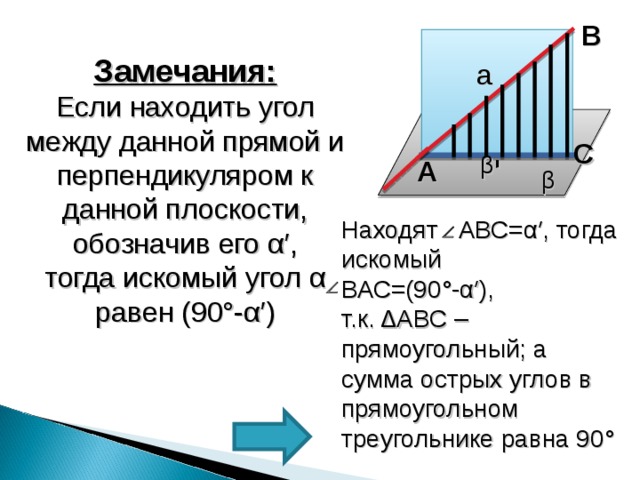
Замечания:
Если находить угол между данной прямой и перпендикуляром к данной плоскости, обозначив его α′ ,
тогда искомый угол α равен (90°- α′ )
В
а
С
β י
А
β
Находят АВС= α′ , тогда искомый ВАС=(90°- α′ ),
т.к. ∆АВС – прямоугольный; а сумма острых углов в прямоугольном треугольнике равна 90°
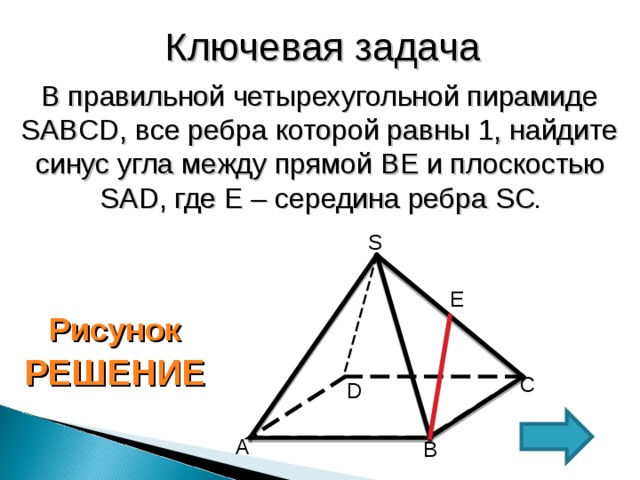
Ключевая задача
В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1, найдите синус угла между прямой BE и плоскостью SAD , где Е – середина ребра SC .
S
E
Рисунок
РЕШЕНИЕ
C
D
А
B
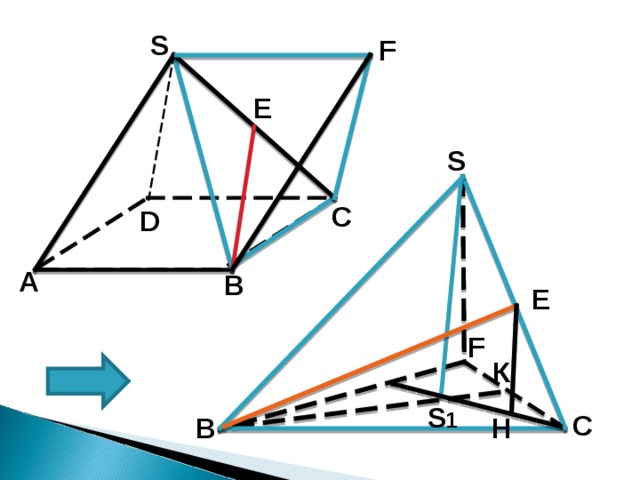
S
F
E
S
C
D
А
B
E
F
К
S 1
C
B
H
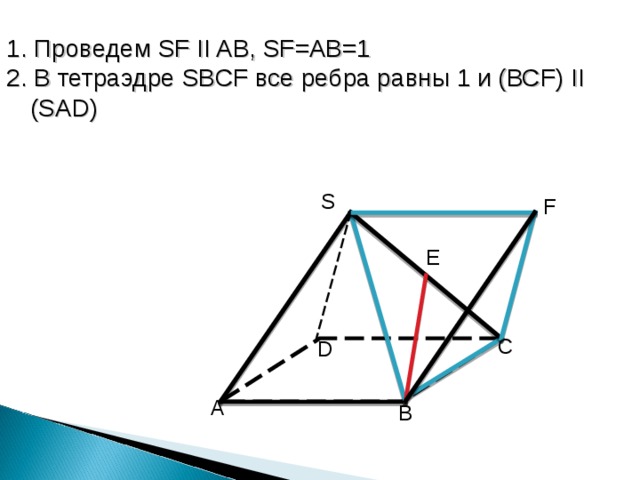
1. Проведем SF II AB , SF = AB =1
2. В тетраэдре SB С F все ребра равны 1 и (ВС F) II (SAD)
S
F
E
C
D
А
B
 B К=(а∙√3)/2, т.е. B К= √3/2, = R 1 = √3/3 6. SS1= SS1= ; SS 1 = √6/3 ; EH =√6/6 7. EBH – искомый, sin B=EH/BE , BE – медиана, высота равностороннего треугольника, = BE = √3/2 8. sin B =(√6∙2)/(6∙√3)=√2/3 Ответ: √2/3 S E F К S1 B C H" width="640"
B К=(а∙√3)/2, т.е. B К= √3/2, = R 1 = √3/3 6. SS1= SS1= ; SS 1 = √6/3 ; EH =√6/6 7. EBH – искомый, sin B=EH/BE , BE – медиана, высота равностороннего треугольника, = BE = √3/2 8. sin B =(√6∙2)/(6∙√3)=√2/3 Ответ: √2/3 S E F К S1 B C H" width="640"
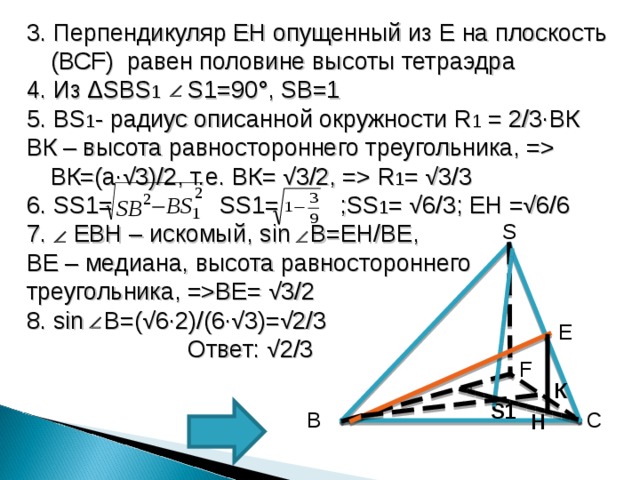
3. Перпендикуляр EH опущенный из Е на плоскость (ВС F) равен половине высоты тетраэдра
4. Из ∆ SBS 1 S 1=90°, SB =1
5. BS 1 - радиус описанной окружности R 1 = 2/3∙ B К
B К – высота равностороннего треугольника, = B К=(а∙√3)/2, т.е. B К= √3/2, = R 1 = √3/3
6. SS1= SS1= ; SS 1 = √6/3 ; EH =√6/6
7. EBH – искомый, sin B=EH/BE ,
BE – медиана, высота равностороннего
треугольника, = BE = √3/2
8. sin B =(√6∙2)/(6∙√3)=√2/3
Ответ: √2/3
S
E
F
К
S1
B
C
H
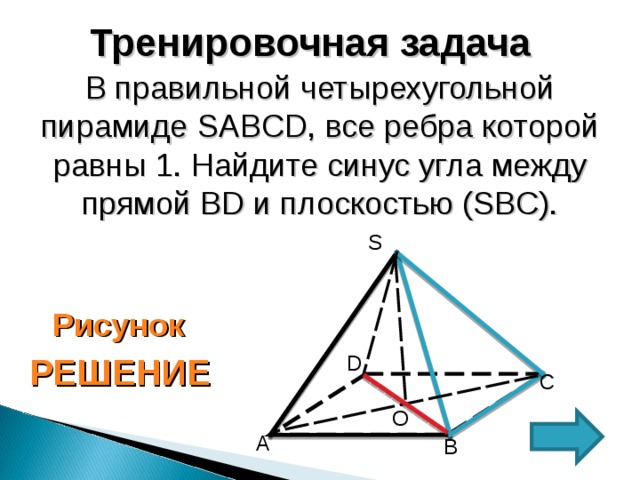
Тренировочная задача
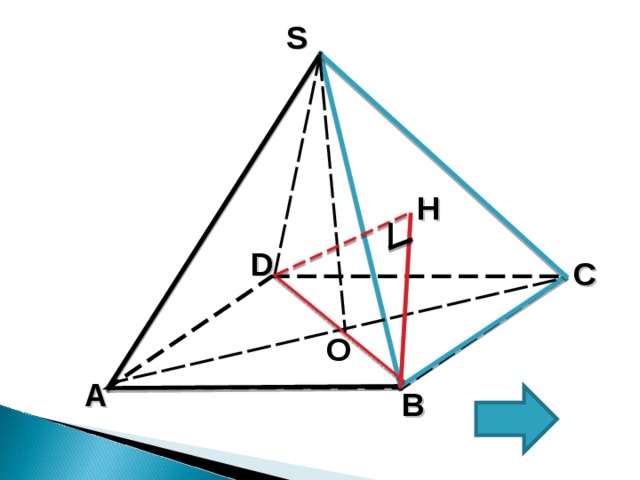
В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1. Найдите синус угла между прямой BD и плоскостью (SBC).
S
Рисунок
D
РЕШЕНИЕ
C
O
А
B
S
H
D
C
O
А
B
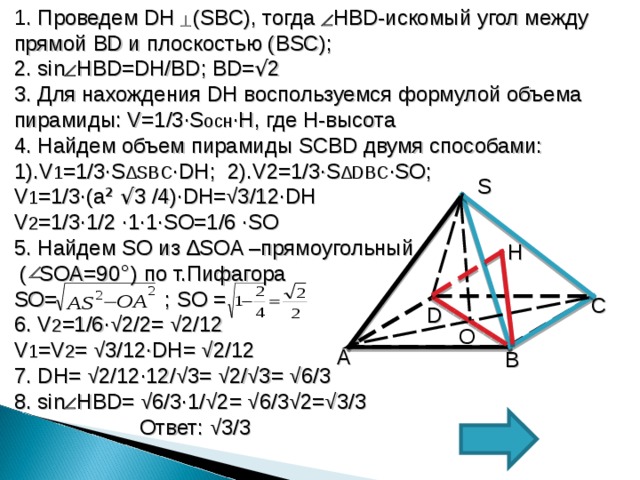
1 . Проведем DH (SBC) , тогда HBD -искомый угол между прямой BD и плоскостью ( BSC) ;
2. sin HBD=DH/BD ; BD= √ 2
3. Для нахождения DH воспользуемся формулой объема пирамиды: V=1/3∙S осн ∙ H , где H -высота
4. Найдем объем пирамиды SCBD двумя способами:
1). V 1 =1/3∙S ∆ SBC ∙DH ; 2). V2=1/3∙S ∆ DBC ∙SO ;
V 1 =1/3∙ ( a ² √ 3 /4 ) ∙DH= √ 3/12∙DH
V 2 =1/3∙1/2 ∙ 1 ∙1∙SO=1/6 ∙SO
5. Найдем SO из ∆ SOA –прямоугольный
( SOA=90 ° ) по т.Пифагора
SO= ; SO =
6. V 2 =1/6∙ √ 2/2= √ 2/12
V 1 =V 2 = √ 3/12∙DH= √ 2/12
7. DH= √ 2/12∙12/ √ 3= √ 2/ √ 3= √ 6/3
8. sin HBD= √ 6/3∙1/ √ 2= √ 6/3 √ 2= √ 3/3
Ответ: √ 3/3
S
H
C
D
O
А
B
![Двугранный угол , образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру. Величина двугранного угла принадлежит промежутку (0°; 180°). Величина угла между пересекающимися плоскостями принадлежит промежутку (0°; 90°]. Угол между двумя параллельными плоскостями равен 0° .](http://fsd.intolimp.org/html/2017/09/18/i_59bfd35d14a4c/img_phpRVR3Z4_S2_22.jpg)
Двугранный угол , образованный полуплоскостями измеряется величиной его линейного угла,
получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру.
Величина двугранного угла принадлежит промежутку (0°; 180°).
Величина угла между пересекающимися плоскостями принадлежит промежутку (0°; 90°].
Угол между двумя параллельными плоскостями равен 0° .
Ключевая задача
В единичном кубе А…D1 найдите тангенс угла между плоскостями (АА1D) и (BDC1)
Рисунок
РЕШЕНИЕ
E
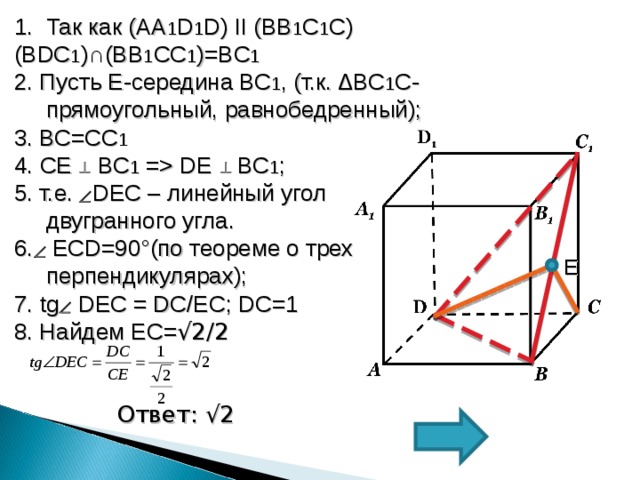
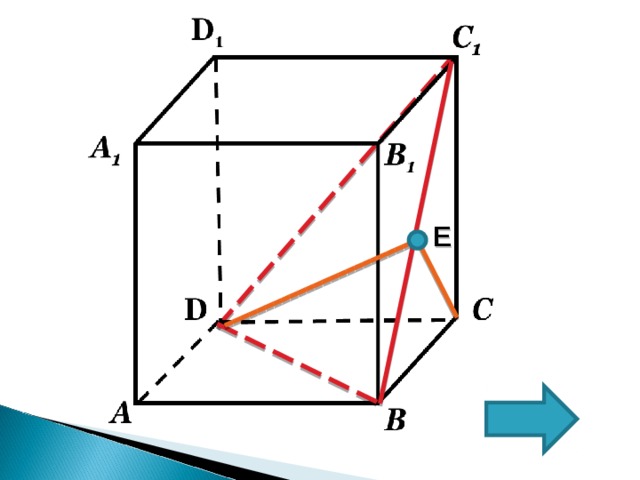
- Так как (АА 1 D 1 D) II ( BB 1 C 1 С)
( BDC 1 )∩(BB 1 CC 1 )=BC 1
2. Пусть Е-середина ВС 1 , (т.к. ∆ BC 1 C- прямоугольный, равнобедренный);
3. ВС=С C 1
4. CE BC 1 = DE BC 1 ;
5. т.е. DEC – линейный угол двугранного угла.
6. ECD=90°( по теореме о трех перпендикулярах);
7. tg DEC = DC/EC ; DC=1
8. Найдем EC = √2/2
Ответ: √2
E
Тренировочная задача
В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1. Найдите косинус двугранного угла, образованного гранями ( SBC) и (SCD)
S
Рисунок
РЕШЕНИЕ
C
D
А
B
S
K
D
С
O
А
B
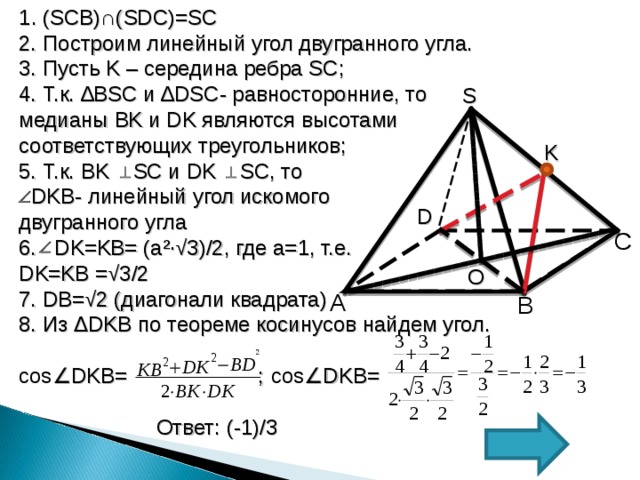
1 . (SCB)∩(SDC)=SC
2. Построим линейный угол двугранного угла.
3. Пусть K – середина ребра SC ;
4. Т.к. ∆BSC и ∆ DSC - равносторонние, то медианы BK и DK являются высотами соответствующих треугольников;
5. Т.к. BK SC и DK SC , то
DKB- линейный угол искомого
двугранного угла
6. DK=KB= (a²∙√3)/2 , где а=1, т.е.
DK=KB =√3/2
7. DB=√2 (диагонали квадрата)
8. Из ∆ DKB по теореме косинусов найдем угол.
cos ∠ DKB= ; cos ∠ DKB=
Ответ: (-1)/3
S
K
D
C
O
А
B
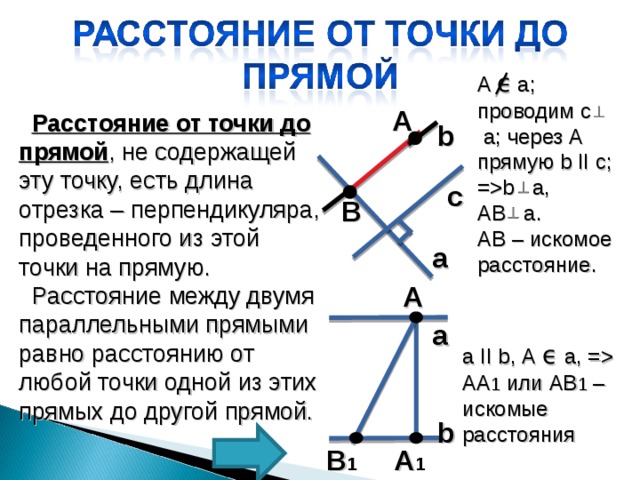 b a , AB а . AB – искомое расстояние. A Расстояние от точки до прямой , не содержащей эту точку, есть длина отрезка – перпендикуляра, проведенного из этой точки на прямую. Расстояние между двумя параллельными прямыми равно расстоянию от любой точки одной из этих прямых до другой прямой. b с B a A a a II b, А ϵ а, = АА 1 или АВ 1 – искомые расстояния b A 1 B 1" width="640"
b a , AB а . AB – искомое расстояние. A Расстояние от точки до прямой , не содержащей эту точку, есть длина отрезка – перпендикуляра, проведенного из этой точки на прямую. Расстояние между двумя параллельными прямыми равно расстоянию от любой точки одной из этих прямых до другой прямой. b с B a A a a II b, А ϵ а, = АА 1 или АВ 1 – искомые расстояния b A 1 B 1" width="640"
A ϵ а; проводим с
а; через А прямую b II с; = b a ,
AB а .
AB – искомое расстояние.
A
Расстояние от точки до прямой , не содержащей эту точку, есть длина отрезка – перпендикуляра, проведенного из этой точки на прямую.
Расстояние между двумя параллельными прямыми равно расстоянию от любой точки одной из этих прямых до другой прямой.
b
с
B
a
A
a
a II b, А ϵ а, = АА 1 или АВ 1 – искомые расстояния
b
A 1
B 1
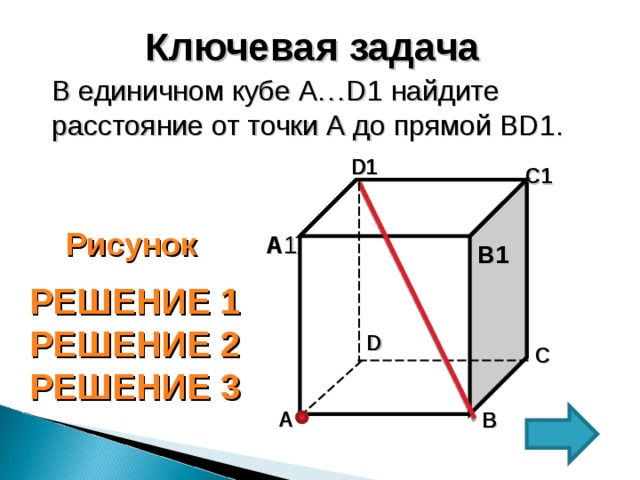
Ключевая задача
В единичном кубе А…D 1 найдите расстояние от точки А до прямой BD 1 .
D
D 1
C 1
Рисунок
A 1
B 1
РЕШЕНИЕ 1
РЕШЕНИЕ 2
РЕШЕНИЕ 3
D
C
A
B
B
D 1
С1
A 1
B 1
H
D
C
A
B
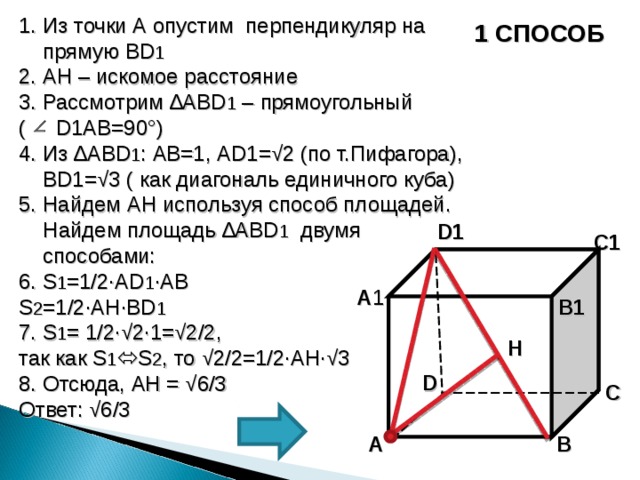
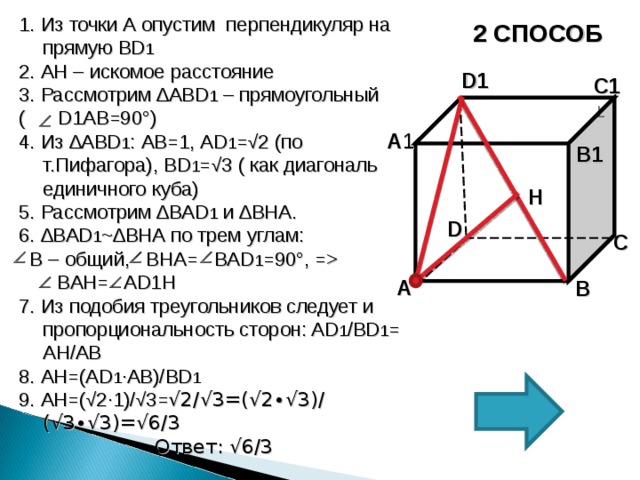
1. Из точки А опустим перпендикуляр на прямую BD 1
2. AH – искомое расстояние
3. Рассмотрим ∆ ABD 1 – прямоугольный
( D1AB =90°)
4. Из ∆ ABD 1 : AB =1, AD1 =√2 (по т.Пифагора), BD1 =√3 ( как диагональ единичного куба)
5. Найдем AH используя способ площадей. Найдем площадь ∆ ABD 1 двумя способами:
6. S 1 =1/2∙AD 1 ∙AB
S 2 =1/2∙AH∙BD 1
7. S 1 = 1/2∙√2∙1=√2/2 ,
так как S 1 S 2 , то √2/2=1/2∙AH∙√3
8. Отсюда, AH = √ 6/3
Ответ: √6/3
1 СПОСОБ
D 1
C 1
A 1
B 1
H
D
C
A
B
30
 BAH= AD1H 7. Из подобия треугольников следует и пропорциональность сторон: AD 1 /BD 1 = AH/AB 8 . AH =( AD 1 ∙AB )/ BD 1 9. А H = ( √ 2∙1)/√3= √2/√3=(√2∙√3)/(√3∙√3)=√6/3 Ответ: √6/3 2 СПОСОБ D 1 C 1 A 1 B 1 H D C H A B" width="640"
BAH= AD1H 7. Из подобия треугольников следует и пропорциональность сторон: AD 1 /BD 1 = AH/AB 8 . AH =( AD 1 ∙AB )/ BD 1 9. А H = ( √ 2∙1)/√3= √2/√3=(√2∙√3)/(√3∙√3)=√6/3 Ответ: √6/3 2 СПОСОБ D 1 C 1 A 1 B 1 H D C H A B" width="640"
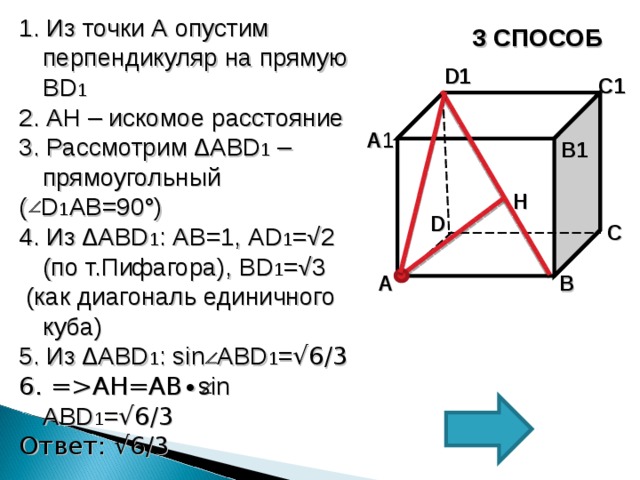
1. Из точки А опустим перпендикуляр на прямую BD 1
2. AH – искомое расстояние
3. Рассмотрим ∆ ABD 1 – прямоугольный
( D1AB =90°)
4. Из ∆ ABD 1 : AB =1, AD 1 =√2 (по т.Пифагора), BD 1 =√3 ( как диагональ единичного куба)
5. Рассмотрим ∆ BAD 1 и ∆ BHA .
6. ∆ BAD 1 ~ ∆ BHA по трем углам:
B – общий, BHA= BAD 1 =90°, =
BAH= AD1H
7. Из подобия треугольников следует и пропорциональность сторон: AD 1 /BD 1 = AH/AB
8 . AH =( AD 1 ∙AB )/ BD 1
9. А H = ( √ 2∙1)/√3= √2/√3=(√2∙√3)/(√3∙√3)=√6/3
Ответ: √6/3
2 СПОСОБ
D 1
C 1
A 1
B 1
H
D
C
H
A
B
 AH=AB∙ sin ABD 1 = √6/3 Ответ: √6/3 3 СПОСОБ D 1 C 1 A 1 B 1 H D C A B" width="640"
AH=AB∙ sin ABD 1 = √6/3 Ответ: √6/3 3 СПОСОБ D 1 C 1 A 1 B 1 H D C A B" width="640"
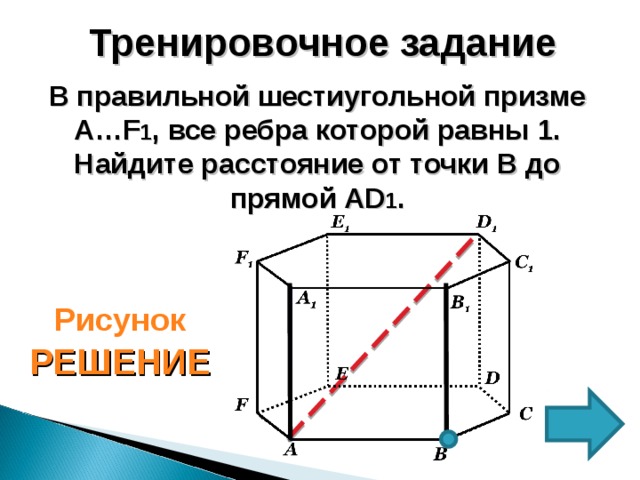
1. Из точки А опустим перпендикуляр на прямую BD 1
2. AH – искомое расстояние
3. Рассмотрим ∆ ABD 1 – прямоугольный
( D 1 AB =90°)
4. Из ∆ ABD 1 : AB =1, AD 1 =√2 (по т.Пифагора), BD 1 =√3
(как диагональ единичного куба)
5. Из ∆ ABD 1 : sin ABD 1 = √6/3
6 . = AH=AB∙ sin ABD 1 = √6/3
Ответ: √6/3
3 СПОСОБ
D 1
C 1
A 1
B 1
H
D
C
A
B
Тренировочное задание
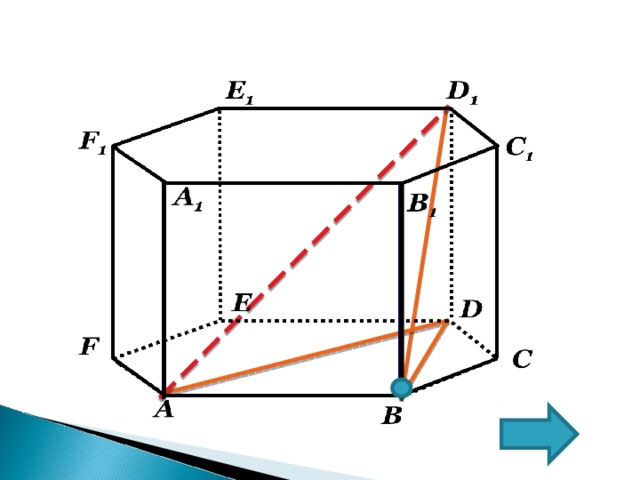
В правильной шестиугольной призме A…F 1 , все ребра которой равны 1. Найдите расстояние от точки B до прямой AD 1 .
Рисунок
РЕШЕНИЕ
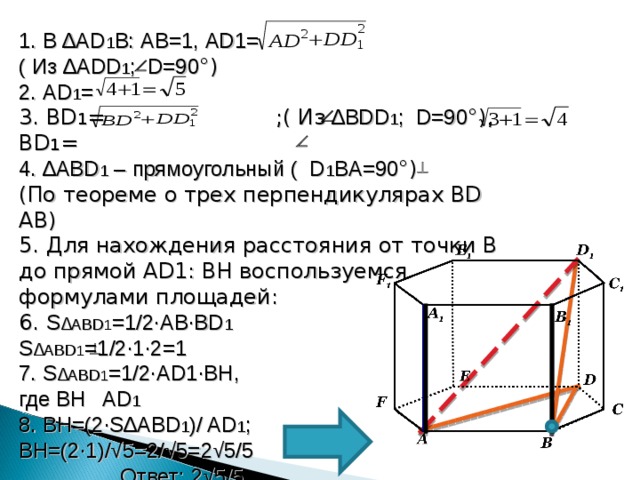
1. В ∆ AD 1 B : AB=1 , AD1=
( Из ∆ ADD 1 ; D=90 °)
2. AD 1 =
3. BD 1 = ;( Из ∆ BDD 1 ; D=90 °) , BD 1 =
4. ∆ ABD 1 – прямоугольный ( D 1 BA=90 °)
( По теореме о трех перпендикулярах BD AB)
5. Для нахождения расстояния от точки В до прямой AD1 : BH воспользуемся формулами площадей:
6. S ∆ ABD 1 =1/2∙AB∙BD 1
S ∆ ABD 1 =1/2∙1∙2=1
7. S ∆ ABD 1 =1/2∙AD1∙BH ,
где BH AD 1
8. BH=(2∙S ∆ ABD 1 )/ AD 1 ;
BH=(2∙1)/√5=2/√5=2√5/5
Ответ: 2√5/5
A
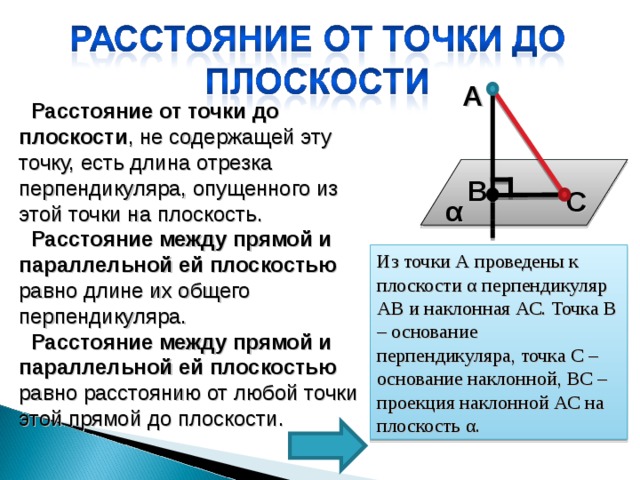
Расстояние от точки до плоскости , не содержащей эту точку, есть длина отрезка перпендикуляра, опущенного из этой точки на плоскость.
Расстояние между прямой и параллельной ей плоскостью равно длине их общего перпендикуляра.
Расстояние между прямой и параллельной ей плоскостью равно расстоянию от любой точки этой прямой до плоскости.
B
C
α
Из точки А проведены к плоскости α перпендикуляр АВ и наклонная АС. Точка В – основание перпендикуляра, точка С – основание наклонной, ВС – проекция наклонной АС на плоскость α .
 с АС; Аналогично доказывается и обратное утверждение." width="640"
с АС; Аналогично доказывается и обратное утверждение." width="640"
А
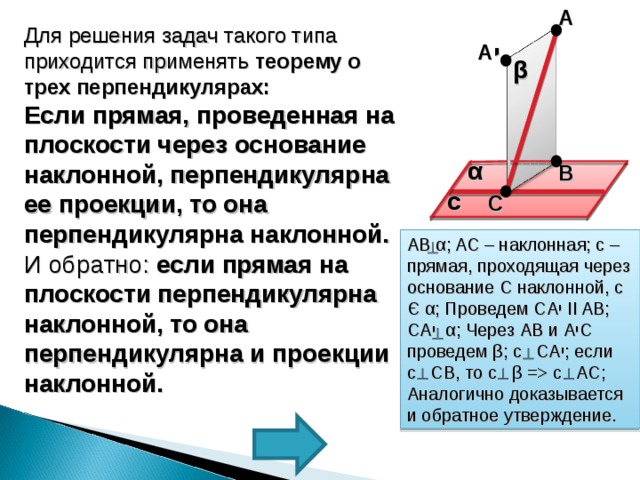
Для решения задач такого типа приходится применять теорему о трех перпендикулярах:
Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной. И обратно: если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.
A י
β
α
B
c
C
AB α ; AC – наклонная; с – прямая, проходящая через основание С наклонной, с Є α ; Проведем С A י II AB ; С A י α ; Через AB и A י С проведем β ; с СА י ; если
с СВ, то с β = с АС;
Аналогично доказывается и обратное утверждение.
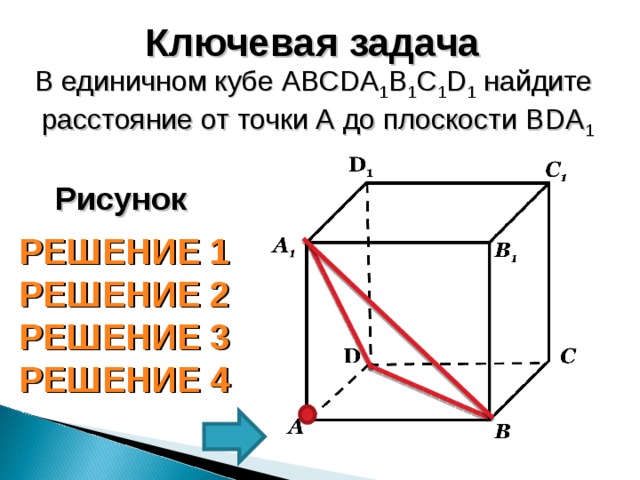
Ключевая задача
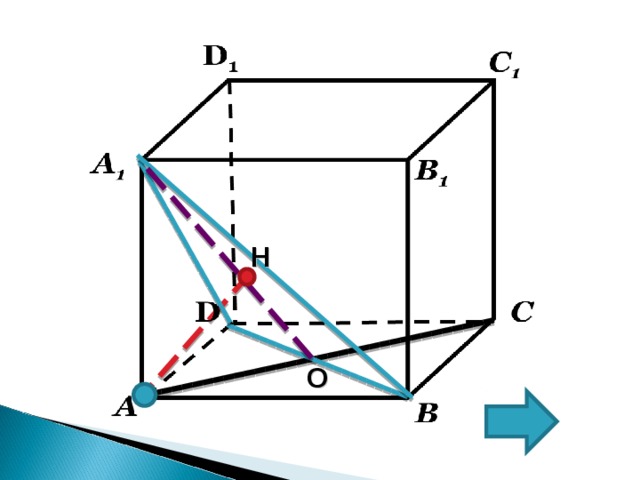
В единичном кубе АВС D А 1 В 1 С 1 D 1 найдите
расстояние от точки А до плоскости В D А 1
Рисунок
РЕШЕНИЕ 1
РЕШЕНИЕ 2
РЕШЕНИЕ 3
РЕШЕНИЕ 4
H
O
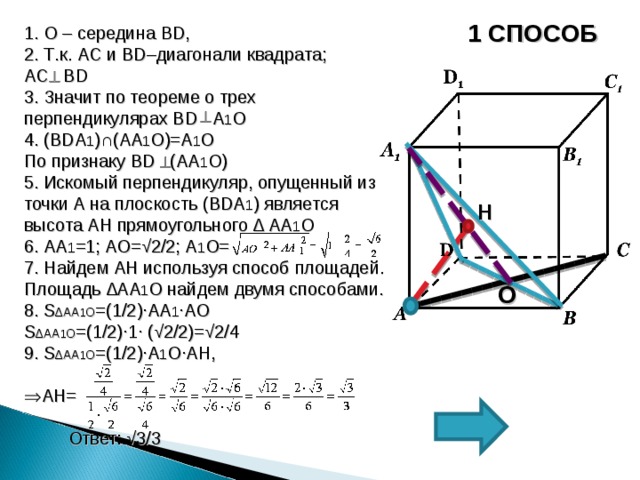
1 СПОСОБ
1. О – середина BD ,
2. Т . к. AC и BD –диагонали квадрата;
AC BD
3. Значит по теореме о трех перпендикулярах BD A 1 О
4. ( BDA 1 ) ∩ (АА 1 О)=А 1 О
По признаку BD (А A 1 О)
5. Искомый перпендикуляр, опущенный из точки А на плоскость ( BDA 1 ) является высота AH прямоугольного ∆ А A 1 О
6. АА 1 =1; АО=√2/2; А 1 О=
7. Найдем А H используя способ площадей.
Площадь ∆АА 1 О найдем двумя способами.
8. S ∆АА 1 О =(1/2)∙ АА 1 ∙ А O
S ∆АА 1 О =(1/2)∙1∙ ( √ 2/2)=√2/4
9. S ∆АА 1 О =(1/2)∙ А 1 О ∙ А H ,
- А H=
Ответ: √3/3
H
О
 AH=A О ∙sin A О H=√ 3 /3 Ответ: √ 3 /3 2 СПОСОБ H О" width="640"
AH=A О ∙sin A О H=√ 3 /3 Ответ: √ 3 /3 2 СПОСОБ H О" width="640"
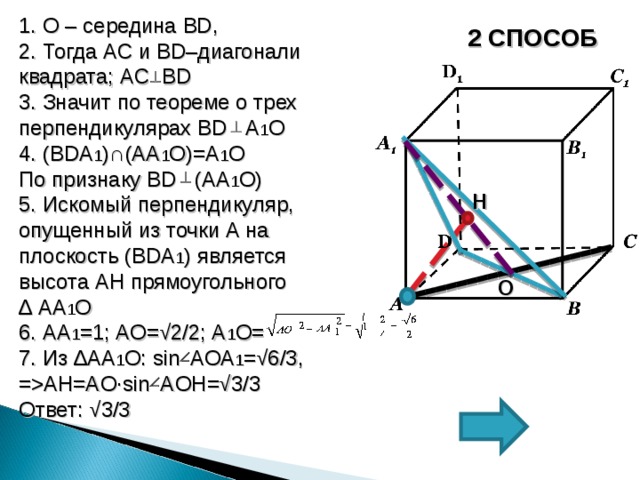
1. О – середина BD ,
2. Тогда AC и BD –диагонали квадрата; AC BD
3. Значит по теореме о трех перпендикулярах BD A 1 О
4. ( BDA 1 ) ∩ (АА 1 О)=А 1 О
По признаку BD (А A 1 О)
5. Искомый перпендикуляр, опущенный из точки А на плоскость ( BDA 1 ) является высота AH прямоугольного
∆ А A 1 О
6. АА 1 =1; АО=√2/2; А 1 О=
7. Из ∆ A А 1 О: sin A ОА 1 =√6/3 ,
= AH=A О ∙sin A О H=√ 3 /3
Ответ: √ 3 /3
2 СПОСОБ
H
О
 HA О = A А 1H 7. Из подобия треугольников следует и пропорциональность сторон: A А 1/ ОА 1= AH/A О 8 . AH =( A А 1∙A О)/А 1 О 9. А H = Ответ: √3/3 3 СПОСОБ H О" width="640"
HA О = A А 1H 7. Из подобия треугольников следует и пропорциональность сторон: A А 1/ ОА 1= AH/A О 8 . AH =( A А 1∙A О)/А 1 О 9. А H = Ответ: √3/3 3 СПОСОБ H О" width="640"
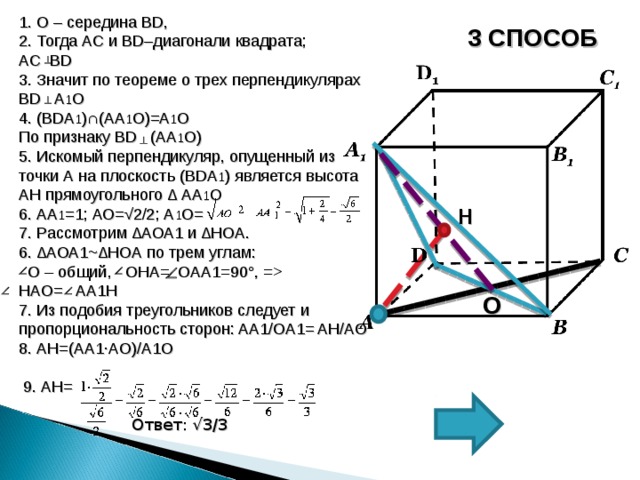
1. О – середина BD ,
2. Тогда AC и BD –диагонали квадрата;
AC BD
3. Значит по теореме о трех перпендикулярах BD A 1 О
4. ( BDA 1 ) ∩ (АА 1 О)=А 1 О
По признаку BD (А A 1 О)
5. Искомый перпендикуляр, опущенный из точки А на плоскость ( BDA 1 ) является высота AH прямоугольного ∆ А A 1 О
6. АА 1 =1; АО=√2/2; А 1 О=
7. Рассмотрим ∆АОА 1 и ∆ H О A .
6. ∆АОА 1~ ∆ H О A по трем углам:
О – общий, О HA= О A А 1=90°, = HA О = A А 1H
7. Из подобия треугольников следует и пропорциональность сторон: A А 1/ ОА 1= AH/A О
8 . AH =( A А 1∙A О)/А 1 О
9. А H =
Ответ: √3/3
3 СПОСОБ
H
О
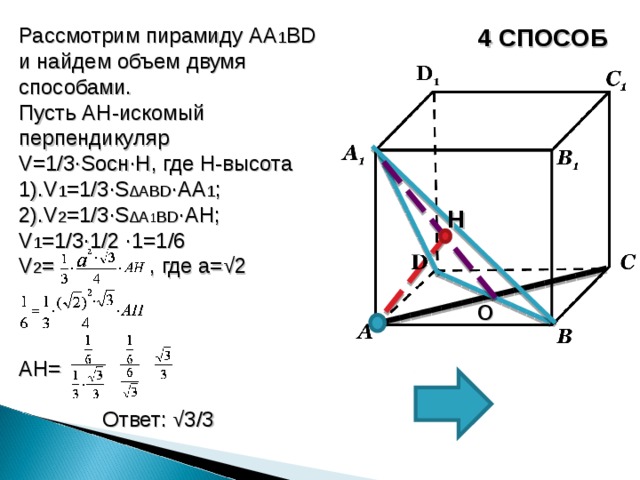
Рассмотрим пирамиду AA 1 BD и найдем объем двумя способами.
Пусть AH -искомый перпендикуляр
V=1/3∙S осн∙ H , где H -высота
1). V 1 =1/3∙S ∆А BD ∙AA 1 ; 2). V 2 =1/3∙S ∆ A 1 BD ∙AH ;
V 1 =1/3∙1/2 ∙ 1 =1/6
V 2 = , где а=√2
AH =
Ответ: √3/3
4 СПОСОБ
H
О
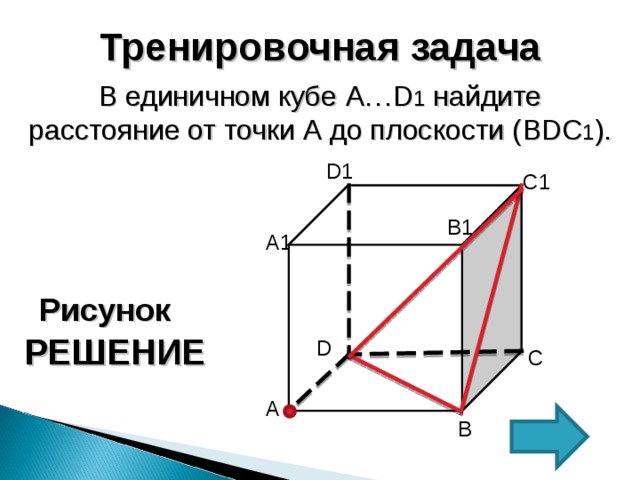
Тренировочная задача
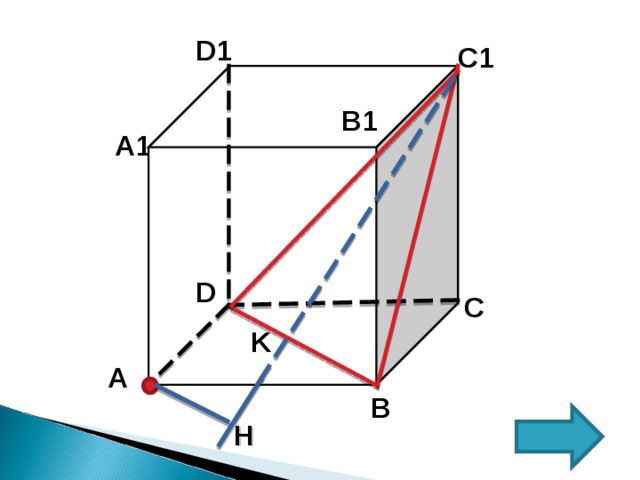
В единичном кубе A … D 1 найдите расстояние от точки А до плоскости ( BDC 1 ).
D1
C1
B1
А 1
Рисунок
РЕШЕНИЕ
D
С
А
В
D1
C1
B1
А 1
D
С
K
А
В
H
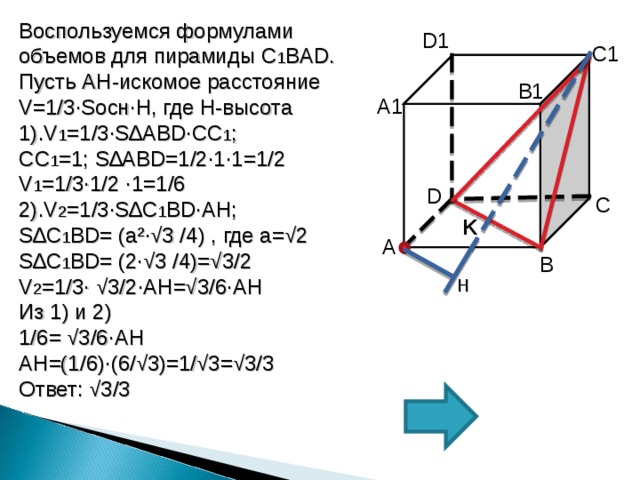
Воспользуемся формулами объемов для пирамиды C 1 BAD .
Пусть AH -искомое расстояние
V=1/3∙S осн∙ H , где H -высота
1). V 1 =1/3∙S ∆А BD∙ СС 1 ;
СС 1 =1; S ∆А BD =1/2∙1∙1=1/2
V 1 =1/3∙1/2 ∙ 1 =1/6
2). V 2 =1/3∙S ∆С 1 BD∙AH ;
S ∆С 1 BD = ( a² ∙√ 3 /4 ) , где а=√2
S ∆С 1 BD = (2∙√ 3 /4 )=√3/2
V 2 =1/3∙ √3/2 ∙AH =√3/6 ∙AH
Из 1) и 2)
1/6= √3/6 ∙AH
AH =(1/6)∙(6/√3)=1/√3=√3/3
Ответ: √3/3
D1
C1
B1
А 1
D
С
K
А
В
H
β
А
а
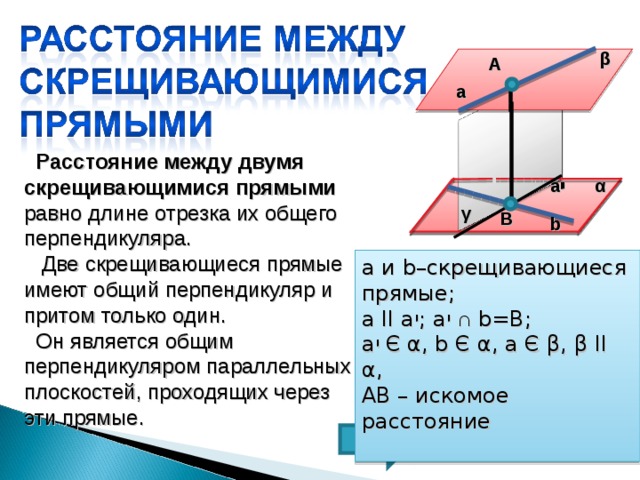
Расстояние между двумя скрещивающимися прямыми равно длине отрезка их общего перпендикуляра.
Две скрещивающиеся прямые имеют общий перпендикуляр и притом только один.
Он является общим перпендикуляром параллельных плоскостей, проходящих через эти прямые.
а י
α
γ
В
b
а и b –скрещивающиеся прямые;
а II а י ; а י ∩ b=B ;
a י Є α , b Є α , a Є β , β II α ,
АВ – искомое расстояние
Ключевая задача
В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1. Найдите расстояние между прямыми SA и BC .
S
Рисунок
РЕШЕНИЕ
C
D
А
B
S
H
D
C
E
F
O
А
B
 расстояние между скрещивающимися прямыми SA и ВС равно расстоянию от прямой ВС до плоскости ( SAD ); 4. Пусть E и F соответственно середины ребер AD и BC . Тогда искомым перпендикуляром будет высота FH ∆ SEF . 5. В ∆ SEF : EF =АВ=1; SE=SF -высоты равнобедренных ∆ SAD и ∆ SBC соответственно, = SE=SF =√3/2 SO – высота четырехугольной пирамиды из прямоугольного ∆ SOF по теореме Пифагора: SO =√2/2. 6. Найдем FH используя способ площадей. Площадь ∆ SEF найдем двумя способами. 7. S ∆ SEF=(1/2)∙EF∙SO S ∆ SEF=(1/2)∙1∙ ( √ 2/2)=√2/4 8. S ∆ SEF=(1/2)∙SE∙HF , = HF=(√2/4)/((1/2)∙√3/2)=(√2/4)/(√3/4)= = √2/√3=√6/3 . Ответ: √6/3 S H D C E O F А B" width="640"
расстояние между скрещивающимися прямыми SA и ВС равно расстоянию от прямой ВС до плоскости ( SAD ); 4. Пусть E и F соответственно середины ребер AD и BC . Тогда искомым перпендикуляром будет высота FH ∆ SEF . 5. В ∆ SEF : EF =АВ=1; SE=SF -высоты равнобедренных ∆ SAD и ∆ SBC соответственно, = SE=SF =√3/2 SO – высота четырехугольной пирамиды из прямоугольного ∆ SOF по теореме Пифагора: SO =√2/2. 6. Найдем FH используя способ площадей. Площадь ∆ SEF найдем двумя способами. 7. S ∆ SEF=(1/2)∙EF∙SO S ∆ SEF=(1/2)∙1∙ ( √ 2/2)=√2/4 8. S ∆ SEF=(1/2)∙SE∙HF , = HF=(√2/4)/((1/2)∙√3/2)=(√2/4)/(√3/4)= = √2/√3=√6/3 . Ответ: √6/3 S H D C E O F А B" width="640"
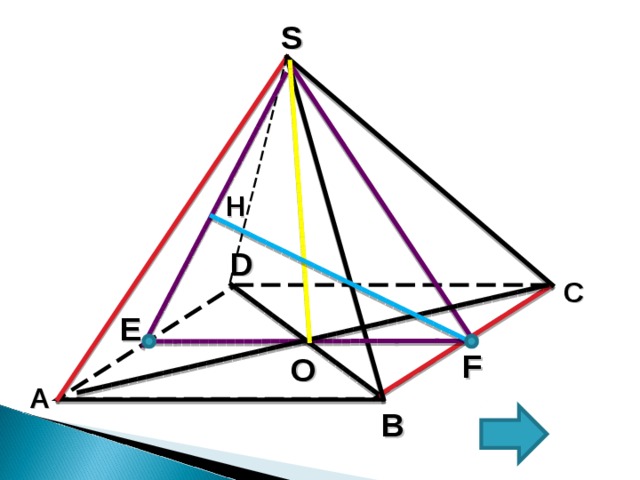
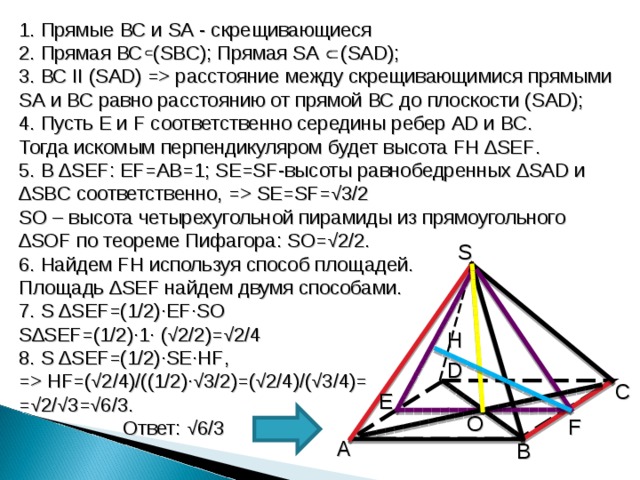
1. Прямые ВС и SA - скрещивающиеся
2. Прямая ВС ( SBC ); Прямая SA ( SAD );
3. ВС II ( SAD ) = расстояние между скрещивающимися прямыми SA и ВС равно расстоянию от прямой ВС до плоскости ( SAD );
4. Пусть E и F соответственно середины ребер AD и BC .
Тогда искомым перпендикуляром будет высота FH ∆ SEF .
5. В ∆ SEF : EF =АВ=1; SE=SF -высоты равнобедренных ∆ SAD и ∆ SBC соответственно, = SE=SF =√3/2
SO – высота четырехугольной пирамиды из прямоугольного ∆ SOF по теореме Пифагора: SO =√2/2.
6. Найдем FH используя способ площадей.
Площадь ∆ SEF найдем двумя способами.
7. S ∆ SEF=(1/2)∙EF∙SO
S ∆ SEF=(1/2)∙1∙ ( √ 2/2)=√2/4
8. S ∆ SEF=(1/2)∙SE∙HF ,
= HF=(√2/4)/((1/2)∙√3/2)=(√2/4)/(√3/4)=
= √2/√3=√6/3 .
Ответ: √6/3
S
H
D
C
E
O
F
А
B
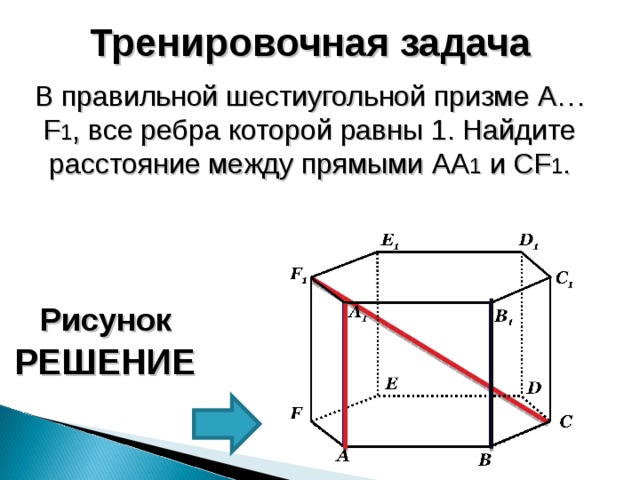
Тренировочная задача
В правильной шестиугольной призме A…F 1 , все ребра которой равны 1. Найдите расстояние между прямыми AA 1 и CF 1 .
Рисунок
РЕШЕНИЕ
M
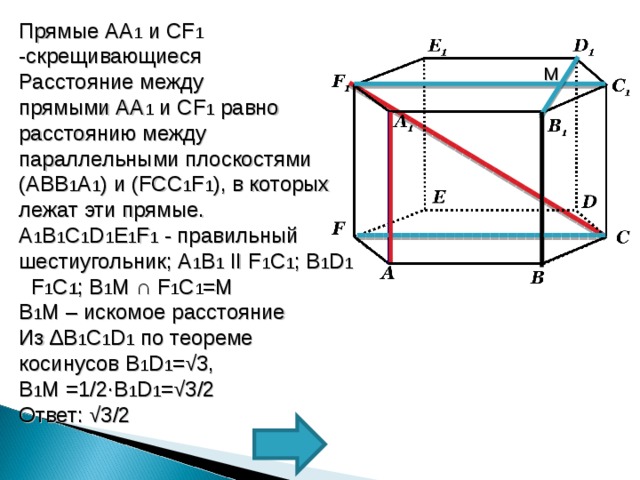
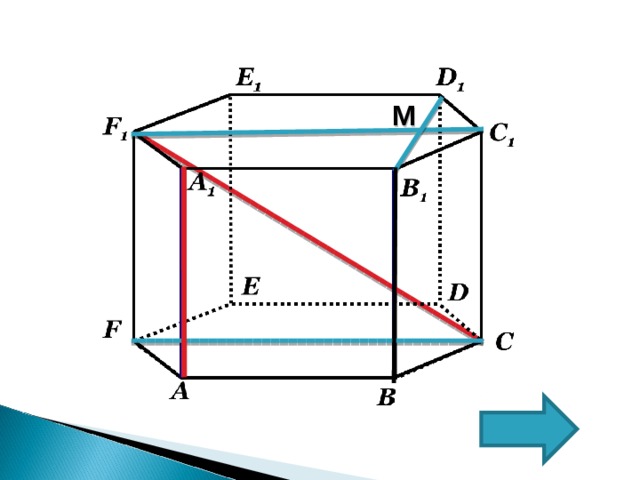
Прямые АА 1 и СF 1 -скрещивающиеся
Расстояние между
прямыми АА 1 и СF 1 равно
расстоянию между
параллельными плоскостями (АВВ 1 А 1 ) и (FCC 1 F 1 ), в которых
лежат эти прямые.
A 1 B 1 C 1 D 1 E 1 F 1 - правильный шестиугольник; A 1 B 1 II F 1 C 1 ; B 1 D 1 F 1 C 1 ; B 1 M ∩ F 1 C 1 =M
B 1 M – искомое расстояние
Из ∆ B 1 C 1 D 1 по теореме косинусов B 1 D 1 =√3,
B 1 M =1/2∙B 1 D 1 =√3/2
Ответ: √3/2
M







