Разработка урока в 9 классе по теме «Последовательности»

Разработка урока в 9 классе по теме «Последовательности»

Цели урока: создание условий для:

• формирования понятия числовой последовательности и способов её задания, для формирования опыта смыслотворчества;

• развитие способности к обобщению, сравнению; эмоционального восприятия математических объектов;

• формирование представлений о математике как способе познания, сохранения и гармоничного развития мира, как части общечеловеческой культуры.

Планируемые результаты:

• личностные:

• умение понимать смысл поставленной задачи, ясно и чётко излагать свои мысли в устной речи, выстраивать аргументацию, приводить контрпримеры;

• опыт смыслообразования;

• самооценка результатов деятельности, осознание границ применения нового знания;

• умение работать в команде;

• ценностно-эмоциональное отношение к изучаемому математическому содержанию с общекультурных позиций;

• представление о значении математической науки как сфере человеческой деятельности;

• метапредметные:

• умение выделять главное, сравнивать, обобщать, проводить аналогию, применять индуктивные способы рассуждений, выдвигать гипотезы при решении учебных задач;

• осознанное чтение текста;

• способность к интерпретации;

• представление о математике как средстве моделирования явлений окружающего мира;

• предметные:

• понятие числовой последовательности;

• умение использовать индексные обозначения и строить речевые высказывания с использованием специальной терминологии ( а_п ; а_п-1; а_п+1 и т.п.);

• умение устанавливать закономерность в построении последовательности, если выписаны первые несколько её новых членов;

• умение изображать члены последовательности точками на координатной плоскости;

• использовать различные языки математики (словесный – символический – графический).

Ход урока

I этап. Актуализация знаний учащихся

1.1. Учитель. Сегодня мы приступаем к изучению новой для вас темы. Эта тема может быть «пройдена» вами, а может быть «прожита». Надеюсь, что сегодняшний урок, выводя вас на смыслы изучаемых понятий, поможет освоить новую тему с интересом и хорошими результатами, одним из которых будет яркий образ науки математики как способе познания, сохранения и гармоничного развития мира.

Одним из основных понятий, изучением которых занимается математика, является понятие числа. Мир чисел таит столько загадок и тайн! В то же время язык чисел близок и интересен многим людям, даже довольно далёким от математики. Наверное, поэтому числовые головоломки решают и взрослые, и дети. Я предлагаю вам несколько таких головоломок, взятых мною из сети Интернет. Думаю, их разгадывание позволит не только провести интеллектуальную разминку в начале урока, но и выведет вас на дорогу познания смыслов новых математических понятий, связанных с его величеством Числом.

1.2. Самостоятельная работа (индивидуально, с разрешением работать в парах).

Задание 1. Вставьте промежуточные числа, если все тройки чисел составлены по одному и тому же правилу:

а) б) в)

Задание 2. Найдите закономерность в последовательности чисел и замените вопросительный знак числом:

Задание 2. Найдите закономерность в последовательности чисел и замените вопросительный знак числом:

82, 97, 114, 133, ? .

Проверка выполнения (фронтально): ученики называют полученные ответы, объясняя, какую закономерность они установили.

Комментарий. При обсуждении решений следует поощрять разные способы нахождения закономерностей. Таким образом, вариантов ответов в каждом случае может быть несколько.

1.3. Беседа с элементами дискуссии.

Вопрос. Можно ли поставить другое число вместо числа 6 в случае 1а)? вместо числа 14 в случае 1б)?

Предполагаемый ответ: Да, если мы найдём иную закономерность между числами 8, 5 и 3 помимо 8 – 5 = 3 (или для второго случая одинаковую закономерность для троек чисел 2, 4, 10 и 3, 5, 17).

Комментарий. В случае положительного ответа ученики могут показать, например, следующий вариант: 5+8=13, количество единиц 3. Тогда 13+7=20, количество единиц 0, это и будет искомым числом.

В случае отрицательного ответа можно обойтись и очевидными закономерностями, тем более если учащиеся не нашли при работе с головоломками иных вариантов решения, и сэкономить на этом время обсуждения. Но почему бы не использовать возможности этого задания для развития критичности и вариативности мышления?

Вопрос. Как вы понимаете слово «закономерность»?

(Очевидно, что в ходе обсуждения учащиеся будут оперировать понятиями, известными им из курса обществознания: правило – закон – норма – право.)

Учитель. Верно, однокоренные слова закономерность и закон – это близкие понятия. Убедимся в этом с помощью философского словаря.

Комментарий. На слайде выводится определение: Философский словарь: «Закон – внутренняя существенная и устойчивая связь явлений, обусловливающая их упорядоченные изменения. На основе знания закона возможно достоверное предвидение течения процесса. Понятие «закон» близко к понятию закономерность, которое представляет собой совокупность взаимосвязанных законов, обеспечивающих устойчивую тенденцию или направленность в изменениях системы».

Вопрос. Каковы, на ваш взгляд, главные слова в этом определении?

Комментарий. Хорошо, если слова, называемые учащимися, выделяются на слайде по ходу обсуждения

Вопрос. Как вы думаете, возможно ли существование мира без законов?

Предполагаемый ответ: Законы природы и естественные законы (механические, физико-химические, органические законы и др.) существуют объективно и не зависят от желаний людей: закон всемирного тяготения, законы электричества, генетики и т.п. Законы же, придуманные людьми, носят субъективный характер, отражают интересы отдельных групп людей, соблюдаются или не соблюдаются.

Вопрос. А лично вам нужны законы?

Предполагаемый ответ: Знание законов позволяет защитить себя в как в природе, так и в обществе. Освоение человеком норм равносильно приобретению им различных прав. Право – норма свободы. Изучая законы, человек определяет своё место в мире и познаёт себя.

Вопрос. Нужно ли изучать законы?

Предполагаемый ответ: Познать закон означает раскрыть ту или иную сторону сущности исследуемого предмета, явления. На протяжении тысячелетий познание законов природы способствовало развитию человеческой цивилизации. Познание законов человеческого общества нужно для предотвращения социальных конфликтов и устойчивого развития общества. Законы позволяют прогнозировать развитие событий, явлений.

Вопрос. Какую роль математика играет в познании человеком законов мира?

Предполагаемый ответ: Математика является верным союзником человека на пути познания законов природы и человеческого общества: она и инструмент моделирования реальных объектов и явлений, и универсальный язык науки и техники. И наоборот, идеи математики способствуют развитию всех наук, экономики, человеческого общества.

II этап. Освоение нового материала

2.1. Учитель. Отражая существенные и устойчивые связи явлений реального мира, математика и сама соткана из законов и закономерностей. Многие закономерности, существующие в мире чисел, были известны ещё в древности

2.2. Работа в микрогруппах.

Задание 3. Попробуйте по первым числам из серий чисел догадаться, по какому правилу построены эти серии:

1. 1, 2, 3, 4,…

2. 2, 4, 6, 8, …

3. 1, 3, 5, 7, …

4. 1, 4, 9, 16, …

5. 2, 3, 5, 7, 11, …

6. 1, , , , …

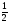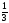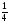Проверка выполнения: устное представление каждой микрогруппой результатов выполнения задания.

Предполагаемый ответ:

1) 1, 2, 3, 4, 5, 6, … - натуральные числа;

2) 2, 4, 6, 8,10, … - чётные числа;

3) 1, 3, 5, 7, 9, … - нечётные числа;

4) 1, 4, 9, 16, 25, 36, … - квадраты натуральных чисел;

5) 2, 3, 5, 7, 11, 13, 17, … - простые числа;

6) 1, 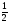, , 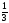, , 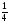,…- числа, обратные натуральным.

Комментарий: По ходу обсуждения на слайде появляются следующие члены последовательностей и названия этих числовых множеств.

Задание 4. Попробуйте определить, что является общим и главным для всех этих серий чисел.

Проверка выполнения: устное представление каждой микрогруппой своих гипотез.

Предполагаемый ответ: Общим для всех рядов чисел является то, что числа записаны в определённом порядке, последовательности.

Комментарий: Предоставляется хорошая возможность для развития умений слушать друг друга, выстраивать аргументацию, приводить контрпримеры (например, кто-то выскажет мысль о возрастании чисел в каждом из рядов – в этом случае шестой пример будет хорошим контрпримером). В ходе обсуждения должны появиться следующие слова: очерёдность, порядок и т.п.

Задание 5. Попробуйте сформулировать определение понятия «числовая последовательность».

Проверка выполнения: каждая микрогруппа представляет свою формулировку определения.

Комментарий. Это можно сделать на доске, на заранее заготовленных листах формата А3 или выведением на слайд.

Учитель. Сравните своё определение с определением из школьного учебника: «Записанные в определённом порядке числа называются числовыми последовательностями».

2.3. Фронтальная работа.

Учитель. В общем случае числовые последовательности могут быть конечными и составлены из произвольных чисел. Числовыми последовательностями, например, являются выписанные по порядку отметки каждого из вас в классном журнале по алгебре или результаты каких-либо измерений: например, температуры воздуха. Главным является именно порядок: каждое число стоит на своём месте. Запишем числовую последовательность в общем виде.

На 1 месте а₁

на 2 месте а₂

на 3 месте а₃

Все числа последовательности называются членами последовательности, индексы 1, 2, 3, … - номерами членов

последовательности.

Вопросы:

– Как записать член последовательности с номером 4?

– С номером п?

– Какой номер будет у члена последовательности, предшествующего а_п?

– А у следующего за ним?

– Как записать член последовательности, предшествующий а_п?

– Следующий за ним?

Комментарий: Хорошо, если будет задействована анимация: на этом же слайде одновременно с каждой строчкой появляется каждый следующий член последовательности в записи

а₁, а₂, а₃, …, а_п-1, а_п, а_п+1, … - числовая последовательность, коротко: (а_п) или в некоторых учебниках:

На 1 месте а₁

на 2 месте а₂

на 3 месте а₃

……………………….

на п-1-вом месте ….

на п-ном месте …

на п+1-вом месте …

……………………….

2.4. Работа в микрогруппах.

Учитель. Очевидно, что номера – это натуральные числа. Таким образом, числовая последовательность представляет собой функцию натурального аргумента: а_п=f(п).

Задание 6. Вы умеете строить графики многих элементарных функций, изучаемых в школьном курсе математики. Используя этот опыт, изобразите точками на координатной плоскости несколько первых членов числовой последовательности (любой из шести, с которыми мы уже работали или вами придуманной). Давайте уточним:

- что будем откладывать по горизонтальной оси?

- по вертикальной?

Проверка выполнения: представление каждой микрогруппой графика выбранной последовательности.

Комментарии. 1. Для организации такой работы нужно заранее приготовить листы формата А3 с заранее нанесённой на них системой координат.

2. Выполнение этого задания позволяет наглядно обеспечить понимание того факта, что последовательность - это зависимость, функция натурального аргумента. Сопоставление разных графиков пригодится учащимся при изучении прогрессий для сравнения свойств арифметической и геометрической прогрессий.

3. Есть смысл показать график не монотонной последовательности, например, такой: 0, 1, , , ,….(*) (Первый член равен 0, второй – 1, каждый, начиная с третьего, равен полусумме двух предыдущих).

Если нечто похожее придумают сами учащиеся, этот пример можно не использовать.

2.5. Фронтальная работа.

Задание 7. Итак, там, где каждому натуральному п соответствует своё число а_п, мы говорим о числовой последовательности. Приведите свои примеры числовых последовательностей.

Проверка выполнения: по желанию учащиеся представляют придуманные ими последовательности у доски.

Вопрос: В чём была трудность выполнения задания?

Предполагаемый ответ: Трудно было придумать связь между членами последовательности (правило или закономерность для составления последовательности).

Учитель. Вот мы и опять вернулись к понятию «закономерность». Слово закономерность состоит из двух корней: закон и мера, значит, закономерность предполагает возможность измерить что-то неким законом. В нашем случае: постичь взаимосвязь между числами-членами последовательности.

Вопрос. А как соотносятся с изучаемой нами темой наши рассуждения о необходимости знать закон?

Предполагаемый ответ: Если установить, по какому закону установлена взаимосвязь между членами последовательности, можно определить любой член последовательности.

2.6. Работа в микрогруппах.

Учитель. Существует три способа задания числовых последовательностей.

1-й способ. Самый удобный, когда по номеру можно вычислить соответствующий член последовательности.

Задание 8. Попробуйте для вышеперечисленных последовательностей связать в формулу переменные п и а_п.

Проверка выполнения: Каждая микрогруппа представляет результаты деятельности у доски.

Комментарии: 1. Следует отметить, что учащиеся знакомы с формулами чётного и нечётного числа, им под силу составить формулы и для других случаев.

2. По завершении отчётов групп формулы п-ного члена последовательностей появляются на уже известном слайде:

1) 1, 2, 3, 4,…(а_п=п) - последовательность натуральных чисел;

2) 2, 4, 6, 8, …(а_п=2п) - последовательность чётных чисел;

3) 1, 3, 5, 7, …(а_п=2п-1) - последовательность нечётных чисел;

4) 1, 4, 9, 16, …(а_п=п²) - последовательность квадратов натуральных чисел;

5) 2, 3, 5, 7, 11, …? - последовательность простых чисел;

6) 1, 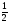, , 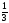,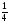…(а_п=) - последовательность чисел, обратных натуральным.

3. Полезно устно убедиться в справедливости формул.

Учитель. Составленные вами формулы называются формулами п–ного (или общего) члена последовательности. Итак, первый способ задания последовательности – формулой п-ного члена.

Вопрос. С какой трудностью вы столкнулись при выполнении задания?

Предполагаемый ответ: Для последовательности 5 нельзя задать формулу n-ного (общего) члена.

Учитель. В таком случае используют описательный способ. Для данной последовательности в III веке до н.э. александрийский учёный Эратосфен указал способ получения п-ного члена. Вспомните знаменитое «решето Эратосфена»! Итак, второй способ – описательный.

Задание 9. а) Попробуйте применить описательный способ задания последовательности из чередующихся нулей и единиц 1, 0 , 1, 0, ….

б) Эту же последовательность можно задать и формулой п-ного члена. Составьте эту формулу.

Проверка выполнения: устное представление результата (описательно: на нечётных местах 1, на чётных 0; аналитически: , где ).

Комментарий. В классе со слабой подготовкой задание 9б можно не предлагать (дать его индивидуально «сильным» учащимся).

Учитель. Третий способ задания последовательности называется рекуррентным (от латинского recursio – возвращаться). Он позволяет, зная один или несколько предыдущих членов, найти следующий член числовой последовательности. Примером, демонстрирующим этот способ, является последовательность (*): в ней а₁=0; а₂=1; каждый следующий член, начиная с предыдущего:

а_п=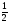(а_п-₂ +а_п-1) .

Каждый способ имеет свои достоинства. На следующих уроках вы сможете их оценить.

2.7. Рассказ учителя. Домашнее задание.

Учитель. С последовательностями связанно много интересных задач, берущих своё начало в практической деятельности человека. Со времён средневековья известна задача о кроликах, которую связывают с именем Леонардо Фибоначчи, итальянского учёного из города Пиза.

Вот один из вариантов этой задачи:

Пара кроликов, начиная с двухмесячного возраста, ежемесячно производит новую пару. Сколько всего пар кроликов будет в декабре, если первая пара новорождённых кроликов появилась в январе (при условии, что все кролики останутся живы)?

Задание 10. К следующему уроку я прошу вас придумать способ решения данной задачи, выписать последовательность чисел, которая получится в ходе решения и попытаться определить, каким способом можно её задать.

Комментарий. Записать домашнее задание:

1) изучить теорию (соответствующие номера пунктов или параграфов);

2) придумать способ решения и решить задачу Фибоначчи; найти способ задания последовательности Фибоначчи.

Кому будет трудно, можете воспользоваться различными энциклопедиями по математике. Информацию вы легко найдёте. Ведь эта последовательность, члены которой называются числами Фибоначчи, широко известна в мире. Вот лишь несколько примеров:

В природе. Расстояния между листьями (или ветками) на стволе растения относятся, примерно, как числа Фибоначчи.

В культуре: Светящиеся числа Фибоначчи от 1 до 55 прикреплены на дымовой трубе Turku Energia в г. Турку.

В интерьерном и ландшафтном дизайне: Ряд Фибоначчи используется для вычисления гармоничных пропорций, например, соотношение высоты помещения к высоте декорирования стен различными материалами или соотношение высот нескольких деревьев в группе.

В литературе: Американский писатель-фантаст Дэн Браун в книге «Код да Винчи» описал последовательность Фибоначчи как «лжешифр».

В стихосложении: Последовательность Фибоначчи была хорошо известна в древней Индии, где она применялась для написания стихотворных произведений, причём значительно раньше, чем она стала известна в Европе.

Учитель. Надеюсь, вам очень хочется увидеть, как выглядит последовательность Фибоначчи. Но оставим эту интригу для домашней работы.

Комментарии. 1. Задача Фибоначчи именно в такой формулировке есть в учебнике Дорофеева Г. В. Тем, кто учится по другим учебникам, можно её напечатать .

2. На слайде: Леонардо Фибоначчи, г. Пиза.

Последовательность Фибоначчи - ?

3. Примеры, иллюстрирующие применение ряда Фибоначчи, можно напечатать на каждую парту или вывести на слайды.

III этап. Рефлексия

3.1. Работа в микрогруппах

Задание 11. Составьте краткий конспект или схему по содержанию изученного сегодня на уроке материала. Главное условие выполнения: лаконичность и содержательность.

Проверка выполнения: Каждая микрогруппа представляет результаты деятельности у доски.

3.2. Беседа

Вопрос. А из тех последовательностей, которые вы рассмотрели сегодня на уроке, какая вам представляется наиболее интересной и чем?

Предполагаемые ответы: Первая последовательность знакома нам с детства, причём мы все учимся считать именно в этой последовательности. Последовательность 6 отличается своей загадочностью: её члены с возрастанием номеров уменьшаются, но никогда, несмотря на бесконечное её убывание, её члены не достигнут нуля и т. п.

Комментарий. На слайде: список последовательностей, с которыми работали на уроке.

Учитель. Конечно же, русское слово «последовательность» было знакомо вам ещё до сегодняшнего урока. Посмотрите, какие синонимы существуют у этого слова:

- логичность, связность, непротиворечивость;

- порядок, очерёдность;

- череда, вереница, цепочка;

- ряд.

Вопросы.

• Какой синоним наиболее отвечает вашему представлению о последовательностях?

• С чем лично у вас ассоциируется понятие последовательности?

• Что вам дало изучение понятия числовой последовательности?

• Что вызвало наибольшие затруднения?

• Каков для вас смысл сегодняшнего урока?

Комментарии. 1. При рефлексии своей деятельности учащиеся должны зафиксировать свои затруднения. Следует обратить их внимание на то, что сформулировать собственные трудности – это уже наполовину с ними справиться. В зависимости от затруднений - дать конкретные рекомендации.

2. В подготовленном классе обсуждение понятия «последовательность» может привести к категориям «порядок» и «хаос», а от них – к категории «гармония». Это позволит выйти на создание учебного проекта «Математика гармонии» с проблемным вопросом «Можно ли измерить красоту?».