Открытый урок по алгебре 9 класс. 12.10.17г. Учитель ПриходькоЛ.М.
Тема: «Построение графика квадратичной функции»
Цели урока:
- знать определение квадратичной функции, алгоритм построения графика квадратичной функции;
- уметь находить координаты вершины параболы, дополнительные точки, строить параболу;
- воспитывать внимательность, самостоятельность, закрепить навыки работы с чертежными принадлежностями, учиться культуре чертежа.
Оборудование: мультимедийный проектор, индивидуальные карточки.
Ход урока.
I. Организационный момент.
На прошлом уроке мы рассмотрели различные преобразования параболы. Посмотрели на множество примеров, научивших нас увидеть красоту этих графиков и в архитектуре, и в природе, и в …
А может вы добавите теперь и свои примеры?
II. Проверка домашнего задания.
Усвоение домашнего задания проверим с помощью групповых заданий и фронтального опроса.
1 группа. Найдите соответствие между графиком функции и ее формулой.
2 и 3 группы. Определить график какой функции изображен на рисунке. Назовите промежутки возрастания и убывания функции.


А. у = (х – 1)2 + 3 Б. у = – (х + 3)2 + 1 В. у = – (х + 3)2 – 1
А. у = (х – 1)2 + 1 Б. у = - (х + 1)2 – 1 В. у = (х – 1)2 – 1
III. Актуализация знаний. ( Фронтальный опрос. Одновременно несколько учащихся работают по индивидуальным карточкам ).
Функция какого вида называется квадратичной?(y = ax2, y = ax2 + n, y = a(x – m)2, y = a(x – m)2 + n).
Что является графиком квадратичной функции? (парабола)
Сколько точек необходимо для построения параболы? (минимум 5)
От чего зависит направление ветвей параболы? (а 0 ветви вверх, a
На что еще влияет коэффициент а?
С помощью какого преобразования можно получить график функции у = 0,5х2 – 2 ?
А какой параллельный перенос поможет построить график функции у = 2(х – 3)2 ?
IV. Изучение нового материала.
Квадратичной функцией называется функция, которую можно задать формулой вида
y = ax² + bx + c, где х - независимая переменная, a, b и с -некоторые числа (причём а≠0).
Графиком квадратичной функции является парабола, ветви которой направлены вверх(если а 0) или вниз (если а
Чтобы построить график функции есть три способа:
1 способ.
Выделить квадрат двучлена из квадратного трехчлена в виде y = a(x – m)2 + n.
Построить график с помощью двух параллельных переносов.
2 способ.
Найти координаты вершины параболы А(m;n) по формулам: m = –
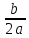 ; n = у(m) т.е. подставить найденное значение абсциссы m в формулу, которой задана функция и вычислить значение.
; n = у(m) т.е. подставить найденное значение абсциссы m в формулу, которой задана функция и вычислить значение.Прямая x=m является осью симметрии параболы.
Заполнить таблицу значений функции: в таблице расположить вершину в середине таблицы и взять соседние симметричные значения х.
Построить график функции: - отметить в координатной плоскости точки, координаты которых указаны в таблице; - соединить их плавной линией.
Построим график функции у = х²-2х-1 по алгоритму
| m = – n=1-2-1=-2 Вершина параболы (1;-2). Прямая х=1 ось симметрии праболы. Ветви параболы направлены вверх, т.к. a = 1, a 0.
|
|
3 способ.
С помощью точек, имеющих ординаты равные коэффициенту с.

V. Физминутка.
1. Повороты головы вправо- влево, вверх- вниз, показываем смещение вершины параболы
у = – х2 + 3, у = – (х – 2)2, у = – х2 + 6
у = х2 – 5, у = (х + 1)2, у = х2 – 8.
2. Движения руками вверх- вниз, показываем направление ветвей параболы.
у = х2 + 3, у = – (х – 2)2 + 2 , у = х 2 – 5,
у = – х 2 + 6, у = (х + 1)2 – 5, у = – х2 – 8.
VI. Решение упражнений.
№ 121 (найти координаты вершины параболы)
№122 (построить график, выяснить свойства функции)
VII. Подведение итогов:
Ответьте на вопросы. Верно ли, что:
Вершина параболы находится по формулам m = –
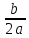 , n = –
, n = – 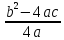
При а 0 ветви параболы направлены …
При а
Как называют точки пересечения параболы с осью Ох?
Домашнее задание: n.7, стр. 46 к.в.1 – 4 , №123, №124.
Рефлексия
стали друзьями, мы стали умнее,
Богаче на целый волшебный урок!
Нас знания делают выше, сильнее,
А дружба крепче и добрей.
Ты согласен, дружок?
На уроке я работал активно / пассивно
Своей работой на уроке я доволен / не доволен
Урок для меня показался коротким / длинным
За урок я не устал / устал
Моё настроение стало лучше / стало хуже
Материал урока мне был понятен / не понятен
Домашнее задание мне кажется лёгким / трудным
Для меня урок был полезен / бесполезен
интересен / скучен



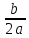 ; n = у(m) т.е. подставить найденное значение абсциссы m в формулу, которой задана функция и вычислить значение.
; n = у(m) т.е. подставить найденное значение абсциссы m в формулу, которой задана функция и вычислить значение. ;
;