Опорные сигналы, как основа системного
подхода на уроках математики
Страшкова Е.А.
Учитель высшей категории
МБОУ «СОШ № 1 им. Созонова Ю.Г.»
г. Ханты-Мансийск
Все дети разные, и каждый из них развивается своим темпом. Вместе с тем обучение в массовой школе сориентировано на некий средний уровень, который слишком высок для слабых детей и явно недостаточен для более сильных. Это тормозит развитие как сильных детей, так и слабых. Чтобы учесть индивидуальные особенности учащихся, часто выделяют 2, 4 и т.д. уровня. Однако реальных уровней в классе ровно столько, сколько детей! Возможно ли их точно определить? Не говоря уже о том, что практически трудно учесть даже четыре — ведь для учителя это означает 20 подготовок в день! Выход прост: выделить всего лишь два уровня — максимум, определяемый зоной ближайшего развития детей, и необходимый минимум. Принцип минимакса заключается в следующем: школа должна предложить ученику содержание образования по максимальному уровню, а ученик обязан усвоить это содержание по минимальному уровню. Система минимакса является, видимо, оптимальной для реализации индивидуального подхода, так как это саморегулирующаяся система. Слабый ученик ограничится минимумом, а сильный — возьмет все и пойдет дальше. Все остальные разместятся в промежутке между этими двумя уровнями в соответствии со своими способностями и возможностями — они сами выберут свой уровень по своему возможному максимуму. Работа ведется на высоком уровне трудности, но оценивается лишь обязательный результат, и успех. Это позволит сформировать у учащихся установку на достижение успеха, а не на уход от “двойки”, что гораздо важнее для развития мотивационной сферы. Принцип психологической комфортности предполагает снятие по возможности всех стрессообразующих факторов учебного процесса, создание в школе и на уроке такой атмосферы, которая расковывает детей и в которой они чувствуют себя “как дома”.
Системный подход преподавания математики рассматривается как совокупность взаимосвязанных элементов. Умение увидеть задачу с разных сторон, проанализировать множество решений, из единого целого выделить составляющие или, наоборот, из разрозненных фактов собрать целостную картину, - будет помогать не только на уроках, но и в обычной жизни. Обучение, реализующее принцип деятельности, называют деятельностным подходом. Еще Я.А. Коменский отмечал, что явления нужно изучать во взаимной связи, а не разрозненно. Естественно, что при этом знания, формируемые у учащихся, должны отражать язык и структуру научного знания. Принцип непрерывности означает преемственность между всеми ступенями обучения на уровне методологии, содержания и методики.
Для реализации всех перечисленных выше принципов хорошо работают на уроках математики опорные сигналы. Собственно с них начинается изучение нового материала по каждой теме. После рассмотренных примеров дети «открывают» в процессе исследовательской деятельности правила, алгоритмы выполнения заданий. Выводы этой исследований формируем в опорные сигналы (ОС). Например, в 5
классе мы получили такой ОС по теме «Округление натуральных чисел»:

Степень участия каждого ученика в начале работы над темой различная: кто-то в силу своих способностей генерирует идею, кто-то – воплощает эти идеи на листе, кто-то формулирует вопросы по данной теме для листа группового взаимоконтроля, кто-то объясняет что изображено по готовому ОС. Ниже привожу примеры ОС при изучении математики в 5 классе. Работа с ОС заканчивается письменным их воспроизведением на следующем уроке и устными ответами по вопросам из листов группового взаимоконтроля.
|
| Вопросы листа группового контроля 1.Назовите компоненты при сложении чисел 2.Какое действие является обратным для сложения? 3.Назовите компоненты при вычитании. 4.Какое число называют корнем уравнения? 5.Что значит решить уравнение? 6.Как найти неизвестное слагаемое. 7.Как найти неизвестное уменьшаемое? 8.Как найти неизвестное вычитаемое? 9.Сформулируйте переместительный закон сложения. Запишите его с помощью. 10.Сформулируйте сочетательные закон сложения. Запишите его с помощью. 11.Перечислите свойства сложения. Запишите их с помощью букв. 12.Перечислите свойства вычитания. Запишите их с помощью букв. 13.Перечислите законы сложения. 14.Сформулируйте переместительный закон. 15.Сформулируйте сочетательный закон сложения. 16.Сформулируйте закон вычитания суммы из числа. 17.Сформулируйте закон вычитания из числа суммы. 18.Сформулируйте правило сложения (вычитания) натуральных чисел.
|
|
| Вопросы листа группового взаимоконтроля 1.Назовите компоненты при умножении. 2.Как найти неизвестный множитель? 3.Какое действие является обратным для умножения? 4.Назовите компоненты при делении. 5.Как найти неизвестный делимое? 6.Как найти неизвестный делитель? 7.Свойства умножения. Запишите его с помощью букв. 8.Перечислите свойства деления чисел. 9.Перечислите законы умножения. 10.Сформулируйте переместительный закон умножения. Запишите его с помощью букв. 11.Сформулируйте сочетательный закон умножения. Запишите его с помощью букв. 12.Сформулируйте распределительный закон умножения. Запишите его с помощью букв. 13.Правило умножения десятичной дроби на 10, на 100, на 1000... 14.Как разделить число на 10, 100, 1000…
|
|
| Вопросы листа взаимоконтроля 1.Что такое формула ? 2.Запишите формулу пути, что означают входящие в нее буквы? 3.Как найти скорость? время? 4.Запишите формулу периметра прямоугольника? 5.Как найти сторону прямоугольника, зная вторую сторону и периметр? 6.Запишите формулу периметра квадрата? 7.Как найти сторону квадрата, зная периметр? 8.Запишите формулу площади прямоугольника? 9.Как найти сторону прямоугольника, зная вторую сторону и площадь? 10.Запишите формулу площади квадрата? 11.Какие фигуры называются равными? 12.Могут ли равные фигуры иметь различные площади? А периметры? 13.Как найти площадь всей фигуры зная площадь ее частей? 14.Назовите единицы измерения площадей. 15.Что такое квадратный метр, квадратный дециметр, квадратный километр? 16.В каких единицах измеряют площадь земельных участков? 17.Что такое гектар? Что такое ар? 18.Объясните почему 1дм²=100 см²=10 000мм², 1км²=1000 000м²?
|
|
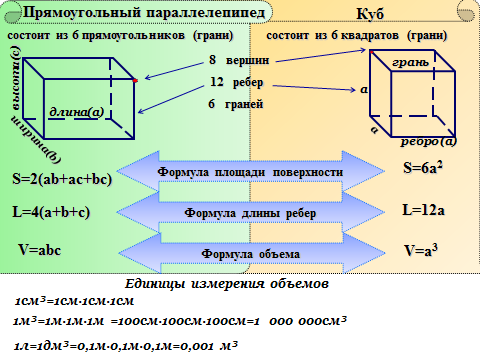
| Вопросы листа взаимоконтроля Приведите примеры предметов, имеющих форму прямоугольного параллелепипеда. Сколько граней имеет прямоугольный параллелепипед. Какую форму имеют грани? Напишете формулу площади поверхности прямоугольного параллелепипеда, куба. Сколько ребер у прямоугольного параллелепипеда. Напишете формулу длин ребер прямоугольного параллелепипеда, куба. Сколько у него вершин? Является ли куб прямоугольным параллелепипедом? Что такое кубический сантиметр? Как еще называют кубический дециметр? Cколько литров в кубическом метре? Напишете формулу объема прямоугольного параллелепипеда. Что обозначают буквы входящие в формулу? Напишете формулу объема куба. |
|
| Вопросы 1.Как называют выражение 2. Как называется число, стоящее над чертой? 3. Как называется число, стоящее под чертой? 4. Что показывает знаменатель? 5. Что показывает числитель? 6. Сколько долей килограммов в 1 грамме? Сколько долей часа в 1 минуте? 7.Как сравнить дроби с одинаковым знаменателем? 8. Какая из точек лежит на координатном луче правее? левее? 9.Как складывают дроби с одинаковым знаменателем? Запишите это правило с помощью букв. 10. Как вычитают дроби с одинаковым знаменателем? Запишите это правило с помощью букв.
|
|
| Вопросы листа взаимоконтроля 1.Какую дробь называют правильной? 2.Правило сравнения двух дробей с одинаковым знаменателем. 3.Правило сравнения двух дробей с одинаковым числителем 4. Какую дробь называют неправильной? 5. Сравните правильную дробь и 1? 6. Сравните неправильную дробь и 1? 7. Сравните неправильную дробь и правильную дробь? 8. Какие дроби можно представить в виде смешанного числа? 9. Как найти целую и дробные части неправильной дроби? 10.Как записать смешанное число в виде неправильной дроби? 11. Правило сложения смешанных чисел. 12. Правило вычитания смешанных чисел.
|
|
| Вопросы листа взаимоконтроля 1.Какие числа называют натуральными? 2. Какая дробь называется обыкновенной? 3. Какая дробь называется десятичной? 4. Какие дроби можно записать в виде десятичной дроби? 6.Сколько цифр после запятой будет стоять в числе 7. Назовите разряды в дробной части десятичной дроби. 8. Прочитайте числа: 3, 72; 152,073, назовите разряды каждого из них. 9. Измениться ли десятичная дробь, если в конце дробной части приписать несколько нулей; отбросить несколько нулей? 10. Как сравнивают десятичные дроби.
|
|
| Вопросы листа группового контроля 1.Назовите компоненты при сложении чисел 2.Какое действие является обратным для сложения? 3.Назовите компоненты при вычитании. 4.Какое число называют корнем уравнения? 5.Что значит решить уравнение? 6.Как найти неизвестное слагаемое. 7.Как найти неизвестное уменьшаемое? 8.Как найти неизвестное вычитаемое? 9.Перечислите законы сложения. 10.Сформулируйте переместительный закон сложения. Запишите его с помощью буквенного выражения. 11.Сформулируйте сочетательные закон сложения. Запишите его с помощью буквенного выражения. 12.Перечислите свойства вычитания для трех чисел. Запишите его с помощью буквенного выражения. 13.Чему равно выражение a+0, a-0, a-a? 14.Сформулируйте правило сложения десятичных дробей. 15.Сформулируйте правило вычитания десятичных дробей.
|
|
| Вопросы листа группового взаимоконтроля 1.Назовите компоненты при умножении. 2.Как найти неизвестный множитель? 3.Перечислите законы умножения. 4.Сформулируйте переместительный закон умножения. Запишите его с помощью букв. 4.Сформулируйте сочетательный закон умножения. Запишите его с помощью букв. 5.Сформулируйте распределительный закон умножения. Запишите его с помощью букв. 6.Свойства умножения. Запишите его с помощью букв. 7.Правило умножения десятичной дроби на 10, на 100, на 1000... 8.Правило умножения десятичной дроби на 0,1, на 0,01, на 0,001.... 9.Правило умножения десятичных дробей.
|
|
| Вопросы листа взаимоконтроля 1.Назовите компоненты при делении. 2. Как найти неизвестный делимое? 3. Как найти неизвестный делитель? 4.Как разделить десятичную дробь на натуральное число? 5. Сформулируйте правило деления на десятичную дробь. 6. Как разделить число на 10, 100, 1000… 7. Как разделить число на 0,1, 0,01, 0,001… 8. Перечислите свойства деления чисел.
|
|
| Вопросы листа группового контроля 1.Что называют процентом? 2.Как перевести проценты в десятичную дробь? 3.Как обратить десятичную дробь в проценты? 4.Как найти 5.Как найти 37% от числа А? 6.Как найти число, 7.Как найти число, 37% которого равны А? 8.Как найти сколько процентов число А составляет от 37? 9.Чему равны 50% от какой-нибудь величины? 25%? 20%? 10%? 150%? 10.Как называют 1% от м? 1% от центнера? 1% рубля?
|