Тема. Линейные неравенства с одной переменной
Цели:
Образовательные: обобщение и систематизации знаний по теме, формирование навыков
решения линейных неравенств с одной переменной.
Развивающие : развитие логического мышления, математической речи, вычислительных
навыков.
Воспитательные: формирование интереса к предмету, воспитание учебной активности,
коллективизма через работу в группах.
Тип урока: урок обобщения и систематизации знаний.
Ресурсы: слайды с заданиями, портреты ученых, карточки «Лото».
Ход урока :
Организационный момент.
Приветствие. Психологический настрой .
Наш урок пройдет под девизом:
«Человек - лишь тогда чего- то добивается,
когда он верит в свои силы»
Андреас Фейербах
Основная часть :
1. Показываю весы с помощью которых взвешиваются два предмета.
- Что я хочу этим сказать?
(Один предмет тяжелее другого этот факт можно записать в виде неравенства)
Неравенство ключевое слово в нашей теме «Линейные неравенства с одной переменной»
- Что можно сравнить в окружающем нас мире?
1. В музыке соотношение звуков по высоте .
2. В географии материки, реки, горы, площади государств.
3. В литературе размеры стихов.
В математике можно сравнить числа и значения выражений.
Сравните значения выражений:
а) x+0,5 и x-(0,2)
б)n:(-8) и n: 8
в) – m : (-4) и – m : 4
г) х-3 и х-8
2. Сравнитеа и в, если
| а) а – в= - 5
| в) в– а= 6
|
| б) а – в= 5 | г) в– а= - 6
|
3. Каков знак а, если известно, что:
а) -6 а 4 а
б) -0,7 аа
2. Деление на 3 группы с помощью портретов ученых Томаса Гарриота, Пьера Бучера, Коши Огюстена Луи. Каждой группе дается сообщение по трем портретам. Группа выбирает сообщение, которое касается их портрета и зачитывает его.
|
Томас Гарриот |
Пьер Бучер |
Коши Огюстен Луи |
| Знаки «больше», «меньше» ввел английский ученый Томас Гарриот (1560-1621). Они появились в его книге «Практика аналитического искусства», изданной посмертно в 1631 году. Эти неравенства называются строгими неравенствами.
| Нестрогие неравенства ( | Французский математик (1789-1857), один из основателей теории функций вывел знаменитое неравенство: Среднее арифметическое чисел больше или равно их среднему геометрическому, при условии, что все числа неотрицательные. |
| Задание. Запишите в виде неравенства, обозначьте неизвестную величину буквой х.
Скорость течения воды в реке меньше 3 км/ч. | Задание.Запишите в виде неравенства, обозначьте неизвестную величину буквой х.
Объем жидкости в сосуде не больше 5 л. | Задание. Запишите в виде двойного неравенства, обозначьте неизвестную величину буквой х.
Градусная мера острого угла больше 00, но меньше 900. |
3. – Числовые промежутки встречаются в различных областях. (Просмотр фильма, в котором учителя истории, географии и литературы говорят о числовых промежутках).
Повторим числовые промежутки с точки зрения математики. (Каждая группа заполняет таблицу и защищает у доски).
| 1 | Изображение промежутка | -5 6 |
|
|
|
| Обозначение
|
| ( -2; 2) |
|
| |
| Название
|
|
|
|
| |
| Неравенство
|
|
| -2 | х |
| 2 | Изображение промежутка |
|
| 15 |
|
| Обозначение
| (2,5; 4) |
|
|
| |
| Название
|
|
|
|
| |
| Неравенство
|
| -3 |
| х |
| 3 | Изображение промежутка |
| -4 6 |
|
|
| Обозначение
| [3.2; 7] |
|
|
| |
| Название
|
|
|
|
| |
| Неравенство
|
|
| -23 | х |
4. Вопросы группам.
1. Дайте определение линейного неравенства с одной переменной.
2. Что называется решением неравенства?
3. Что значит решить неравенство?
4. Назовите алгоритм решения линейного неравенства с одной переменной.
5. Закончите предложения :
1. Если правую часть неравенства поменять местами с его левой ( правой) частью, то …
2. Если к обеим частям числового неравенства прибавить одно и то же число, то…
3. Если обе части числового неравенства умножить или разделить на одно и то же
положительное число, то …
4. Если обе части числового неравенства умножить или разделить на одно и то же
отрицательное число, то…
6. « Карусель»
1гр. 2гр. 3 гр.
5у+9
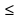 3-7у 1. 9х-310х-14 1. 25-х
3-7у 1. 9х-310х-14 1. 25-х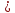 13-3х
13-3х3х+1
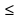 4х-5 2. х-14
4х-5 2. х-14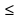 3х-11 2. 12х-16
3х-11 2. 12х-16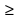 17х+4
17х+46-5у
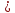 3у-2 3. 5х+205-5х
3у-2 3. 5х+205-5х3-7у
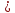 5у-3 4. 10х-12
5у-3 4. 10х-12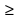 12х-11 4. -2-5х4-4х
12х-11 4. -2-5х4-4хх+3
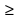 6х-2 5. -3х+123-6х 5. -5х+1
6х-2 5. -3х+123-6х 5. -5х+1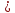 2х+10
2х+103-4у)4-12у 6. -2х+32
7.Игра «Лото». Каждая группа получает карточку с заданиями. Учащиеся сами
распределяют между собой задания.
Решите неравенства:
| 1 | x+2 | 2(x-11) | 6x-5(2x+8)14+2x
|
| 4(x-3) | 4(x-9) |
|
| 2 |
|
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
|
Самостоятельная работа
1 вариант
1.Оцените периметр прямоугольника со сторонами а м и в м, если 3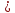 а
а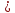 4 и 5
4 и 5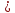 в
в
2.При каких значениях х разность 3( 3х-1) и 2(5х-7) будет положительной
2 вариант
1.Оцените периметр прямоугольника со сторонами х см и у см, если 15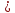 х
х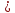 11 и 6
11 и 6
2.При каких значениях х сумма 5(х+4) и 2(-4х+5) будет отрицательной
3 вариант
1.Оцените площадь прямоугольника со сторонами х см и у см, если 15 16 и 20
16 и 20
2.При каких значениях х разность и
меньше или равна 2 .
9.Информация о Д/З
10.Рефлексия : Урок научил меня…
Я понял…
Было трудно…






 ввел французский математик и физик Пьер Бучер (1698-1758). Знаменит ученый тем, что стал первым ученым, определившим количество света, которое теряется при прохождении заданного расстояния в атмосфере.
ввел французский математик и физик Пьер Бучер (1698-1758). Знаменит ученый тем, что стал первым ученым, определившим количество света, которое теряется при прохождении заданного расстояния в атмосфере.
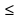





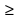 17х+4
17х+4
















