ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
§ 3. Обработка результатов прямого измерения
Для уменьшения влияния случайных ошибок необходимо произвести измерение данной величины несколько раз. Предположим, что мы измеряем некоторую величину x. В результате проведенных измерений мы получили значений величины :
x1, x2, x3, ... xn. (2)
Этот ряд значений величины x получил название выборки. Имея такую выборку, мы можем дать оценку результата измерений. Величину, которая будет являться такой оценкой, мы обозначим ![]() . Но так как это значение оценки результатов измерений не будет представлять собой истинного значения измеряемой величины, необходимо оценить его ошибку. Предположим, что мы сумеем определить оценку ошибки Δx . В таком случае мы можем записать результат измерений в виде
. Но так как это значение оценки результатов измерений не будет представлять собой истинного значения измеряемой величины, необходимо оценить его ошибку. Предположим, что мы сумеем определить оценку ошибки Δx . В таком случае мы можем записать результат измерений в виде
µ = ![]() ± Δx (3)
± Δx (3)
Так как оценочные значения результата измерений ![]() и ошибки Δx не являются точными, запись (3) результата измерений должна сопровождаться указанием его надежности P. Под надежностью или доверительной вероятностью (сенімгерлік межелдемесі) понимают вероятность того, что истинное значение измеряемой величины заключено в интервале, указанном записью (3). Сам этот интервал называется доверительным интервалом.
и ошибки Δx не являются точными, запись (3) результата измерений должна сопровождаться указанием его надежности P. Под надежностью или доверительной вероятностью (сенімгерлік межелдемесі) понимают вероятность того, что истинное значение измеряемой величины заключено в интервале, указанном записью (3). Сам этот интервал называется доверительным интервалом.
Например, измеряя длину некоторого отрезка, окончательный результат мы записали в виде
l = (8.34 ± 0.02) мм, (P = 0.95)
Это означает, что из 100 шансов – 95 за то, что истинное значение длины отрезка заключается в интервале от 8.32 до 8.36 мм .
Таким образом, задача заключается в том, чтобы, имея выборку (2), найти оценку результата измерений ![]() , его ошибку Δx и надежность P.
, его ошибку Δx и надежность P.
Эта задача может быть решена с помощью теории вероятностей (ЫҚТИМАЛДЫЛЫҚ ТЕОРИЯСЫ) и математической статистики.
В большинстве случаев случайные ошибки подчиняются нормальному закону распределения, установленного Гауссом. Нормальный закон распределения ошибок выражается формулой
![]() (4)
(4)
где Δx – отклонение от величины истинного значения;
σ – истинная среднеквадратичная ошибка;
σ 2– дисперсия, величина которой характеризует разброс случайных величин.

Рис.16
Как видно из (4) функция имеет максимальное значение при x = 0 , кроме того, она является четной.
На рис.16 показан график этой функции. Смысл функции (4) заключается в том, что площадь фигуры, заключенной между кривой, осью Δx и двумя ординатами из точек Δx1 и Δx2 (заштрихованная площадь на рис.16) численно равна вероятности, с которой любой отсчет попадет в интервал (Δx1,Δx2) .
Поскольку кривая распределена симметрично относительно оси ординат, можно утверждать, что равные по величине, но противоположные по знаку ошибки равновероятны. А это дает возможность в качестве оценки результатов измерений взять среднее значение всех элементов выборки (2)
 , (5)
, (5)
где – n число измерений.
Итак, если в одних и тех же условиях проделано n измерений, то наиболее вероятным значением измеряемой величины будет ее среднее значение (арифметическое). Величина ![]() стремится к истинному значению μ измеряемой величины при n → ∞.
стремится к истинному значению μ измеряемой величины при n → ∞.
Средней квадратичной ошибкой (орташа квадраттық ауытқу) отдельного результата измерения называется величина
 . (6)
. (6)
Она характеризует ошибку каждого отдельного измерения. При n → ∞ S стремится к постоянному пределу σ
σ = lim S. (7)
n → ∞
С увеличением σ увеличивается разброс отсчетов, т.е. становится ниже точность измерений.
Среднеквадратичной ошибкой среднего арифметического называется величина
 . (8)
. (8)
Это фундаментальный закон возрастания точности при росте числа измерений.
Ошибка ![]() характеризует точность, с которой получено среднее значение измеренной величины
характеризует точность, с которой получено среднее значение измеренной величины ![]() . Результат записывается в виде:
. Результат записывается в виде:
![]() , (9)
, (9)
Эта методика расчета ошибок дает хорошие результаты (с надежностью 0.68) только в том случае, когда одна и та же величина измерялась не менее 30 – 50 раз.
В 1908 году Стьюдент показал, что статистических подход справедлив и при малом числе измерений. Распределение Стьюдента при числе измерений n → ∞ переходит в распределение Гаусса, а при малом числе отличается от него.
Для расчета абсолютной ошибки при малом количестве измерений вводится специальный коэффициент, зависящий от надежности P и числа измерений n, называемый коэффициентом
Стьюдента t.
Опуская теоретические обоснования его введения, заметим, что
Δx = ![]() · t. (10)
· t. (10)
где Δx – абсолютная ошибка для данной доверительной вероятности;![]() – среднеквадратичная ошибка среднего арифметического.
– среднеквадратичная ошибка среднего арифметического.
Коэффициенты Стьюдента приведены в таблице 2.
Из сказанного следует:
Величина среднеквадратичной ошибки позволяет вычислить вероятность попадания истинного значения измеряемой величины в любой интервал вблизи среднего арифметического.
При n → ∞
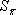 → 0, т.е. интервал, в котором с заданной вероятностью находится истинное значение μ, стремится к нулю с увеличением числа измерений. Казалось бы, увеличивая n, можно получить результат с любой степенью точности. Однако точность существенно увеличивается лишь до тех пор, пока случайная ошибка не станет сравнимой с систематической. Дальнейшее увеличение числа измерений нецелесообразно, т.к. конечная точность результата будет зависеть только от систематической ошибки. Зная величину систематической ошибки, нетрудно задаться допустимой величиной случайной ошибки, взяв ее, например, равной 10% от систематической. Задавая для выбранного таким образом доверительного интервала определенное значение P (например, P = 0.95), нетрудно нейти необходимое число измерений, гарантирующее малое влияние случайной ошибки на точность результата.
→ 0, т.е. интервал, в котором с заданной вероятностью находится истинное значение μ, стремится к нулю с увеличением числа измерений. Казалось бы, увеличивая n, можно получить результат с любой степенью точности. Однако точность существенно увеличивается лишь до тех пор, пока случайная ошибка не станет сравнимой с систематической. Дальнейшее увеличение числа измерений нецелесообразно, т.к. конечная точность результата будет зависеть только от систематической ошибки. Зная величину систематической ошибки, нетрудно задаться допустимой величиной случайной ошибки, взяв ее, например, равной 10% от систематической. Задавая для выбранного таким образом доверительного интервала определенное значение P (например, P = 0.95), нетрудно нейти необходимое число измерений, гарантирующее малое влияние случайной ошибки на точность результата.
Для этого удобнее воспользоваться таблицей 3, в которой интервалы заданы в долях величины σ, являющейся мерой точности данного опыта по отношению к случайным ошибкам.
Таблица 2
| Коэффициенты Стьюдента | |||||
| n | Значения Р | ||||
| 0.6 | 0.8 | 0.95 | 0.99 | 0.999 | |
| 2 | 1.376 | 3.078 | 12.706 | 63.657 | 636.61 |
| 3 | 1.061 | 1.886 | 4.303 | 9.925 | 31.598 |
| 4 | 0.978 | 1.638 | 3.182 | 5.841 | 12.941 |
| 5 | 0.941 | 1.533 | 2.776 | 4.604 | 8.610 |
| 6 | 0.920 | 1.476 | 2.571 | 4.032 | 6.859 |
| 7 | 0.906 | 1.440 | 2.447 | 3.707 | 5.959 |
| 8 | 0.896 | 1.415 | 2.365 | 3.499 | 5.405 |
| 9 | 0.889 | 1.397 | 2.306 | 3.355 | 5.041 |
| 10 | 0.883 | 1.383 | 2.262 | 3.250 | 4.781 |
| 11 | 0.879 | 1.372 | 2.228 | 3.169 | 4.587 |
| 12 | 0.876 | 1.363 | 2.201 | 3.106 | 4.437 |
| 13 | 0.873 | 1.356 | 2.179 | 3.055 | 4.318 |
| 14 | 0.870 | 1.350 | 2.160 | 3.012 | 4.221 |
| 15 | 0.868 | 1.345 | 2.145 | 2.977 | 4.140 |
| 16 | 0.866 | 1.341 | 2.131 | 2.947 | 4.073 |
| 17 | 0.865 | 1.337 | 2.120 | 2.921 | 4.015 |
| 18 | 0.863 | 1.333 | 2.110 | 2.898 | 3.965 |
| 19 | 0.862 | 1.330 | 2.101 | 2.878 | 3.922 |
| 20 | 0.861 | 1.328 | 2.093 | 2.861 | 3.883 |
| 21 | 0.860 | 1.325 | 2.086 | 2.845 | 3.850 |
| 22 | 0.859 | 1.323 | 2.080 | 2.831 | 3.819 |
| 23 | 0.858 | 1.321 | 2.074 | 2.819 | 3.792 |
| 24 | 0.858 | 1.319 | 2.069 | 2.807 | 3.767 |
| 25 | 0.857 | 1.318 | 2.064 | 2.797 | 3.745 |
| 26 | 0.856 | 1.316 | 2.060 | 2.787 | 3.725 |
| 27 | 0.856 | 1.315 | 2.056 | 2.779 | 3.707 |
| 28 | 0.855 | 1.314 | 2.052 | 2.771 | 3.690 |
| 29 | 0.855 | 1.313 | 2.048 | 2.763 | 3.674 |
| 30 | 0.854 | 1.311 | 2.045 | 2.756 | 3.659 |
| 31 | 0.854 | 1.310 | 2.042 | 2.750 | 3.646 |
| 40 | 0.851 | 1.303 | 2.021 | 2.704 | 3.551 |
| 60 | 0.848 | 1.296 | 2.000 | 2.660 | 3.460 |
| 120 | 0.845 | 1.289 | 1.980 | 2.617 | 3.373 |
| ∞ | 0.842 | 1.282 | 1.960 | 2.576 | 3.291 |
Таблица 3
| Необходимое число измерений для получения ошибки Δ с надежностью Р | ||||||
| Δ = Δx/σ | Значения Р | |||||
| 0.5 | 0.7 | 0.9 | 0.95 | 0.99 | 0.999 | |
| 1.0 | 2 | 3 | 5 | 7 | 11 | 17 |
| 0.5 | 3 | 6 | 13 | 18 | 31 | 50 |
| 0.4 | 4 | 8 | 19 | 27 | 46 | 74 |
| 0.3 | 6 | 13 | 32 | 46 | 78 | 127 |
| 0.2 | 13 | 29 | 70 | 99 | 171 | 277 |
| 0.1 | 47 | 169 | 273 | 387 | 668 | 1089 |
При обработке результатов прямых измерений предлагается следующий порядок операций:
Результат каждого измерения запишите в таблицу.
Вычислите среднее значение из n измерений
![]() = Σ x i / n.
= Σ x i / n.
Найдите погрешность отдельного измерения
![]() .
.
Вычислите квадраты погрешностей отдельных измерений
(Δx 1)2, (Δx 2)2, ... , (Δx n)2.
Определите среднеквадратичную ошибку среднего арифметического

Задайте значение надежности (обычно берут P = 0.95).
Определите коэффициент Стьюдента t для заданной надежности P и числа произведенных измерений n.
Найдите доверительный интервал (погрешность измерения)
Δx = ![]() · t.
· t.
Если величина погрешности результата измерения Δx окажется сравнимой с величиной погрешности прибора δ , то в качестве границы доверительного интервала возьмите
![]() .
.
Если одна из ошибок меньше другой в три или более раз, то меньшую отбросьте.
Окончательный результат запишите в виде
![]() .
.
Оцените относительную погрешность результата измерений
![]() .
.
Рассмотрим на числовом примере применение приведенных выше формул.
Пример. Измерялся микрометром диаметр d стержня (БІЛІК) (систематическая ошибка измерения равна 0.005 мм ). Результаты измерений заносим во вторую графу таблицы, находим ![]() и в третью графу этой таблицы записываем разности
и в третью графу этой таблицы записываем разности ![]() , а в четвертую – их квадраты (таблица 4).
, а в четвертую – их квадраты (таблица 4).
Таблица 4
| n | d, мм |
|
|
| 1 | 4.02 | + 0.01 | 0.0001 |
| 2 | 3.98 | - 0.03 | 0.0009 |
| 3 | 3.97 | - 0.04 | 0.0016 |
| 4 | 4.01 | + 0 .00 | 0.0000 |
| 5 | 4.05 | + 0.04 | 0.0016 |
| 6 | 4.03 | + 0.02 | 0.0004 |
| Σ | 24.06 | – | 0.0046 |
![]()
![]()
Задавшись надежностью P = 0.95, по таблице коэффициентов Стьюдента для шести измерений найдем t = 2.57. Абсолютная ошибка найдется по формуле (10).
Δd = 0.01238 · 2.57 = 0.04 мм.
Сравним случайную и систематическую ошибки:
![]() ,
,
следовательно, δ = 0.005 мм можно отбросить.
Окончательный результат запишем в виде
d = (4.01 ± 0.04) мм при Р = 0.95.
![]()







