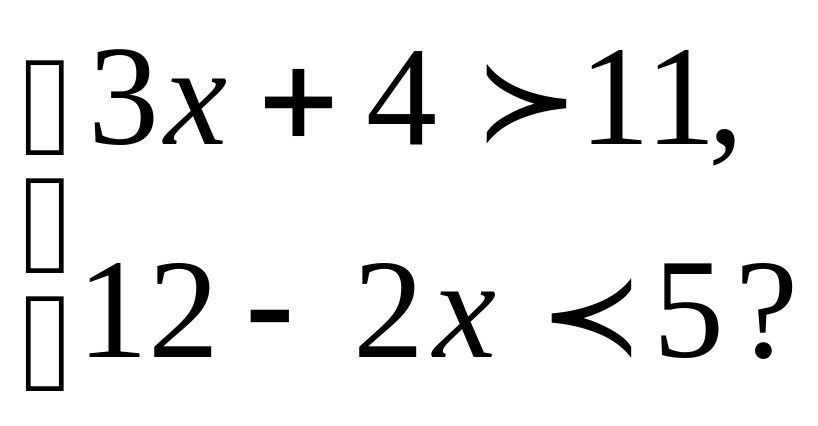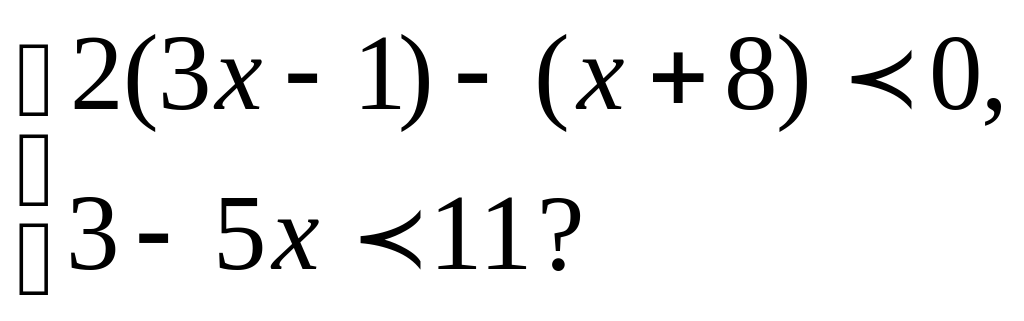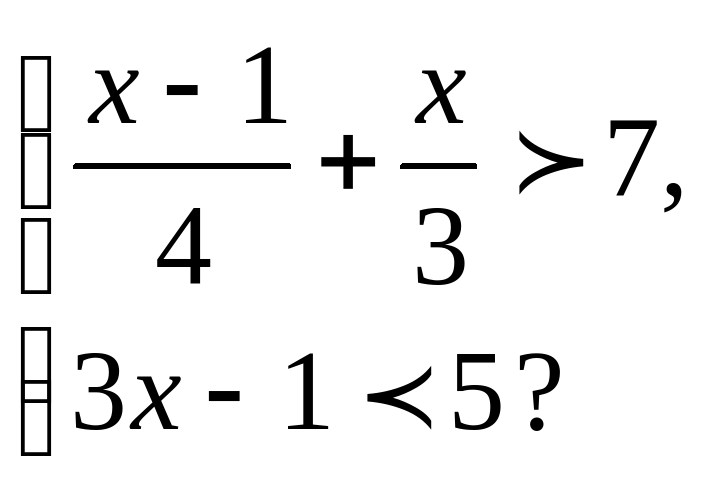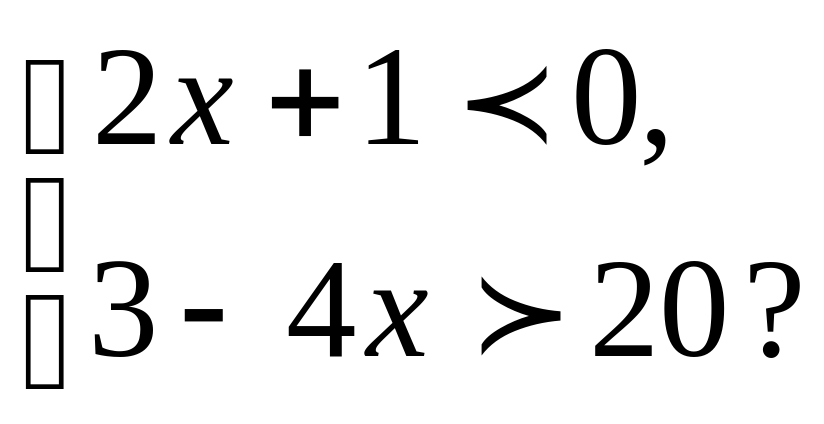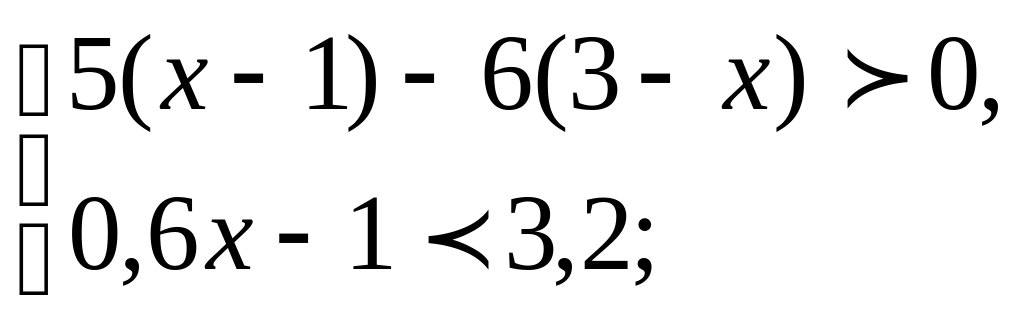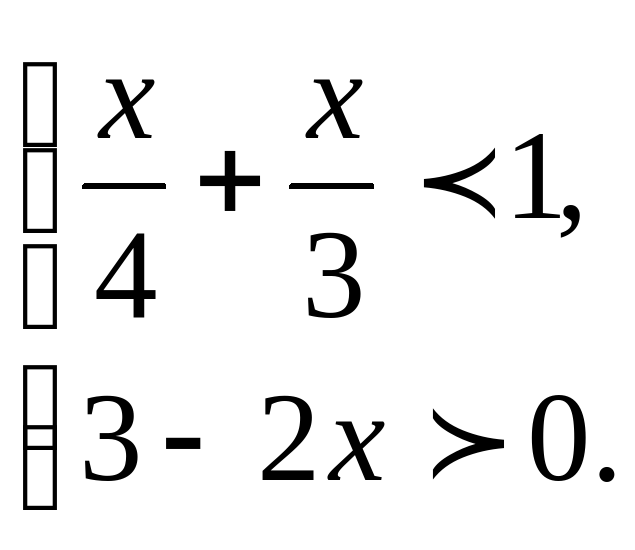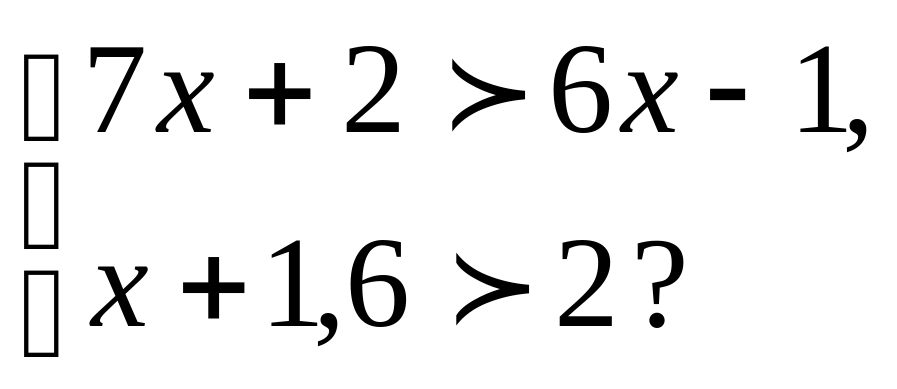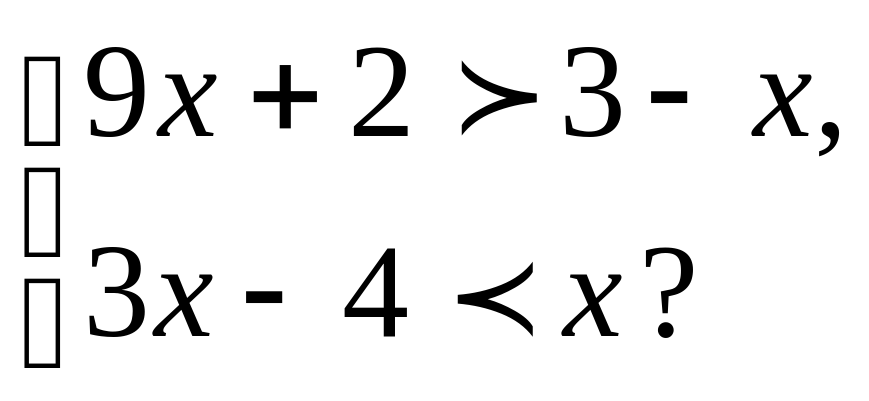Карточки и тесты по алгебре в 9 классе

Данная разработка поможет учителям математики при проведении уроков обобщающего повторения по алгебре в 9 классе.

Олимпиады: Химия 7 - 11 классы

Содержимое разработки

Кондратова Лилия Николаевна.

Учитель математики

МОУ СОШ№4 г. Всеволожск

9 КЛАСС.

ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ.

Последовательность задана формулой п-го члена. Вычислите первые пять членов последовательности

1. а_п=4п-6; 2. а_п=п²-п²; 3. а_п=п ; 4. а_п=0,1^п-1;

5. а_п=1- ; 6. а_п=16-5п; 7. а_п=16-5п ; 8. а_п= п; 9. а_п=-2^п; 10. а_п= .

Последовательность задана рекуррентно формулой. Вычислить первые пять членов последовательности

1. а_п+1=(2п-1) а_п. а₁=2. 2. а_п+1=а_п², а₁=2.

3. а_п+1=3а_п-4, а₁=4. 4. а_п+1=3а_п-1, а₁=3.

5. а_п+1=(2п-2) а_п. а₁=3. 6. а_п+1=а_п-1, а₁=5.

7. а_п+1=0,1 а_п+10. а₁=9. 8. а_п+1=9-2а_п, а₁=-3

9. а_п+1=(-1)^п а_п-8. а₁=5. 10. а_п+1=а_п,! а₁=1.

Чему равны первый член и разность следующих арифметических прогрессий:

1. 6,8,10,…; 2. 25,21,17,…; 3. 4,4 ,4 ,…;

4. 1,1+ ,1+2 ,…; 5. , -3, -6,…; 6. 7,7,7,…; 7. –1,7,-0,9,-0,1,…; 8. 7,9,11,…;

9. –12,-9,-6,…; 10. 3 ,3,2 ,… .

Дана арифметическая последовательность. Вычислите:

1. а₁₅ , если а₁=2, d=3: 2. а₂₀ , если а₁=3, d=4:

3. а₁₅ , если а₁=2, d=3: 4. а₁₈ , если а₁=-3,d=-2:

5. а₁₁ , если а₁=-2,d=-4: 6. а₅ , если а₁=6,d= :

7. а₁₀ , если а₁=4,d=2: 8. а₁₂ , если а₁= -1,d=4:

9. а₂₀ , если а₁= -5,d=2: 10. а₄ , если а₁=2,d=3.

Найти сумму п первых членов арифметической прогрессии, если…

1. а₁=1, а_п=20, п=50; 2. а₁=1, а_п=200, п=100;

3. а₁=-1, а_п=-40, п=20; 4. а₁=2, а_п=100, п=50;

5. а₁=-2, а_п=-60, п=10; 6. а₁=0,5, а_п=25,5, п=11;

7.а₁=1+ ,а_п=1-11 , п=10 8. а₁= ,а_п=10+9 , п=5

9. а₁=2, а_п=20, п=4; 10. а₁=5+ ,а_п=5-11 ,п=10.

Найти сумму п первых членов арифметической прогрессии:

1. 9;13;17;…, если п=11; 2. 25;30;35;…,если п=22;

3.-16;-10;-4;…,если п=12; 4.-3;4;11;…,если п=13;

5. 36;33;30;…,если п=20; 6. 27;25;23;…,если п=16;

7. ; ; ;…,если п=15; 8. ; ; ;…,если п=10;

9. 36;34;32,…,если п=5; 10.-38;-33;-28;…,если п=7.

Арифметическая последовательность задана формулой п-го члена.

Найдите S₅₀, если:

1. а_п= 3п+5; 2. а_п= 7+2п; 3. а_п= 4+3п; 4. а_п= 12-5п;

5. а_п= 3(п+1); 6. а_п= 4п-6; 7. а_п= 2п²-1; 8. а_п= 3п+5;

9. а_п= 1+ ; 10. а_п= (-2)^п.

Найдите а_п и d арифметической прогрессии, у которой:

1. а₁=10, п=14, S₁₄=1050; 2. а₁=40, п=20, S₂₀=-40;

3. а₁= , п=10, S₁₆=90 ; 4. а₁= , п=16, S₁₆=-10 ;

5. а₁=3, п=8, S₈=140; 6. а₁=5, п=9, S₉=17;7. а₁=2, п=6, S₆=72;

8. а₁=6, п=11, S₁₁=286;9. а₁=9, п=15, S₁₅=450;

10. а₁=3, п=16, S₁₆=648.

Найдите пятый член геометрической прогрессии

1. в₁=81 ,g= ; 2. в₁=4 ,g= 3; 3. в₁=16 ,g= ;

4. в₁=5 ,g= ; 5. в₁=4 ,g= -0,25; 6. в₁=16 ,g= 0.5;

7. в₁=1 ,g= ; 8. в₁=-2 ,g= -2; 9. в₁=-10 ,g= -20;

10. в₁=3 ,g= .

Найдите формулу п - го члена геометрической прогрессии:

1. 8,16,32,…; 2. 4,2,1,…; 3. 3,1, ,…; 4.3,2, ,…;

5.5,-5 ,10,…; 6.1,1,1,…; 7. –10,20,-4-,…; 8.-50,10,-2,…;

9. ; - ; ,…; 10. ; 3; 3 ;….

Найдите номер подчеркнутого члена геометрической прогрессии

1. 6, 12,24,…192,…; 2. 4,12,36,…324,…; 3. –1,2-4,…128,…;

4. 3а²,3а³,3а⁴,…3а¹³,…; 5. 2,2 ,4,…16 ,

6. 8,16,32,…512,…; 7. 625,125,25,,…192,…;

8. 6, 12,24,… ,…;9. 486,162,54,… ,…;10. 5,10,20,…320,….

Найдите первый член, знаменатель и формулу п-го члена геометрической прогрессии, если

1. в₂=12,в₅=324; 2. в₂=28,в₄=448; 3. в₂=12,в₅=324;

4. в₂=128,в₇=4; 5. в₃=3р⁶,в₁₀=3р²⁰; 6. в₄=24,в₇=192;

7. в₂=12,в₄=192; 8. в₃=-27,в₆=-1; 9. в₃=4р²,в₁₀=512р⁹;

10. в₂=4,в₄=1;

Содержимое разработки

Кондратова Лилия Николаевна.

Учитель математики

МОУ СОШ№4 г. Всеволожск

Тест.9класс.

Квадратичная функция и квадратичные неравенства.

Вариант№1

Найдите координаты вершины параболы

у= -2х²+8х-13.

(2;-5);

(-2;-9)

(2;-7);

(2;-5).

Найдите промежуток (промежутки)

возрастания функции

у=-2х²+7х-3.

(-;1,75;

1,75;+);

-3,5;+)

(-;3,5.

Найдите нули функции

у=-9х+7х².

0;-1 ;

0; ;

0;1 ;

0;- .

Найдите множество значений

функции у=х²+3х-5.

(-;-5;

-5;+);

(-;-7,25;

-7,25;+).

При каких значениях х значения функции

у= -х²-2х+8 положительны?

(-;-4) (2;+ );

(-4;2);

(-2;4);

(-;-2) (2;+ )

Решите неравенство

3х²-5х+20

(-;-1-2/3;+);

-1;- 2/3;

 2/3;1;

(-;2/31;+)

Решите неравенство

и укажите наименьшее целое решение этого неравенства.

-3;

-2;

-1;

Вариант № 2

	А	B	C	D
Найдите координаты вершины параболы у=2х²+12х+15.	(-6;15);	(-3;-6)	(3;69);	(-3;-3).
Найдите промежуток (промежутки) возрастания функции у=3х²-9х-4.	(-;1,5;	-1,5;+);	1,5;+)	(-;1,5.
Найдите нули функции у=6х-5х².	0;- ;	0;- ;	0;1,2;	0; .
Найдите множество значений функции у=-х²+5х-2.	(-;4,25;	4,25;+);	(-;-2;	-2;+).
При каких значениях х значения функции у= -х²-3х+4 отрицательны?	(-;-4) (1;+ );	(-1;4);	(-4;1);	(-;-1) (4;+ )
Решите неравенство -4х²+5х-10	(-;0,251;+);	-0,25;1;	-1;-0,25;	(-;-1-0,25;+)
Решите неравенство и укажите наименьшее целое решение этого неравенства.	0;	-1;	-2;	1. 1.

Содержимое разработки

Кондратова Лилия Николаевна.

Учитель математики

МОУ СОШ№4 г. Всеволожск

Вариант№1

Зачет.8класс (4;5)

Неравенства

1.Сформулируйте определения понятий «меньше» и «больше». Сравните числа а и в, если:

а-в=-0,24; а-в=0; а-в=(-0,45)⁶

2.Докажите неравенство:

(а-4)(а+7)(а+5)(а-2); .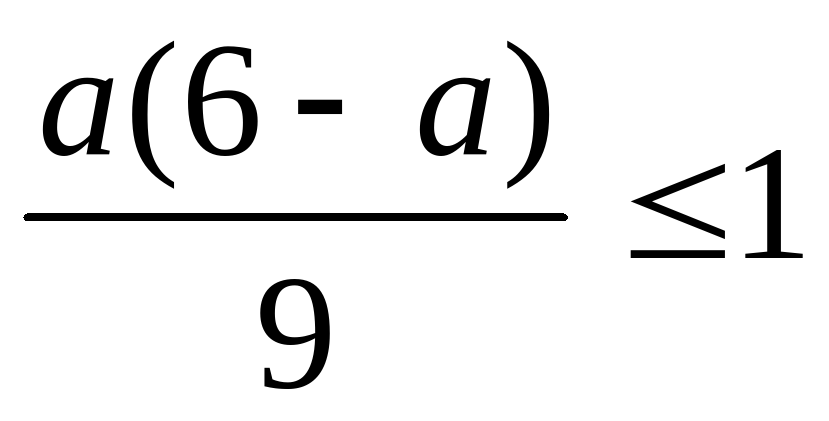

3.Сформулируйте теоремы. Выражающие свойства числовых неравенств.

а)Сравните числа а и в, если а  с, в  с.

в)Зная ,что а в, сравните а-5 и в-5;

13а и 13в; -9а и –9в; 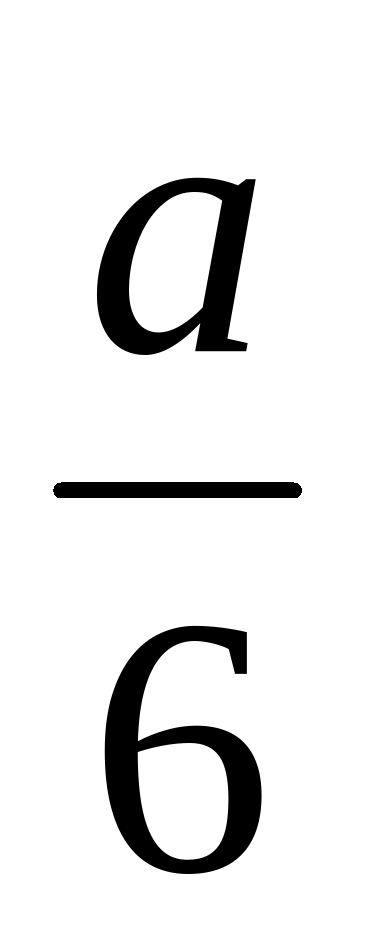и

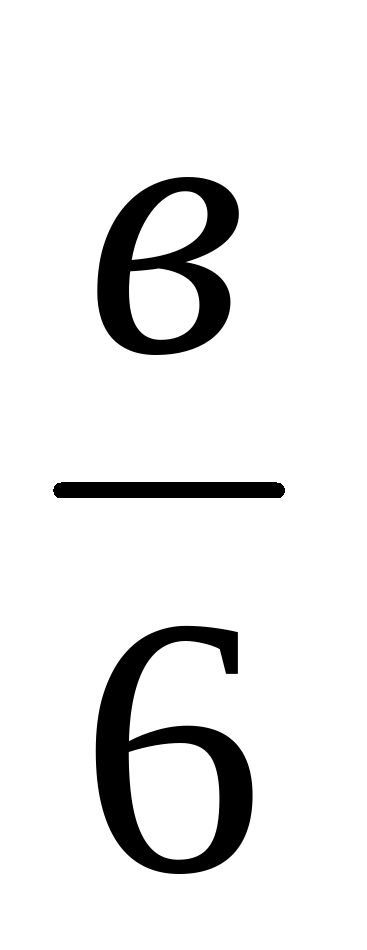
4.Сформулируйте теорему о сложении неравенств.

а)Выполните сложение неравенств 12-3 и -6-18.

в)Докажите ,что если а4 и в3, то 5а+3в29.

5. Сформулируйте теорему об умножении неравенств.

а)Выполните умножение неравенств 614 и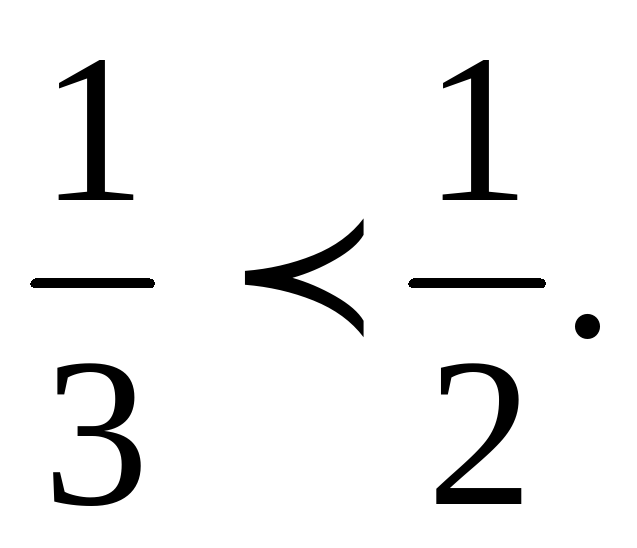

6.Какие неравенства называют строгими; нестрогими?

а)Укажите наибольшее целое число, удовлетворяющее неравенству а6; а0

в)Укажите наименьшее целое число, удовлетворяющее неравенству а8; а-3.

7.Является ли число 4 решением неравенства 5х-211?

Что называется решением неравенства с одним неизвестным? Что значит решить неравенство?

8.Сформулируйте свойства, которые используются при решении неравенств.

Решите неравенство и укажите , какие свойства использовались при его решении:

х-64; 8х32; -3х-9; х/51.

9.Решите неравенство:

4(2х-1)-3(х+2) 5; .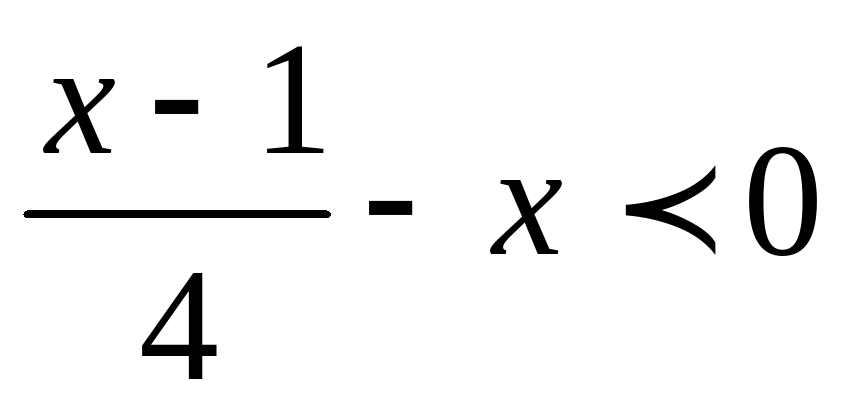

10.Является ли число 5 решением системы неравенств

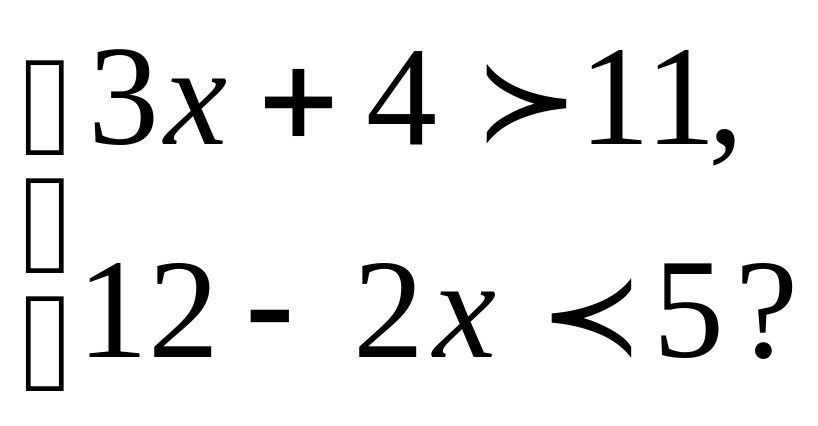
Что называется решением системы неравенств? Что значит решить систему неравенств?

11. Решите систему неравенство:

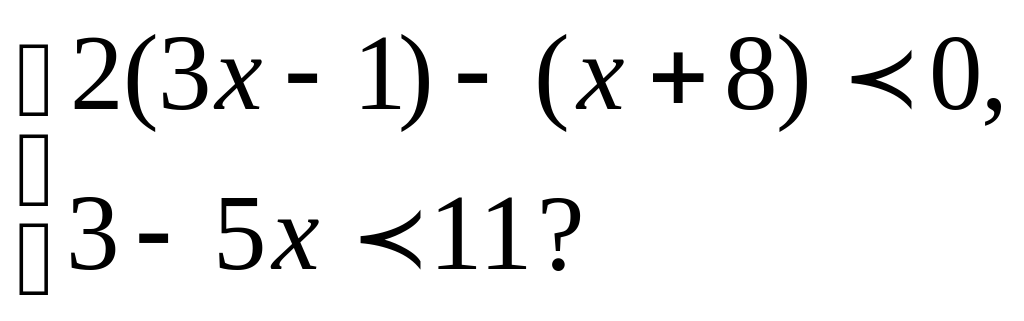
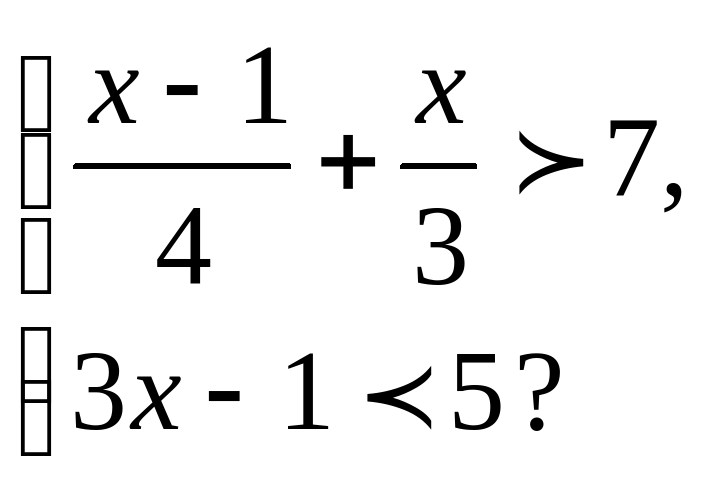
12. Решите неравенство, содержащее переменную под знаком модуля:

5х-14; 3-2х7.

13.Решить двойное неравенство

6 -6х 12.

Вариант№1

Зачет.8класс (3;4)

Неравенства

1.Сформулируйте определения понятий «меньше» и «больше». Сравните числа а и в, если:

а-в=0,016; а-в=0; а-в=(-0,3)⁷

2.Докажите неравенство:

(а-5)(а+7) (а+12)(а-10); .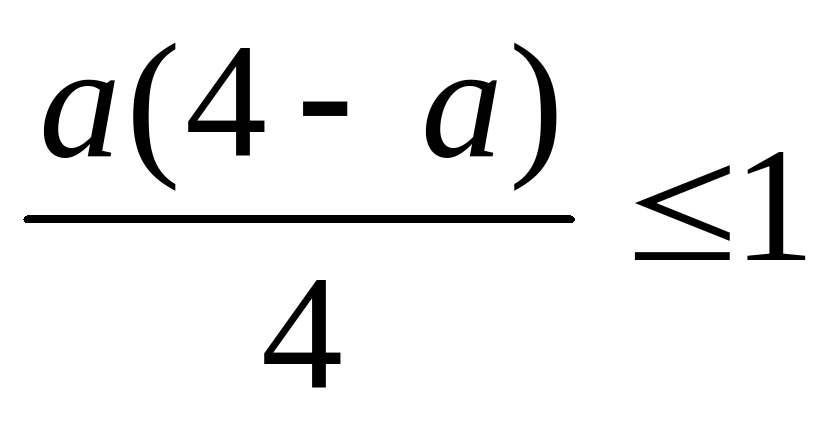

3.Сформулируйте теоремы, выражающие свойства числовых неравенств.

а)Сравните числа а и с, если а в и св

в)Зная ,что а в, сравните а+4 и в+4;

8а и 8в; -14а и –14в;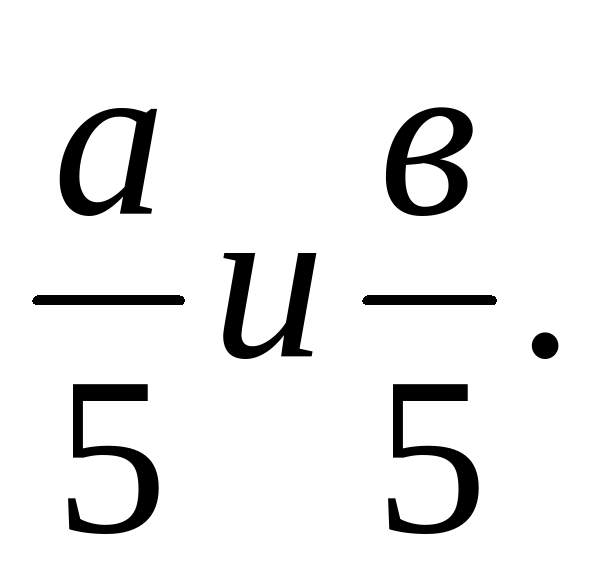

4.Сформулируйте теорему о сложении неравенств.

Зная, что 8а9 и 4в5, оцените сумму а+в и разность а-в.

5. Сформулируйте теорему об умножении неравенств.

Зная , что 11х12 и 2у3, оцените произведение ху и частное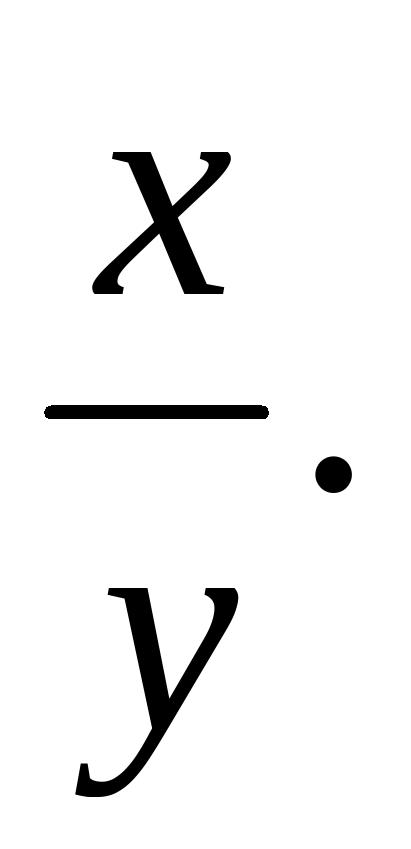

6. Изобразите на координатной прямой множество чисел х, если:

ахв; ахв; ха; хв.

7.Является ли число 3 решением неравенства 2х-13?

Что называется решением неравенства? Что значит решить неравенство?

8.Сформклируйте свойства равносильности, которые используются при решении неравенств.

Решите неравенство и укажите , какое свойство равносильности использовалось при его решении:

х+1116; 12х3,6; -15х-45; х/4-2.

9.Решите неравенство:

5(х-0,2)-0,4(3-х)  51 .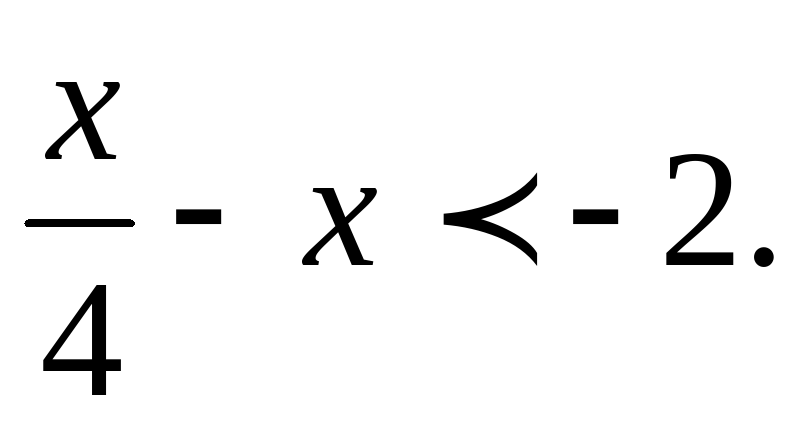

10.Является ли число -3 решением системы неравенств

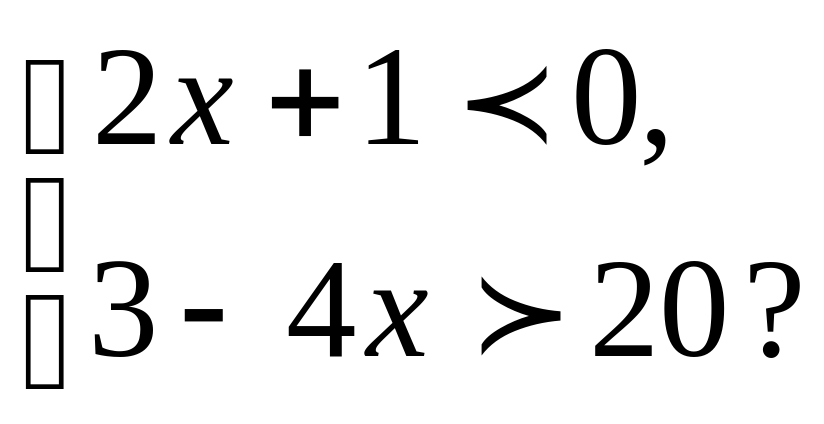
Что называется решением системы неравенств? Что значит решить систему неравенств?

11. Решите систему неравенств:

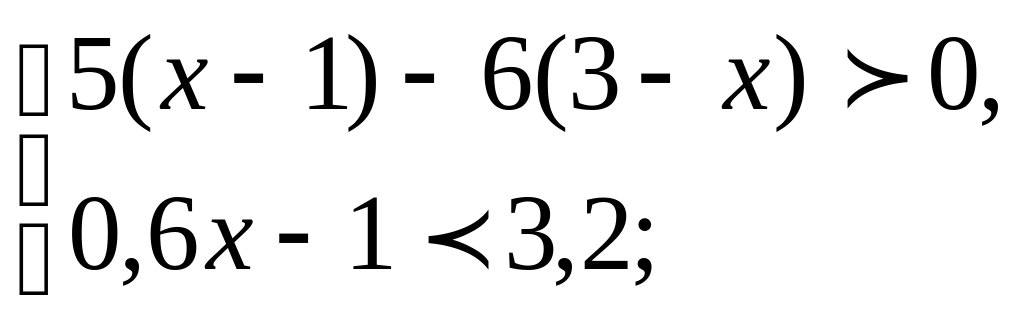
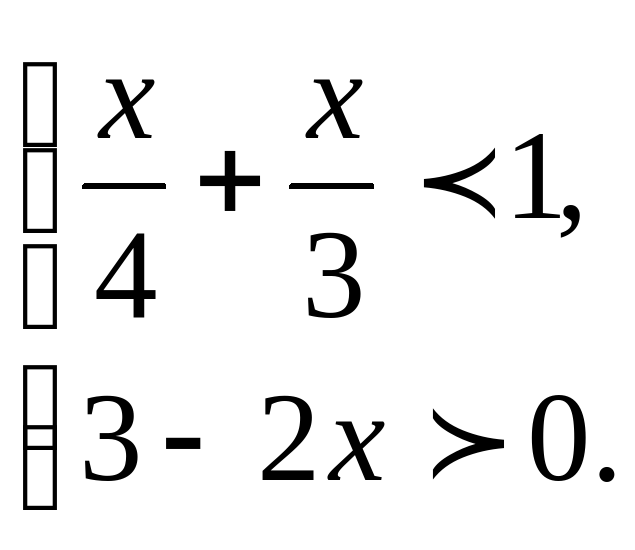
12. Решите двойное неравенство:

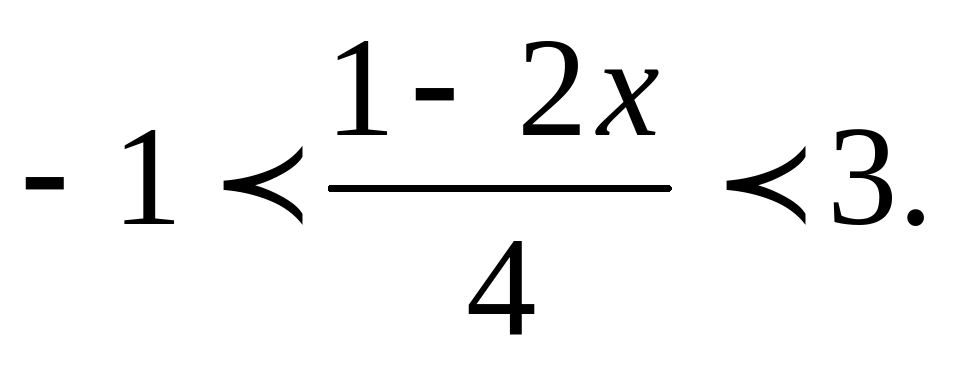Вариант№2

Зачет.8класс (4;5)

Неравенства

1.Сформулируйте определения понятий «меньше» и «больше». Сравните числа а и в, если:

а-в=-0,16; а-в=0; а-в=(-0,32)⁷

2.Докажите неравенство:

(а-3)(а-5) (а-3)²; .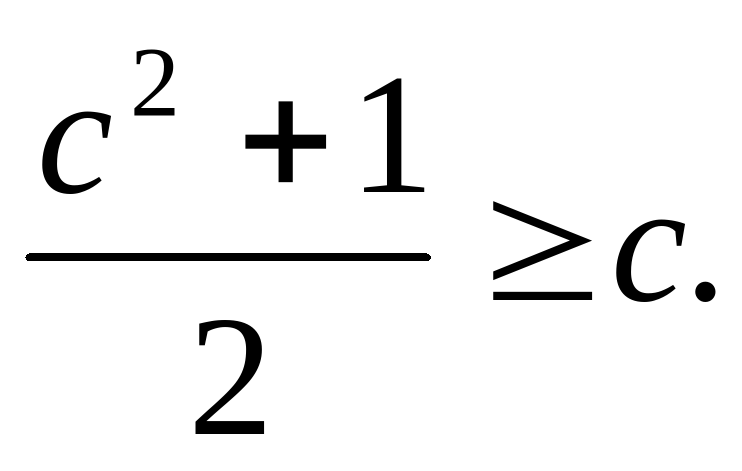

3.Сформулируйте теоремы. Выражающие свойства числовых неравенств.

а)Сравните числа а и в, если а  с, в  с.

в)Зная ,что а в, сравните а-6 и в-6;

17а и 17в; -8а и –8в; 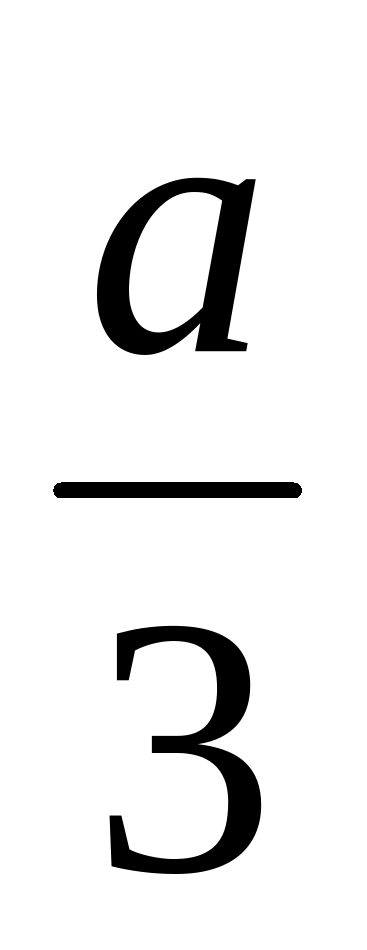и

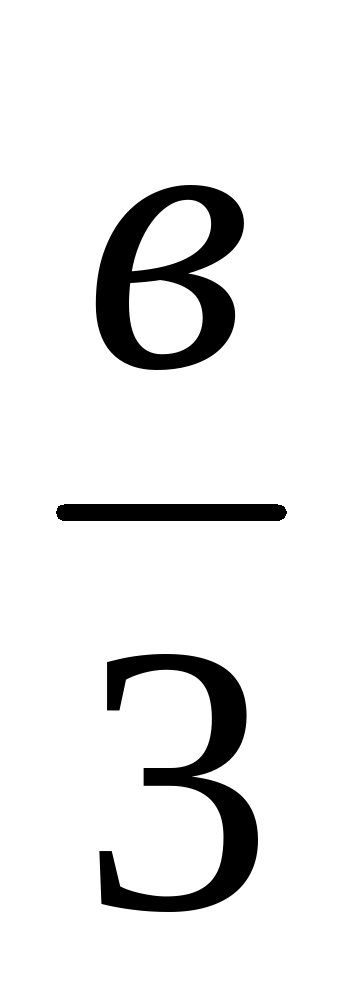
4.Сформулируйте теорему о сложении неравенств.

а)Выполните сложение неравенств 11-3 и -5-7.

в)Докажите ,что если а3 и в2, то 8а+2в24.

5. Сформулируйте теорему об умножении неравенств.

а)Выполните умножение неравенств 915 и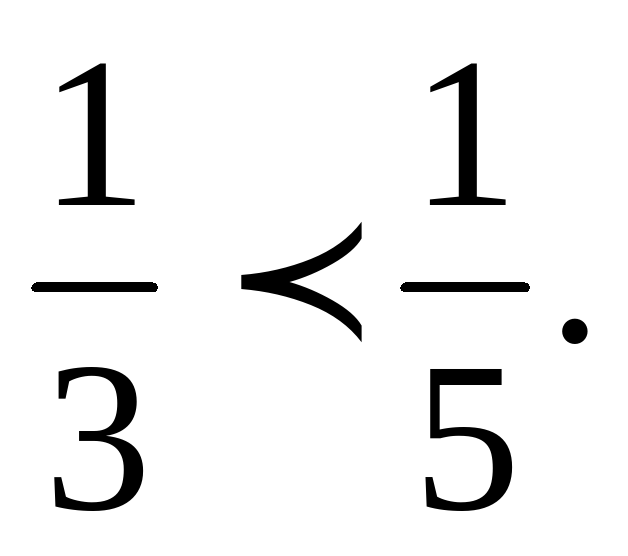

6.Какие неравенства называют строгими; нестрогими?

а)Укажите наибольшее целое число, удовлетворяющее неравенству а9; а0

в)Укажите наименьшее целое число, удовлетворяющее неравенству а7; а-2.

7.Является ли число 3 решением неравенства 7х-510?

Что называется решением неравенства с одним неизвестным? Что значит решить неравенство?

8.Сформулируйте свойства, которые используются при решении

Решите неравенство и укажите , какие свойства использовались при его решении:

х-53; 9х27; -5х-45; х/31.

9.Решите неравенство:

6(2х-1)-(х+2)  0; .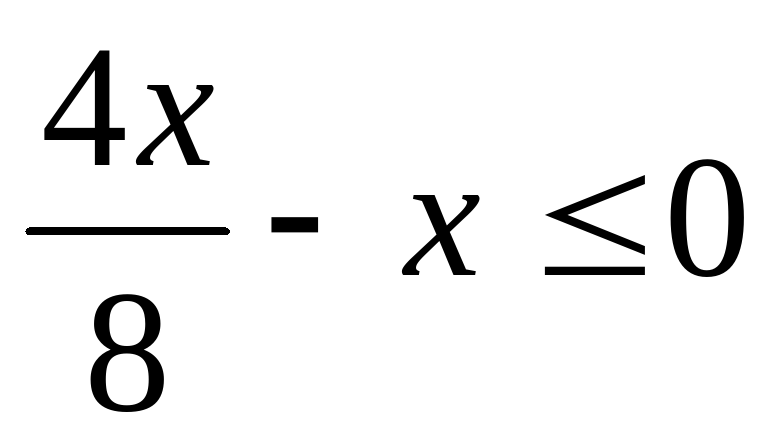

10.Является ли число 2 решением системы неравенств

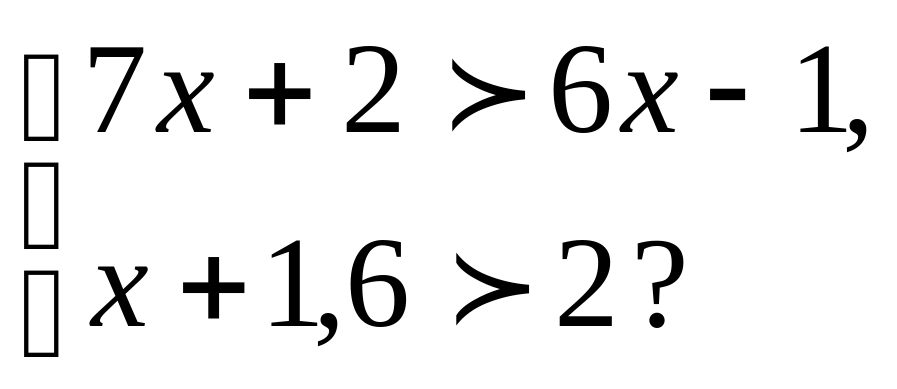
Что называется решением системы неравенств? Что значит решить систему неравенств?

11. Решите систему неравенство:

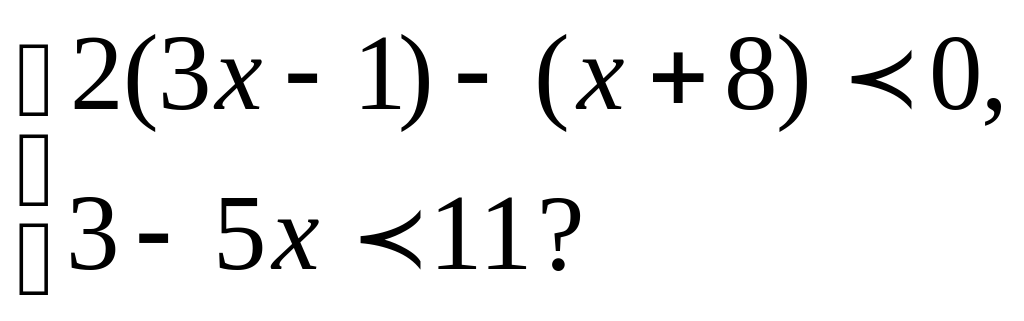
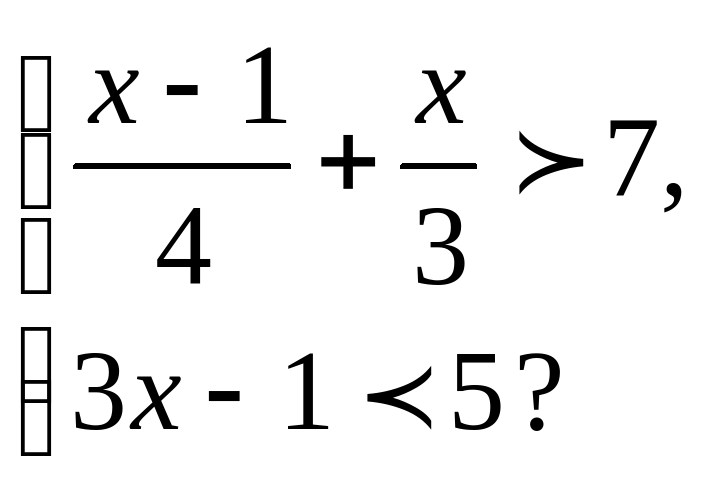
12. Решите неравенство, содержащее переменную под знаком модуля:

5-х1; 6+5х7 1.

13.Решить двойное неравенство:

3,55х10.

Вариант№2

Зачет.8класс (3;4)

Неравенства

1.Сформулируйте определения понятий «меньше» и «больше». Сравните числа а и в, если:

а-в=0,15; а-в=0; а-в=(-0,2)⁶

2.Докажите неравенство:

(а-5)(а+7) (а+12)(а-10); .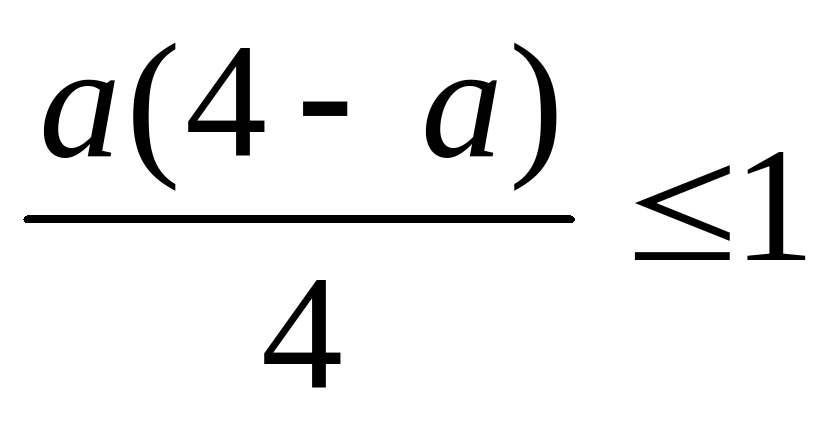

3.Сформулируйте теоремы, выражающие свойства числовых неравенств.

а)Сравните числа а и с, если а в и св

в)Зная ,что а в, сравните а+4 и в+4;

8а и 8в; -14а и –14в;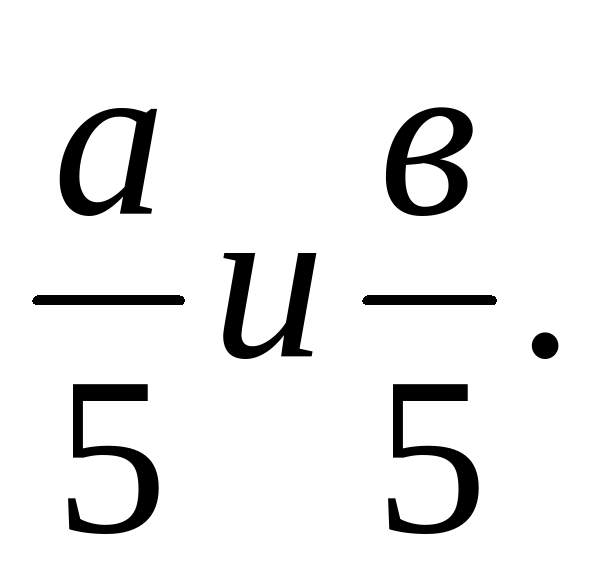

4.Сформулируйте теорему о сложении неравенств.

Зная, что 8а9 и 4в5, оцените сумму а+в и разность а-в.

5. Сформулируйте теорему об умножении неравенств.

Зная , что 11х12 и 2у3, оцените произведение ху и частное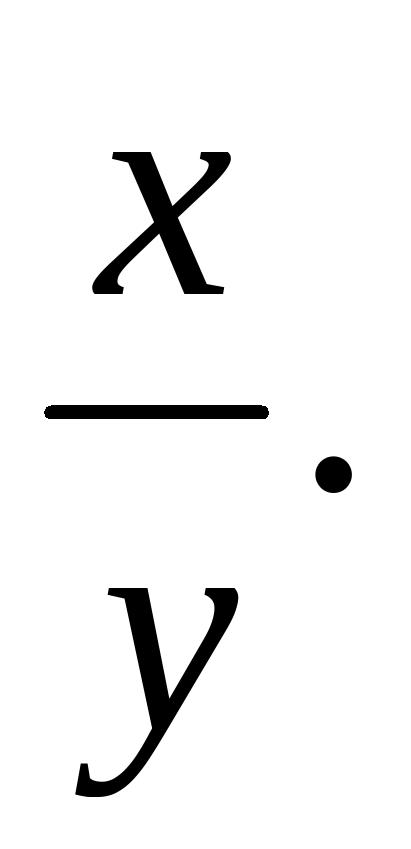

6. Изобразите на координатной прямой множество чисел х, если:

ахв; ахв; ха; хв.

7.Является ли число 3 решением неравенства 2х-13?

Что называется решением неравенства? Что значит решить неравенство?

8.Сформклируйте свойства равносильности, которые используются при решении неравенств.

Решите неравенство и укажите , какое свойство равносильности использовалось при его решении:

Х+1116; 12х3,6; -15х-45; х/4-2.

9.Решите неравенство:

5(х-0,2)-0,4(3-х)  51 .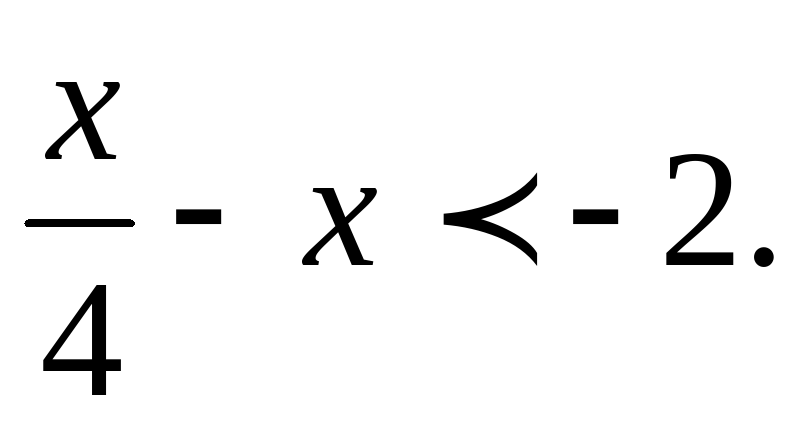

10.Является ли число -3 решением системы неравенств

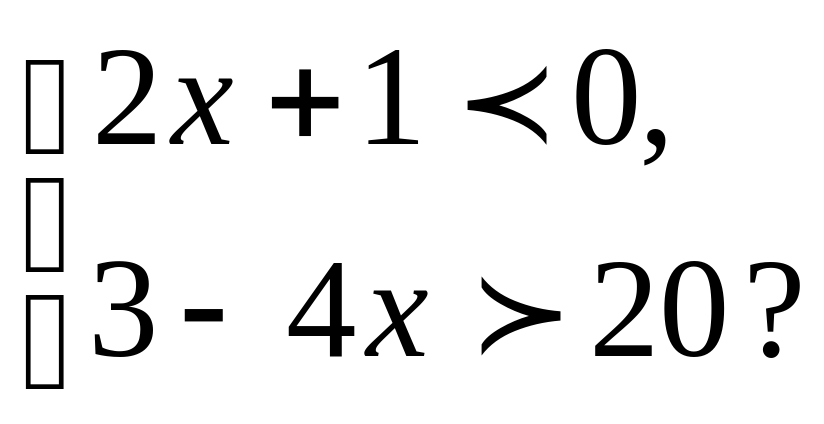
Что называется решением системы неравенств? Что значит решить систему неравенств?

11. Решите систему неравенств:

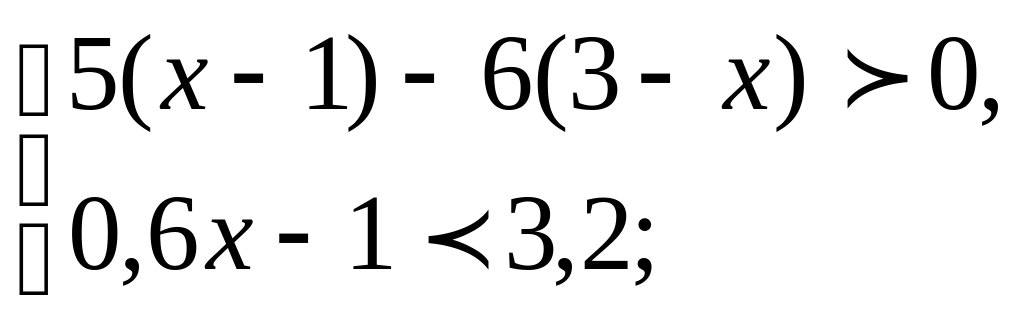
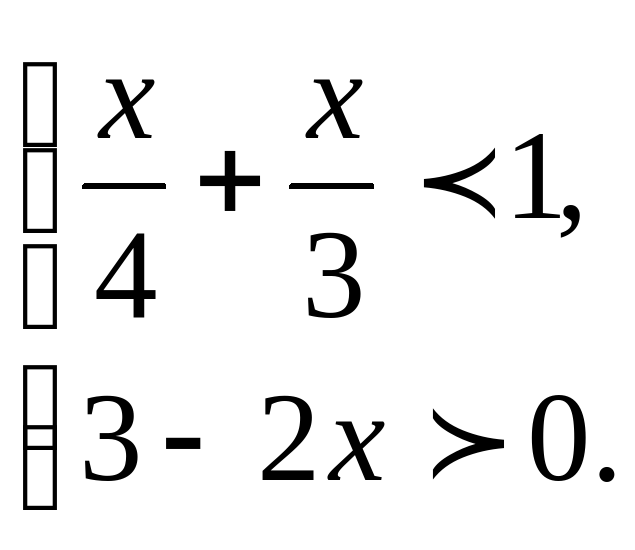
12. Решите двойное неравенство:

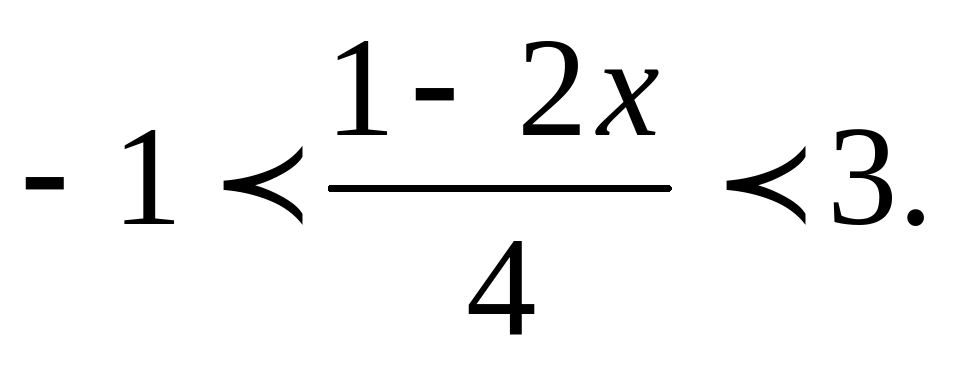Вариант№3

Зачет.8класс (4;5)

Неравенства

1.Сформулируйте определения понятий «меньше» и «больше». Сравните числа а и в, если:

а-в=-0,25; а-в=0; а-в=(-0,4)⁷

2.Докажите неравенство:

(а+2)²а(а-4); .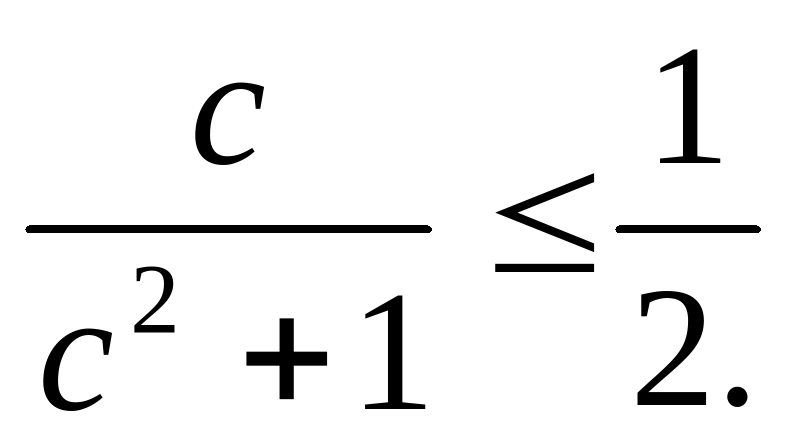

3.Сформулируйте теоремы. Выражающие свойства числовых неравенств.

а)Сравните числа а и в, если а  с, в  с.

в)Зная ,что а в, сравните а-8и в-8;

19а и 19в; -7а и –7в; 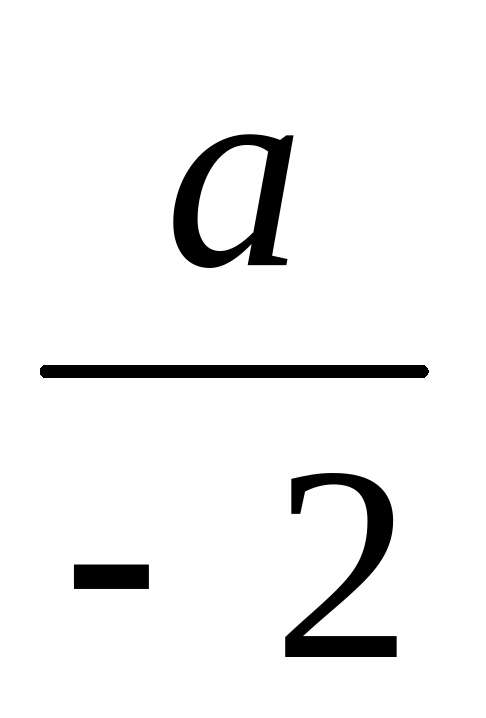и

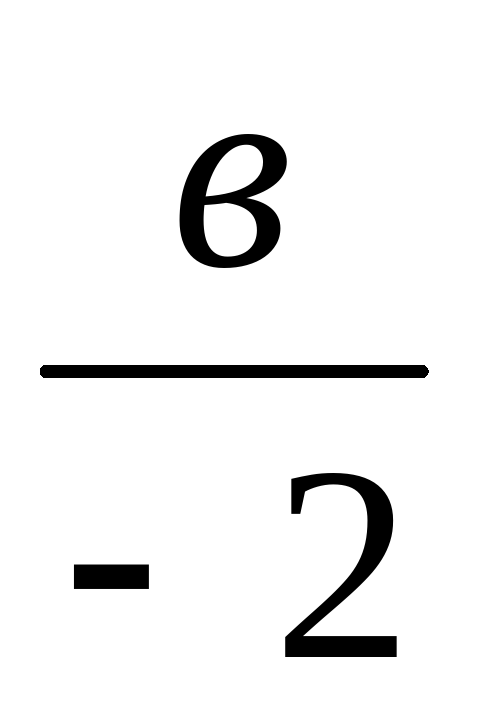
4.Сформулируйте теорему о сложении неравенств.

а)Выполните сложение неравенств 10-2 и -2-15.

в)Докажите ,что если а2 и в4, то 3а+4в22.

5. Сформулируйте теорему об умножении неравенств.

а)Выполните умножение неравенств 812 и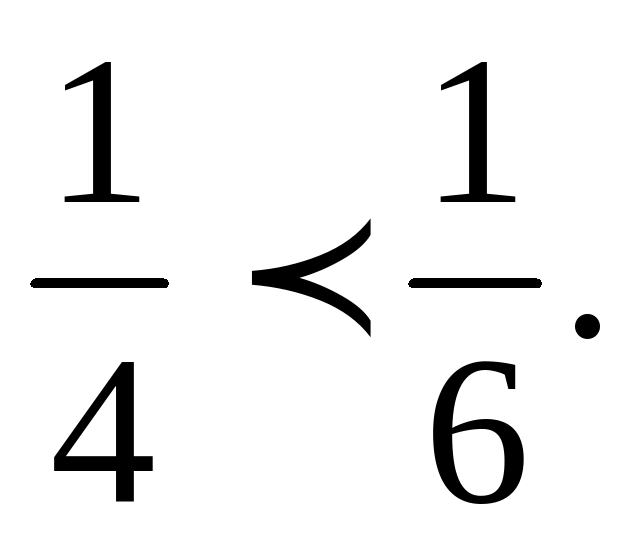

6.Какие неравенства называют строгими; нестрогими?

а)Укажите наибольшее целое число, удовлетворяющее неравенству а8; а0

в)Укажите наименьшее целое число, удовлетворяющее неравенству а4; а-5.

7.Является ли число 9 решением неравенства 3х-12?

Что называется решением неравенства с одним неизвестным? Что значит решить неравенство?

8.Сформулируйте свойства, которые используются при решении

Решите неравенство и укажите , какие свойства использовались при его решении:

х-42; 6х48; -7х-56; х/71.

9.Решите неравенство:

4(1-х)+5(х+8) 0 ; .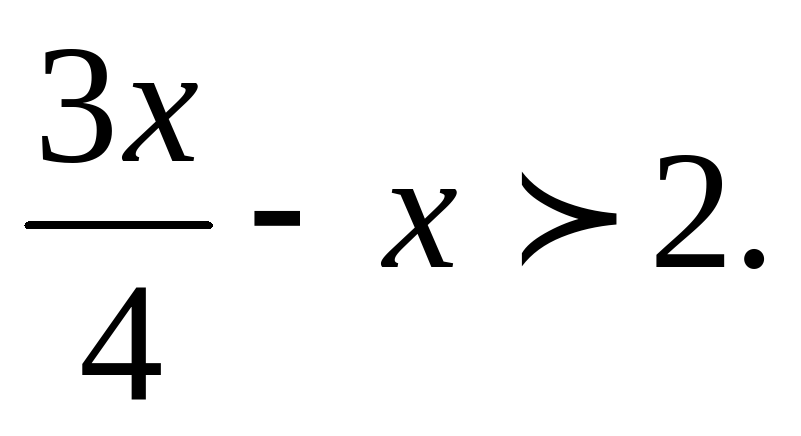

10.Является ли число 3 решением системы неравенств

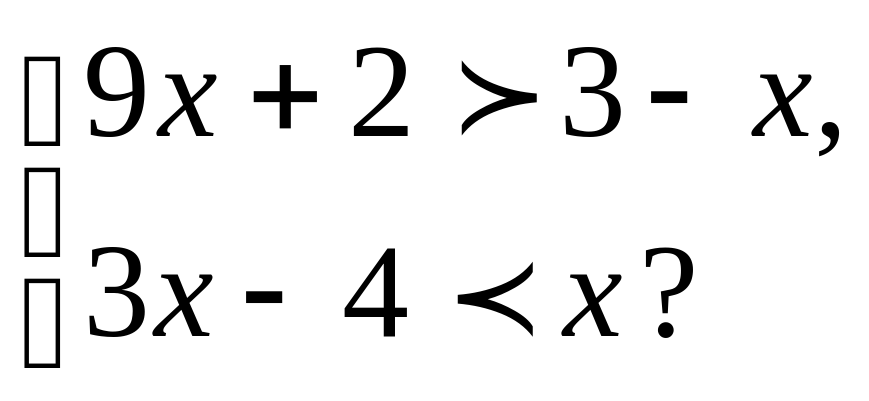
Что называется решением системы неравенств? Что значит решить систему неравенств?

11. Решите систему неравенство:

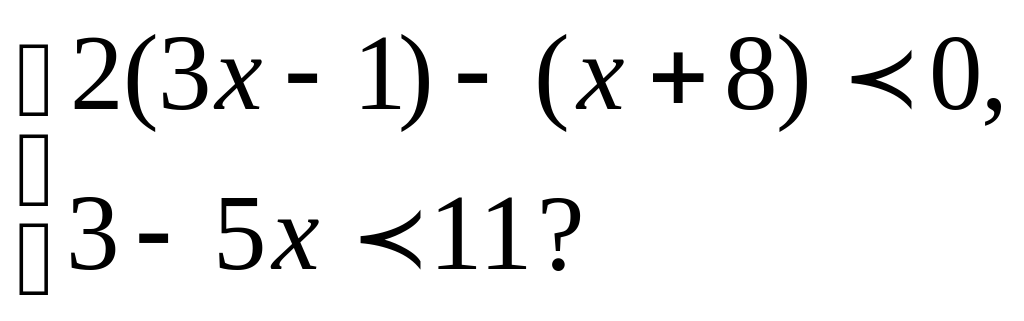
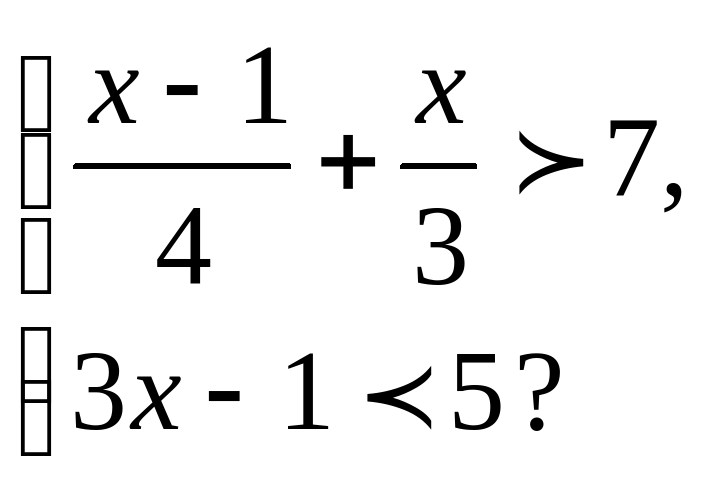
12. Решите неравенство, содержащее переменную под знаком модуля:

6+5х41 4х+13.

13.Решить двойное неравенство:

0,5 4,5.

Вариант№3

Зачет.8класс (3;4)

Неравенства

1.Сформулируйте определения понятий «меньше» и «больше». Сравните числа а и в, если:

а-в=0,15; а-в=0; а-в=(-0,2)⁶

2.Докажите неравенство:

(а-5)(а+7) (а+12)(а-10); .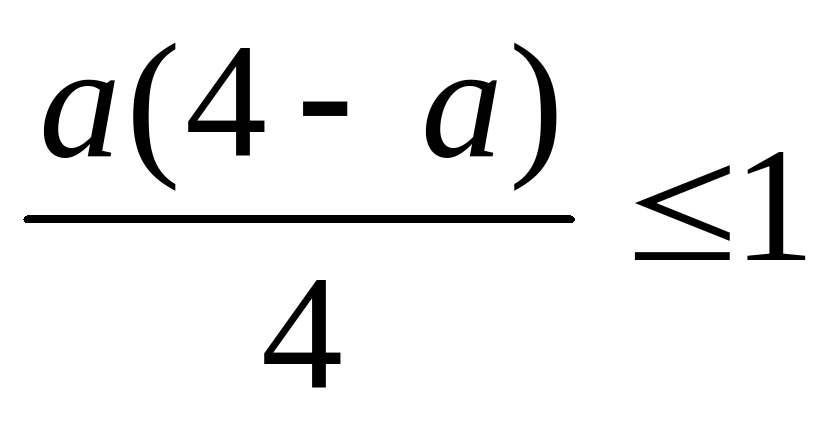

3.Сформулируйте теоремы, выражающие свойства числовых неравенств.

а)Сравните числа а и с, если а в и св

в)Зная ,что а в, сравните а+4 и в+4;

8а и 8в; -14а и –14в;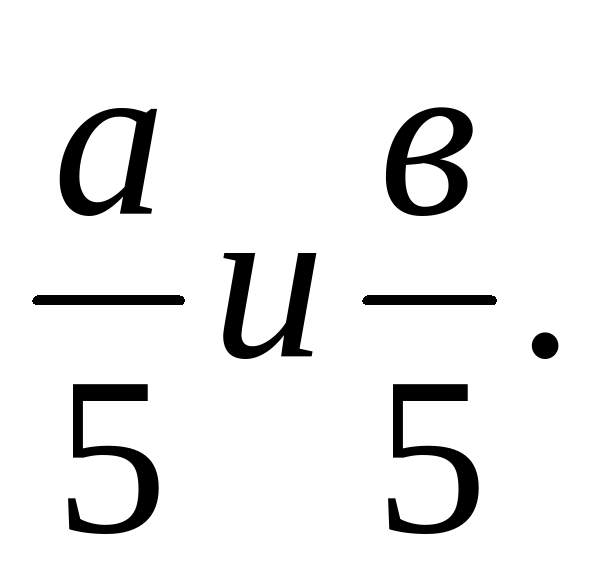

4.Сформулируйте теорему о сложении неравенств.

Зная, что 8а9 и 4в5, оцените сумму а+в и разность а-в.

5. Сформулируйте теорему об умножении неравенств.

Зная , что 11х12 и 2у3, оцените произведение ху и частное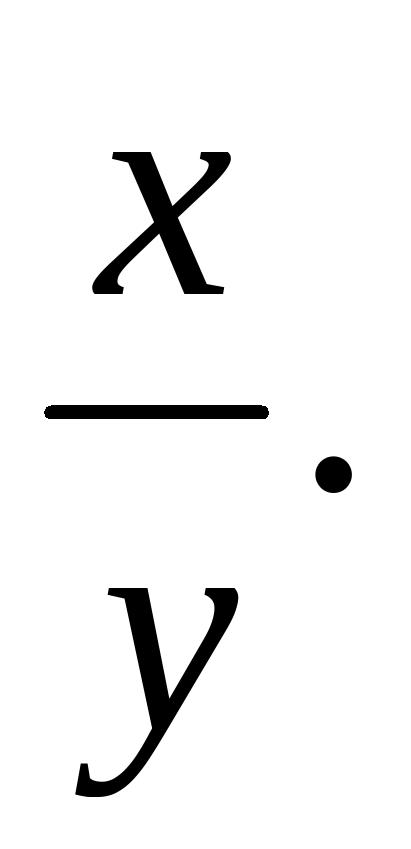

6. Изобразите на координатной прямой множество чисел х, если:

ахв; ахв; ха; хв.

7.Является ли число 3 решением неравенства 2х-13?

Что называется решением неравенства? Что значит решить неравенство?

8.Сформулируйте свойства равносильности, которые используются при решении неравенств. Решите неравенство и укажите , какое свойство равносильности использовалось при его решении:

Х+1116; 12х3,6; -15х-45; х/4-2.

9.Решите неравенство:

5(х-0,2)-0,4(3-х)  51 .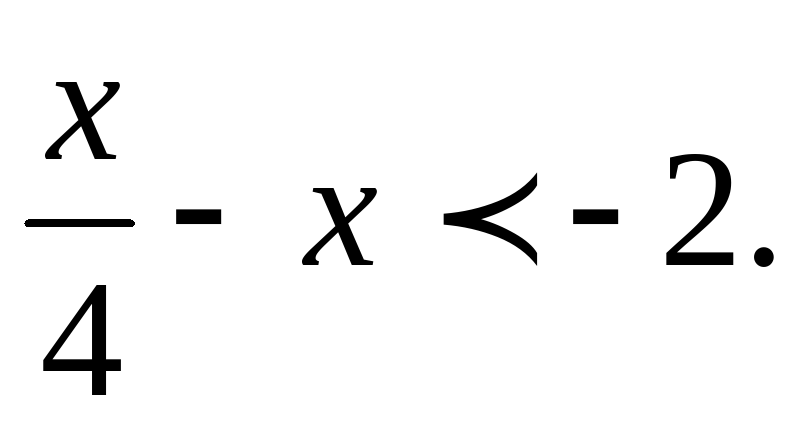

10.Является ли число -3 решением системы неравенств

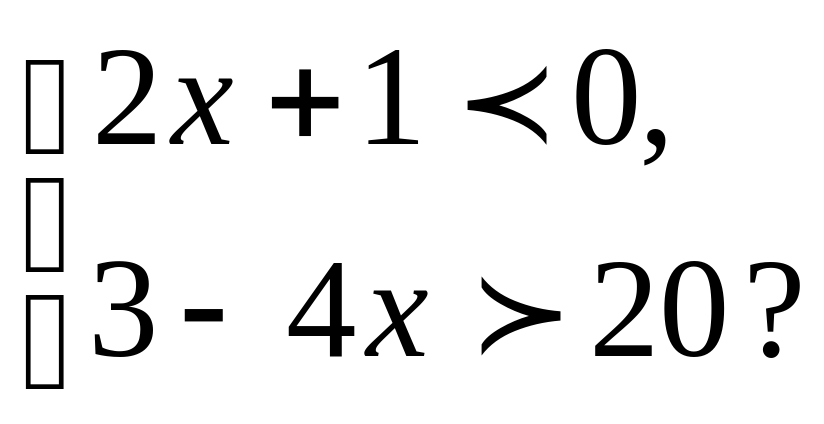
Что называется решением системы неравенств? Что значит решить систему неравенств?

11. Решите систему неравенств:

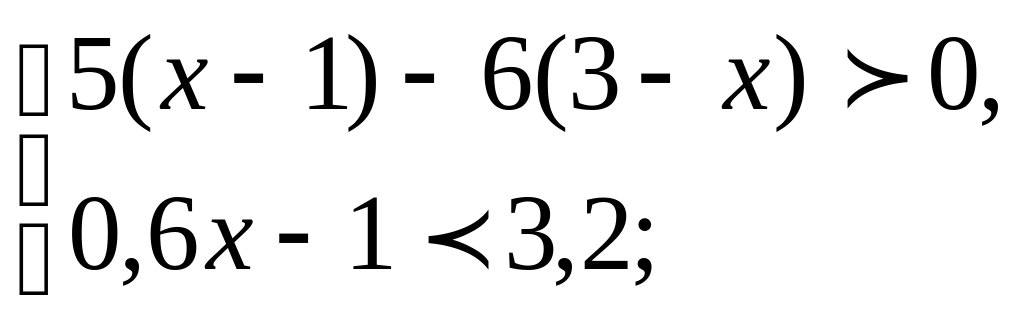
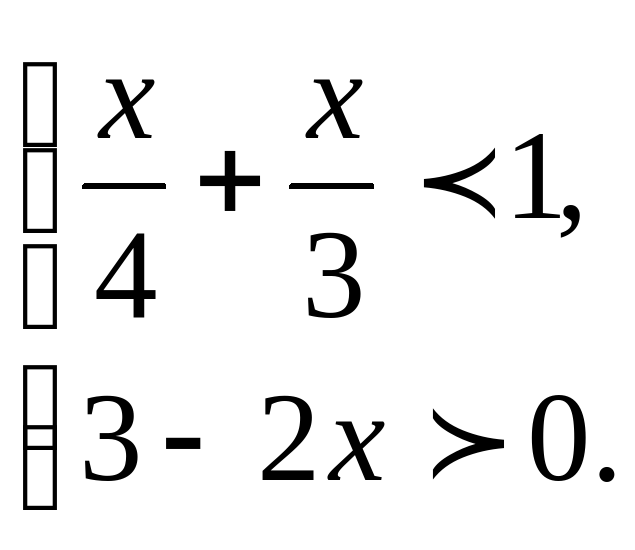
12. Решите двойное неравенство:

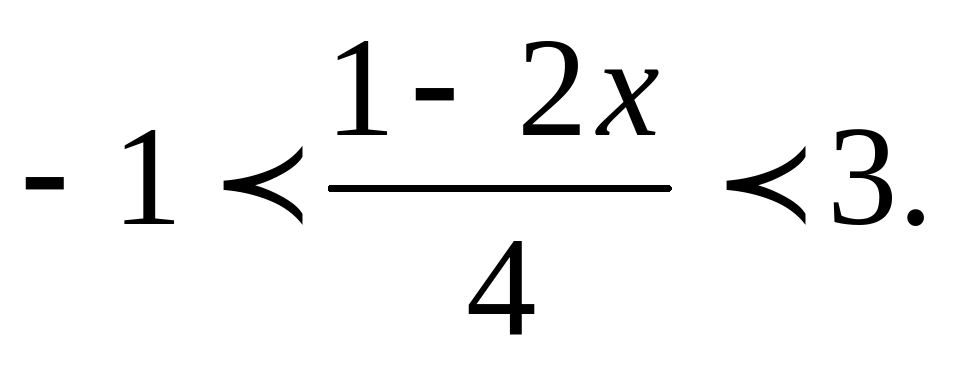Содержимое разработки

Кондратова Лилия Николаевна.

Учитель математики

МОУ СОШ№4 г. Всеволожск

9 класс

Тест

Арифметическая и геометрическая прогрессии

Вариант№1

А В С D

1.В арифметической прогрессии

а₅=8,7 иа₈=12,3. Найдите d и a₁ 1,6 3,6 1,2 1,4

2,3; -5,7; 3,9; 3,1.

2.В арифметической прогрессии

а₁=-7,3 и а₂=-6,4.В каком месте

(укажите номер) находиться

число 26? 39; 38; 27; 28.

3.В арифметической прогрессии

а₁=38,1 и а₂=36,7.В каком месте

(укажите номер) стоит отрицат

ельное число? Найдите это число. -0,5; -0,7; -1,1; -0,3.

4.Найдите сумму первых шестна

дцати членов арифметической

прогрессии, заданной формулой

а_п=6_п+2. 864; 848; 792; 716.

5.В геометрической прогрессии

а₁=722; а₃82. Найдите знамена

тель g. 9; 3; ; и-

6.В геометрической прогрессии

а₁= и а₂= .Найдите шестой член

прогрессии. ; 5 ; ; 10 .

7. В геометрической прогрессиив₁=0,4

и в₂=1,2.Найдите сумму пяти членов

этой прогрессии. 18,8; 80,2; 48,4; 39,6.

8.Найдите первый член геометрической

прогрессии, если а₁+а₅=20 и а₂+а₃=17. 4; 6; 2; 8.

9.Для периодической дроби 0,41(6)

найдите несократимую обыкновенную

дробь. Запишите разность числителя и

знаменателя. 12; 7; 8; 11.

10.Д а н о:(в_п)-геометрическая

прогрессия, в₁=3, g=2. Какой цифрой

оканчивается в₂₀? 6; 2; 8; 4.

9 класс

Тест

Арифметическая и геометрическая прогрессии

Вариант№2

А В С D

1.В арифметической прогрессии

а₃=7,5 иа₇=14,3. Найдите d и a_1. 6,8 3,4 1,7 1,4 -6,1; 0,7; 4,1; 4,7.

2.В арифметической прогрессии

а₁= -5,6 и а₂= - 4,8.В каком месте

(укажите номер) находиться

число 16? 14; 13; 27; 28.

3.В арифметической прогрессии

а₁=29,2 и а₂=27,9.В каком месте

(укажите номер) стоит первое

отрицательное число? Найдите

это число. -1,1; -0,9; -0,7; -0,3.

4.Найдите сумму первых восемна

дцати членов арифметической

прогрессии, заданной формулой

а_п=4_п+9. 732; 846; 768; 934..

5.В геометрической прогрессии

а₁=363; а₃₌93. Найдите знамена

тель g. 2; ; ; и-

6.В геометрической прогрессии

а₁=- и а₂= .Найдите пятый член

этой прогрессии. 13 4 40,5; -13,5; - .

7. В геометрической прогрессиив₁=-0,3

и в₂=-0,6.Найдите сумму шести членов

этой прогрессии. -9,3; 6,3; 3,2; -18,9.

8.Найдите первый член арифметрической

прогрессии, если а₁+а₆=26 и а₂+а₃=18. 3; 2; 4; 1,5.

9.Для периодической дроби 0,58(3)

найдите несократимую обыкновенную

дробь. Запишите разность числителя

и знаменателя. 3; 7; 5; 2.

10.Д а н о:(в_п)-геометрическая прогрессия,

в₁=2, g=3. Какой цифрой оканчивается в₁₅? 6; 8; 4; 2.

Содержимое разработки

СЛАЙД 1 Открытый урок по алгебре на тему :

”Графический способ решения систем уравнений.”

Содержание урока.

1. Организационный момент, характеризующийся внешней и

внутренней (психологической) готовностью учащихся к уроку.

2. Постановка образовательных, воспитательных и развивающих задач.

3.Проверка домашнего задания методом решений аналогичных примеров.

4. Актуализация или этап закрепления знаний. Подготовка к ГИА.

5. Этап информации о домашнем задании, инструктаж по выполнению.

6.Рефлексия

СЛАЙД 3

Цели урока:

Образовательная: Научиться анализировать данные для нахождения решения системы уравнений по графику.
Научиться решать графически системы уравнений. Подготовиться к ГИА.

Развивающая: способствовать формированию умений применять приемы: обобщения, сравнения, выделения главного, переноса знаний в новую ситуацию, развитию математического кругозора, мышления и речи, внимания и памяти; установление закономерности многообразия связей для достижения уровня системности знаний.

Воспитательная: содействовать воспитанию интереса к математике, активности, организованности, умения общаться, выражать и отстаивать собственное мнение.

Тип урока: урок практикум
Методы обучения: частично-поисковый (эвристический), метод самопроверки, взаимопроверки.
Формы организации урока:

индивидуальная, фронтальная и коллективная.

Оборудование: доска, учебник, дидактические материалы,

карточки с заданиями,

мультимедиа.

СЛАЙД 5 Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их.

(Дьёрдь Пойа)

(Давайте же и мы с вами последуем совету венгерского математика Дьёрдя Пойа и начнём решать и строить. Вы сегодня поделены на 4 группы. У каждой группы есть свой ответственный, у которого есть таблица оценивания. В данные таблицы мои помощники будут вписывать баллы за вашу работу на уроке. Оценивание будет проводиться в 10–ти бальной системе.В конце урока ответственные групп подсчитают ваши баллы и мы их переведём в оценки.)

СЛАЙД 6 (Давайте начнём с повторения: повторим построение графика линейной функции, графика обратной пропорциональности, функции y=kx³, построение окружности и квадратичной функции.

Вместе вспомним алгоритм построения графика линейной функции(обсуждение слайда 6) и аналогично данному примеру вы построете графики других функций, которые мы с вами изучили. По решению данных примеров и проверим ваше домашнее задание. На ваших рабочих столах подготовлены индивидуальные карточки для каждой группы. Прошу ответственных выбрать по одному человеку для решения первого задания у доски. Остальные ученики решают пример на месте и затем оцениваются все моими помощниками. На решение данного задания даётся 5 минут)

РЕШАЮТ ЗАДАНИЯ

(Давайте теперь проверим правильность решения ваших уравнений.

обратная пропорциональность – СЛАЙД 7

функции y=kx³ - СЛАЙД 8

окружность – СЛАЙД 9

квадратичная функция – СЛАЙД 10- 13

Молодцы. Все хорошо выполнили задание на повторение.)

Мы с вами выучили графические способы решений уравнений. На сегодняшнем уроке мы переходим к графическому способу решения систем уравнений. Так как в системе у нас не одно, а несколько уравнений, то графики данных функций мы будем изображать на одной координатной плоскости. Рассмотрим пример, где в системе 3 уравнения разных видов. Обсуждаются СЛАЙДЫ 14-16.

Для закрепления знаний решим несколько систем уравнений. У каждой группы на столах есть задание. Прошу ответственных выбрать по одному человеку для решения задания у доски. Остальные ученики решают пример на месте На решение данного задания даётся 10-12 минут)

РЕШАЮТ ЗАДАНИЯ

(Давайте теперь проверим правильность решения ваших уравнений.

Задание 1 – СЛАЙД 17-18

Задание 2 - СЛАЙД 19-20

Задание 3– СЛАЙД 21

Задание 4– СЛАЙД 22)

(Мы плодотворно поработали. Я предлагаю немножко расслабиться – порешаем забавные загадки – СЛАЙД 23.Молодцы )

(Следующим этапом нашего урока будет подготовка к ГИА. У каждой группы на столах даны задания. Прошу одного человека с группы решить задание на доске и подробно объяснить его .Проверим правильность решений– СЛАЙДЫ 24-27.

Ответственные, подсчитайте, пожалуйста, баллы всех учеников из ваших групп . СЛАЙД 28)

СПАСИБО ЗА РАБОТУ. ДО СВИДАНИЯ.

Содержимое разработки

Цели урока:

Научить анализировать данные для нахождения решения системы уравнений по графику.

Научить решать графически системы уравнений.

Тема урока: «Решение систем уравнений второй степени».

Три пути ведут к знанию: путь размышления – это

путь самый благородный, путь подражания – это

путь самый лёгкий и путь опыта – это путь самый

горький.

Конфуций.

Цель урока: закрепить формирование навыков сознательного выбора решения системы; развивать потребность в нахождении рациональных способов решения; воспитывать умение контролировать внимание на всех этапах урока.

Психологическая установка учащимся:

1.Продолжаем отрабатывать навыки решения систем уравнений; продолжаем учиться решать задачи; формируем математическую интуицию, которая поможет ориентироваться в способах решения систем.

2.На уроке можно ошибаться, сомневаться, консультироваться.

3.Дать самому себе установку: «понять и быть тем первым, который увидит ход решения».

Сохранить у себя:

Карточки и тесты по алгебре в 9 классе

Карточки и тесты по алгебре в 9 классе

Содержимое разработки

Содержимое разработки

Кондратова Лилия Николаевна.

Учитель математики

МОУ СОШ№4 г. Всеволожск

Тест.9класс.

Квадратичная функция и квадратичные неравенства.

Вариант№1

Вариант № 2

Содержимое разработки

Кондратова Лилия Николаевна.

Учитель математики

МОУ СОШ№4 г. Всеволожск

Вариант№1

Зачет.8класс (4;5)

Вариант№1

Зачет.8класс (3;4)

Вариант№2

Зачет.8класс (4;5)

Вариант№2

Зачет.8класс (3;4)

Вариант№3

Зачет.8класс (4;5)

Вариант№3

Зачет.8класс (3;4)

Содержимое разработки

Содержимое разработки

Содержимое разработки

Получите свидетельство о публикации сразу после загрузки работы

Серия олимпиад «Осень 2024»

Комплекты учителю

Вебинары для учителей